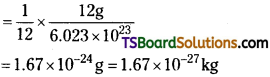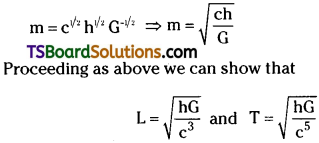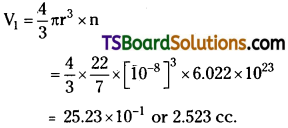TS Inter 1st Year

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 9 Differentiation will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Differentiation Formulas

→ Formula for finding derivative f'(x) of a function y = f(x) using the definition is
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = f'(x) = \({Lt}_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
Derivative of a function at a point ‘a’ f'(a) = \({Lt}_{x \rightarrow a}\left[\frac{f(x)-f(a)}{x-a}\right]\)

→ \(\frac{\mathrm{d}}{\mathrm{dx}}\)(u ± v) = \(\frac{d u}{d x} \pm \frac{d v}{d x}\)

→ \(\frac{d}{d x}\)(uv) = u.\(\frac{d v}{d x}\) + v.\(\frac{d u}{d x}\)

→ \(\frac{d}{d x}\) (uvw) = uv \(\frac{d}{d x}\)(w) + uw\(\frac{d}{d x}\)(v) + vw\(\frac{d}{d x}\)(u)

→ \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)

→ \(\frac{d}{d x}\)(xn) = n.x^n-1

→ \(\frac{d}{d x}\left(\frac{1}{x^n}\right)=\frac{-n}{x^{n+1}}\)

→ \(\frac{d}{d x}\)(log x) = \(\frac{1}{x}\), \(\frac{d}{d x}\)(log_a x) = log_a e

→ \(\frac{d}{d x}\)(e^x) = e^x, \(\frac{d}{d x}\)(a^x) = a^x log_e a

→ \(\frac{d}{d x}\)(sin x) = cos x

→ \(\frac{d}{d x}\)(cos x) = -sin x

→ \(\frac{d}{d x}\)(tan x) = sec² x

→ \(\frac{d}{d x}\)(cot x) = -cosec² x

→ \(\frac{d}{d x}\)(sec x) = sec x tan x

→ \(\frac{d}{d x}\)(cosec x) = -cosec x cot x

→ \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^2}}\)

→ \(\frac{d}{d x}\)(cos^-1x) = \(-\frac{1}{\sqrt{1-x^2}}\)

→ \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^2}\)

→ \(\frac{d}{d x}\)(cot^-1x) = \(-\frac{1}{1+x^2}\)

→ \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{|x| \sqrt{x^2-1}}\)

→ \(\frac{d}{d x}\)(cosec^-1x) = \(-\frac{1}{|x| \sqrt{x^2-1}}\)

→ \(\frac{d}{d x}\)(sinh^-1x) = \(\frac{1}{\sqrt{1+x^2}}\)

→ \(\frac{d}{d x}\)(cosh^-1x) = \(\frac{1}{\sqrt{x^2-1}}\)

→ \(\frac{d}{d x}\)(tanh^-1x) = \(\frac{-1}{1-x^2}\)

→ \(\frac{d}{d x}\)(coth^-1x) = \(\frac{1}{1-x^2}\)

→ \(\frac{d}{d x}\)(sech^-1x) = \(-\frac{1}{|x| \sqrt{1-x^2}}\)

→ \(\frac{d}{d x}\)(cosech^-1x) = \(\frac{1}{|x| \sqrt{x^2+1}}\)

→ Logarithmic differentiation: If y = f(x)^g(x) > then log y = g(x) log f(x)
⇒ \(\frac{1}{y} \frac{d y}{d x}\) = g(x).\(\frac{1}{f(x)}\)f'(x) + log[f(x)]g'(x)

→ Derivative of one function w.r.t. another function: If y = f(x); z = g(x) then \(\frac{d y}{d z}=\frac{d f}{d g}=\frac{f^{\prime}(x)}{g^{\prime}(x)}\), It is called as chain rule.

→ Parametric differentiation: If x = f(t), y = g(t) then \(\frac{d y}{d x}=\frac{d y}{\frac{d t}{d t}}=\frac{g^{\prime}(t)}{f^{\prime}(t)}\), Itis called as chain rule.
\(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(\frac{d y}{d x}\right)=\left[\frac{d}{d t}\left(\frac{d y}{d x}\right)\right]\left(\frac{d t}{d x}\right)\)

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 8 Limits and Continuity will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Limits and Continuity Formulas

→ If a variable x approaches a value a’ from the left i.e., through values just smaller than ’a’ than the limit of f defined is called the left limit of f(x) denoted by \(\lim _{x \rightarrow a^{-}}\)f(x)
\(\lim _{x \rightarrow a^{-}}\)f(x)= \(\lim _{h \rightarrow 0^{+}}\)f(a – h) = \(\lim _{x \rightarrow 0}\)f(a – x) (∵ x → a^– ⇒ x < a)

→ If x approaches a’ from the right i.e., through the values just greater than ‘a’ then the limit of f defined is called the right limit of f(x) denoted by \(\lim _{x \rightarrow a^{+}}\)(x).
\(\lim _{x \rightarrow a^{+}}\) f(x)= \(\lim _{h \rightarrow 0^{+}}\) f(a + h)= \(\lim _{x \rightarrow 0}\)f(a + x) (∵ x → a⁺ ⇒ x > a)

→ Suppose f is defined in a deleted neighbourhood of ‘a’ and l e R then
\(\lim _{x \rightarrow a}\)f(x) = l ⇒ \(\lim _{x \rightarrow a^{+}}\)f(x) = \(\lim _{x \rightarrow a^{-}}\)f(x) = l

→ Standard limits:

• \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}\) = na^n-1 and \(\lim _{x \rightarrow a}\left(\frac{x^m-a^m}{x^n-a^n}\right)=\frac{m}{n}\)a^m-n
• \(\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)\) = 1, \(\lim _{x \rightarrow 0}\left(\frac{\tan x}{x}\right)\) = 1
• \(\lim _{x \rightarrow 0}\left(\frac{a^x-1}{x}\right)\) = log_e^a
• \(\lim _{x \rightarrow 0}\)(1 + x)^{\(\frac{1}{x}\)} = e and \(\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x\) = e
• \(\lim _{x \rightarrow 0}\left(\frac{e^x-1}{x}\right)\) = 1

Note:
For finding \(\lim _{x \rightarrow a}\)f(x), first verify f(a). If this is in indeterminate form like \(\frac{0}{0}, \frac{\infty}{\infty}\) etc., then reduce the given limit into standard form or rationalise numerator or denominator or factorise according to the problem.

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 7 The Plane will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B The Plane Formulas

→ A plane is a proper subset of R’* which has atleast three non-collinear points and is such that for any two points in it. the line joining them also lies in it.

→ The general equation of a plane in the first degree equation in x, y, z given by ax + by + cz + d = 0. the coefficients a, b, c represent direction ratios of normal to the plane.

→ The equation of a plane passing through (x₁, y₁, z₁) and perpendicular to the line with direction ratios a, b, c is a (x – x₁) + b (y – y₁) + c (z – z₁) = 0.

→ Normal form of the plane is lx + my + nz – p where /. rn. n are direction cosine’s of normal and p is the perpendicular distance from origin to the plane.

→ The perpendicular distance from (0, 0, 0) to ax + by + cz t d = 0 is \(\frac{|d|}{\sqrt{a^2+b^2+c^2}\)

→ The perpendicular distance from A (x₁, y₁, z₁) to the plane ax + by + cz + d = 0 is \(\frac{\left|a x_1+b y_1+c z_1+d\right|}{\sqrt{a^2+b^2+c^2}}\)

→ The distance between parallel planes ax + by + cz + d₁ = 0 and ax + by + cz + d₂ = 0 is \(\frac{\left|d_1-d_2\right|}{\sqrt{a^2+b^2+c^2}}\)

→ The equation of plane with x. y. z intercepts a. b. c is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1.

→ The equation of the plane passing through 3 non-collinear points A (x₁, y₁ z₁). B (x₂, y₂, z₂) and C (x₃, y₃ z₃) is \(\left|\begin{array}{ccc}
x-x_1 & y-y_1 & z-z_1 \\
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
x_3-x_1 & y_3-y_1 & z_3-z_1
\end{array}\right|\) = 0

→ If θ is the angle between planes a₁x + b₁y + c₁z – d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 then cos θ = \(\)

→ The planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y – c₂z + d = 0 are parallel if \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) and perpendicular if a₁a₂ + b₁b₂ + c₁c₂ = 0.

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 6 Direction Cosines and Direction Ratios will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Formulas

→ If a line makes angles a, [3. y with the coordinate axes then cos α, cos β, cos γ are called ‘the direction cosines of the lines denoted by l, m, n.
The relation between l, in. n is l² + m² + n² = 1

→ An ordered triple of numbers proportional to the direction cosines of a line are called as direction ratios of the line.

→ If a, b, c are the dirrc!ion ratios of a ray then the direction cosine are given by \(\left(\frac{a}{\sqrt{a^2+b^2}+c^2} \cdot \frac{b}{\sqrt{a^2+b^2+c^2}}, \frac{c}{\sqrt{a^2+b^2}+c^2}\right)\)

→ Direction ratios of the line joining A (x₁, y₁, z₂) and B (x₂, y₂, z₂) are (x₂ – x₁, y₂ – y₁, z₂ – z₁) (or) (x₁ – x₂, y₁ – y₂, z₁ – z₂)

→ Direction cosines of the above line = \(\left(\frac{x_2-x_1}{A B}, \frac{y_2-y_1}{A B}, \frac{z_2-z_1}{A B}\right)\)

→ If θ is the angle between two lines with direction ratio’s (a₁, b₁, c₁) and (a₂, b₂, c₂) then
cos θ = \(\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{\left(a_1^2+b_1^2+c_1^2\right)\left(a_2^2+b_2^2+c_2^2\right)}}\)

→ If the above lines are perpendicular then a₁a₂ + b₁b₂ + c₁c₂ = 0.

→ In terms of direction cosine’s cos θ = l₁l₂ + m₁m₂ + n₁n₂, and for perpendicular lines l₁l₂ + m₁m₂ + n₁n₂ = 0.

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 5 Three Dimensional Coordinates will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates Formulas

→ Perpendicular distances front the point P(x, y, z ) to yz, zx and xy planes are |x|, |y|, |z|.

→ The distance between points A (x₁, y₁, z₁), B (x₂, y₂, z₂) is AB = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2+\left(z_1-z_2\right)^2}\)

→ The coordinates of a point which divides A = (x₁, y₁, z₁) and B = (x₂, y₂, z₂) internally in the ratio m₁ m₂ is = \(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}, \frac{m_1 z_2+m_2 z_1}{m_1+m_2}\right)\)

→ Coordinates of midpoint of a line segment AB joining
A = (x₁, y₁, z₁) and B = (x₂, y₂, z₂) is = \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2}{2}, \frac{\mathrm{y}_1+\mathrm{y}_2}{2}, \frac{\mathrm{z}_1+\mathrm{z}_2}{2}\right)\).

→ The centroid of the triangle formed by the points A (x₁, y₁, z₁) , B (x₂, y₂, z₂), C(x₃, y₃, z₃) is
G = \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2+\mathrm{x}_3}{3}, \frac{\mathrm{y}_1+\mathrm{y}_2+\mathrm{y}_3}{3}, \frac{\mathrm{z}_1+\mathrm{z}_2+\mathrm{z}_3}{3}\right)\)

→ The centroid of the tetrahedron formed by (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) and (x₄, y₄, z₄) is
G = \(\left(\frac{x_1+x_2+x_3+x_4}{4}, \frac{y_1+y_2+y_3+y_4}{4}, \frac{z_1+z_2+z_3+z_4}{4}\right)\)

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 4 Pair of Straight Lines will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Pair of Straight Lines Formulas

→ If a b and h are not all zero then the equation H ≡ ax² + 2hxy + by² = 0 represents a pair of straight lines if and only if h² ≥ ab.

→ If ax² + 2hxy + by² = 0 represent a pair of lines passing through the origin then the sum of the slopes of lines is \(\frac{-2h}{b}\) and product of the slopes is \(\frac{a}{b}\).
i.e.., if ax² + 2hxy + by² = (y – m₁x) (y – m₂x) then m₁ + m₂ = \(\frac{-2h}{b}\) and m₁ m₂ = \(\frac{a}{b}\).

→ If θ is the angle between the lines represented by ax² + 2hxy + ² = 0 then
cos θ = \(\frac{a+b}{\sqrt{(a-b)^2+4 h^2}}\) and tan θ = \(\frac{2 \sqrt{\mathrm{h}^2-a b}}{a+b}\)

• If h² = ab then ax² + 2hxy + by² = 0 represents coincident or parallel lines.
• ax² + 2hxy + by² = 0 represents a pair of perpendicular lines ⇔ a + b = 0 i.e., coefficient of x² + coefficient of y² = 0.

→ (i) The equation of pair < >f lines passing! Iirough origin and perpendicular to ax² + 2hxy + by² = 0 is bx² – 2hxy + ay² = 0,
(ii) The equation of pair of lines passing through (x₁, y₁) and perpendicular to ax² + 2hxy + by² = 0 is b(x – x₁)² – 2h (x – x₁) (y – y₁) – a(y – y₁)² = 0.
(iii) The equation of pair of lines passing through (x₁, y₁) and parallel to ax² + 2hxy + by² = 0 is a(x – x₁)²+ 2h (x – x₁) (y – y₁) + b(y – y₁)² = 0.

→ The equation of bisectors of angles between the lines a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 is \(\frac{a_1 x+b_1 y+c_1}{\sqrt{a_1^2+b_1^2}}\) = \(\frac{(a_2 x+b_2 y+c_2)}{\sqrt{a_2^2+b_2^2}}\)

→ The equation to the pair of bisectors of angles between the pair of lines ax² + 2hxy + by² = 0 is h(x² – y²) – (a – b)xy

→ The area of the triangle formed by ax² + 2hxy + by² = 0 and lx + my + n = 0 is \(\frac{n^2 \sqrt{h^2-a b}}{\left|a m^2-2 h l m+b l^2\right|}\)

→ The product of the perpendiculars from (α, β) to the pair of lines ax² + 2hxy + by² = 0 is \(\frac{\left|a \alpha^2+2 h \alpha \beta+b \beta^2\right|}{\sqrt{(a-b)^2+4 h^2}}\)

→ The line ax + by + c – 0 and pair of lines (ax + by)² – 3(bx – ay)² = 0 form an equilateral triangle and the area is \(\frac{c^2}{\sqrt{3}\left(a^2+b^2\right)}\) units

→ If S = ax² + 2hxy + by² + 2gx + 2fy + c = 0 represent the equation of pair of lines then

• Δ = abc + 2fgh – af² – bg² – ch² = 0
• h² ≥ ab, g² ≥ ac, f² ≥ be

→ The point of intersection of the pair of lines S ≡ 0 is \(\left(\frac{h f-b g}{a b-h^2}, \frac{g h-a f}{a b-h^2}\right)\)

→ If S ≡ ax² + 2hxy + by² + 2gx + 2fy + c = 0 represent a pair of parallel lines then

• h² = ab
• bg² = af²
• distance between them is 2\(\sqrt{\frac{g^2-a c}{a(a+b)}}\) (or) 2\(\sqrt{\frac{f^2-b c}{a(a+b)}}\)

→ The equation to the pair of lines joinmg the ongin to the points of intersection of the curve ax² + 2hxy + by² + 2gx + 2fy + c = 0 and the line lx + my + n = 0 is obtained by homogenisation ax² + 2hxy + by² + 2gx\(\left(\frac{l x+m y}{-n}\right)\) + 2fy\(\left(\frac{l x+m y}{-n}\right)\) + c\(\left(\frac{l x+m y}{-n}\right)^2\) = 0

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 3 The Straight Lines will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B The Straight Lines Formulas

→ The equation of a horizontal line which is parallel to X – axis and at a distance of k’ from X – axis and lying above X – axis is given by y = k.

→ Similarly, y = -k is the equation of the horizontal line which is at a distance of k from X – axis and lying below X -axis.

→ The equation of X – axis is y = 0.

→ The equation of a vertical line which is parallel to Y – axis and at a distance of k from Y – axis and lying left of Y – axis is x = k.

→ Similarly, x = -k is the equation of the vertical line which is at a distance of k units from Y – axis and lying right of Y – axis is x = -k.

→ Equation of Y- axis is x = 0.

→ If a non vertical straight line L makes an angle θ with X – axis measured anti-clockwise from the positive direction of the X – axis then tan θ is called the slope or gradient of the line L denoted by ‘m’.

→ Slope of horizontal line is 0 since tan 0 – 0 and slope of vertical line is not defined.

→ If m₁, m₂, are slopes of two lines and θ is called the angle between them then tan θ = \(\left(\frac{m_1-m_2}{1+m_1 m_2}\right)\)

→ If two lines are parallel then slopes are equal, m₁ = m₂, and if two lines are perpendicular then m₁. m₁ = -1.

→ Equation of a line passing through (x₁; y₁) with slope m’ is y – y₁ = m (x – x₁).

→ Equation of a line passing through origin with slope in is y = mx.

→ Equation of a line passing through the points A (x₁, y₁) and B (x₂, y₂) is \(\frac{y-y_1}{y_1-y_2}=\frac{x-x_1}{x_1-x_2}\)

→ Equation of a line with Y – intercept ‘c’ and slope m is y = mx + c.

→ Equation of a line in intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1.

→ Reduction of a straight line ax + by + c = 0 in intercept form is \(\frac{x}{-\left(\frac{c}{a}\right)}+\frac{y}{-\left(\frac{c}{b}\right)}\) = 1

→ Area of the triangle formed by the line ax + by + c = 0 with coordinate axes is \(\frac{c^2}{2|a b|}\).

→ Equation of a line in normal form or perpendicular form is x cos α + y sin α = p where p is the length of the perpendicular from origin to line and a. is the angle made by the perpendicular with + ve X – axis.

→ Reduction of the equation ax + by + c = 0 of a line to the normal form is \(\pm\left(\frac{a}{\sqrt{a^2+b^2}}\right) x+\left(\pm \frac{b}{\sqrt{a^2+b^2}}\right)=\frac{\pm c}{\sqrt{a^2+b^2}}\)

→ Perpendicular distance from (x₁; y₁) to the line ax + by + c = 0 is \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)

→ Perpendicular distance from origin to the line ax + by + c = 0 is points A (x₁, y₁) and B (x₂, y₂) is \(\frac{|c|}{\sqrt{a^2+b^2}}\)

→ The ratio in which the line L = ax + by + c = 0 (ab ≠ 0) divides the line segment AB joining points A(x₁, y₁) and B(x₂, y₂) is \(-\left(\frac{a x_1+b y_1+c}{a x_2+b y_2+c}\right)=-\frac{L_{11}}{L_{22}}\)
If L₁₁ and L₂₂ are having same sign or opposite sign then the points on same side or opposite sides of the line L = 0.

→ If (h, k) is the foot of the perpendicular from (x₁, y₁) to the line ax + by + c = 0. then \(\frac{h-x_1}{a}=\frac{k-y_1}{b}=-\left(\frac{a x_1+b y_1+c}{a^2+b^2}\right)\)

→ If (h, k) is the image of the point (x₁, y₁) with respect to the line ax + by + c = 0, then \(\frac{h-x_1}{a}=\frac{k-y_1}{b}=-2\left(\frac{a x_1+b y_1+c}{a^2+b^2}\right)\)

→ The point of intersection of lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 is \(\left(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}, \frac{c_1 a_2-a_1 c_2}{a_1 b_2-a_2 b_1}\right)\)

→ If angle between lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 is 0 where (0 ≤ θ ≤ π), then
cos θ = \(\frac{a_1 a_2+b_1 b_2}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
sin θ = \(\frac{a_1 b_2-a_2 b_1}{\sqrt{a_1^2+b_1^2} \sqrt{a_2^2+b_2^2}}\)
and tan θ = \(\frac{a_1 b_2-a_2 b_1}{a_1 a_2+b_1 b_2}\)

• Lines are perpendicular ⇔ a₁a₂ + b₁b₂ = 0
• Lines are parallel ⇔ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)

→ The equation of a line passing through (x₁, y₁) and parallel to the line ax + by + c = 0 is a (x – x₁) – b (y – y₁) = 0.

→ The equation of a line passing through (x₁, y₁) and perpendicular to ax + by + c = 0 is b(x – x₁) – a(y – y₁) = 0.

→ If a₁x + b₁y + c₁ = 0. a₂x + b₂y + c₂ = 0, and a₃x + b₃y + c₃ = 0 represent three lines, no two of which are parallel, then a necessary and sufficient condition for these lines to be concurrent is Σa₁(b₂c₃ – b₃c₂) = 0 (0r) \(\left|\begin{array}{lll}
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right|\) = 0

→ The distance between parallel lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 is \(\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}\)

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 2 Transformation of Axes will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Transformation of Axes Formulas

→ The transformation obtained, by shifting the origin to a given different point in the plane without changing the directions of coordinate axes therein is called a Translation of axes.
If the origin is shifted to (h, k) by translation of axes, then

• The coordinates of a point P(x, y) are transformed as P(x – h, y – k) and
• The equation f(x, y) = 0 of the curve is transformed as f(X + h. Y + k) = 0

→ The transformation obtained, by rotating both the coordinate axes in the plane by an equal angle, without changing the position of the origin is called a Rotation of axes.
x = X cos θ – Y sin θ, X = x cos θ – y sin θ
y = X sin θ + Y cos θ, Y = – x sin θ + y cos θ

→ To make the first degree terms absent, origin should be shifted to \(\left(\frac{h f-b g}{a b-h^2}, \frac{g h-a f}{a b-h^2}\right)\)

→ To make xy term to be absent, axes should be rotated through an angle 0 given by tan 2θ = \(\frac{2 h}{a-b}\)
⇒ θ = \(\frac{1}{2}\)tan^-1\(\left(\frac{2 h}{a-b}\right)\)

Learning these TS Inter 1st Year Maths 1B Formulas Chapter 1 Locus will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1B Locus Formulas

→ Consider a pair of mutually perpendicular lines of reference X’ X, Y’ Y in a plane. These are called the coordinate axes and their point of intersection is called the origin denoted by ‘O’.

→ Consider a point P in the plane. Let x, denotes the perpendicular distance of P from Y – axis and yx denotes the perpendicular distance of P from X – axis. Then P is represented as ordered pair in the following quadrants.
1st Quadrant → P (x₁, y₁)
2ndQuadrant → P(-x₁, y₁)
3rd Quadrant → P (- x₁, – y₁)
4th Quadrant → P(x₁, -y₁)
The first element is called the x – coordinate (abscissa) and the second element is called the y- coordinate (ordinate).

• The distance between the points P(x₁, y₁) and Q(x₂, y₂) in the plane denoted by
  PQ = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{(\text { difference of } x \text {-coordinates })^2+(\text { difference of } y \text {-coordinates })^2}\)
• The distance of P(x₁, y₁) from the origin (0, 0) is OP = \(\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2}\)
• The distance between [joints A (x₁, 0) and B (x₂,0) is AB = \(\sqrt{\left(x_1-x_2\right)^2+(0-0)^2}\) = (x₁ – x₂).
• The distance between points A (0, y₁) and B (0, y₂) is y₁ – y₂.

→ Section Formulae:

• The coordinates of the point ‘P’ which divides the line segment joining points A(x₁, y₁) and B(x₂, y₂) internally in the ratio m₁ : m₂ is \(\left(\frac{m_1 x_2+m_2 x_1}{m_1+m_2}, \frac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)\)
• The coordinates of the point P’ which divides the line segment joining points A(x₂, y₂) and B(x₂, y₂)Externally in the ratio m₁ : m₂ is \(\left(\frac{m_1 x_2-m_2 x_1}{m_1-m_2}, \frac{m_1 y_2-m_2 y_1}{m_1-m_2}\right)\)
• Coordinates of midpoint of the line segment \(\overline{\mathrm{AB}}\) is \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
• The points which divide a line segment in the ratio 1 : 2 or 2 : 1 are called the points of trisection.

→ (i) The area of the triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) is given by
Δ = \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁)+ x₃(y₁ – y₂) = \(\frac{1}{2}\)Σx₁(y₂ – y₃)
(ii) The area of the triangle OAB with vertices O (0, 0), A(x₁, y₁) and B(x₂, y₂) is given by
Δ = \(\frac{1}{2}\)|x₁y₂ – x₂y₁|

→ The area of the quadrilateral with vertices A(x₁, y₁), B(x₂, y₂) C(x₃, y₃) and D(x₄, y₄) is
= \(\frac{1}{2}\)|x₁(y₂ – y₄) + x₂(y₃ – y₁) + x₃(y₄ – y₂) + x₄(y₁ – y₃) = \(\frac{1}{2}\)Σx₁(y₂ – y₄)

→ In a triangle the line segment joining a vertex to the midpoint of opposite side is called the median. Point of intersection of the 3 medians of the triangle is called the centroid of the triangle denoted by G. This point G divides every median internally in the ratio 2 : 1.

→ The coordinates of centroid of the triangle having vertices A (x₁, y₁), B ( x₂, y₂) and C (x₃, y₃) is G = \(\)

→ The bisectors of internal angles of a triangle are concurrent and the point of concurrence is called in center of the triangle denoted by 1.
This is equidistant from three sides and this distance is called the in radius denoted by r. The circle drawn with I as centre and r as radius touches all the three sides internally and this circle is called the in- circle.

→ If A (x₁, y₁), B ( x₂, y₂) and C (x₃, y₃) are the vertices and a,b, and c are respectively the sides BC, CA and AB of triangle ABC, then the coordinates of the in center are
I = \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

→ In a triangle, one internal angular bisector and two externa! angular bisectors are concurrent j and the point of concurrence is called the Ex-centre of the triangie denoted by I₁.
This is equidistant from one side and extensions of the other sides. This distance is called i the Ex-radius of the lriangie denoted by r₁. The circle drawn with I₁ as centre and r₁ as radius touches these sides. This circle is called the Ex-circle of the triangle opposite to the vertex A. Similarly we have two more centres I₂ and I₃ with radii r₂ r₃. Coordinates of ex-centres of the triangle are given by
I₁ = \(\left(\frac{-a x_1+b x_2+c x_3}{-a+b+c}, \frac{-a y_1+b y_2+c y_3}{-a+b+c}\right)\)
I₂ = \(\left(\frac{a x_1-b x_2+c x_3}{a-b+c}, \frac{a y_1-b y_2+c y_3}{a-b+c}\right)\)
I₃ = \(\left(\frac{a x_1+b x_2-c x_3}{a+b-c}, \frac{a y_1+b y_2-c y_3}{a+b-c}\right)\)
where A (x₁, y₁), B ( x₂, y₂), C (x₃, y₃) are vertices of the triangle.

→ A set of geometric conditions is said to be consistent if there exists atleast one point satisfying the set of conditions. As an example, if A = (1, 0) and B = (3, 0) then PA + PB = 2 represents the sum of the distances of a point P from A and B is equal to 2, is a consistent condition whereas the distances of a point Q from A and B. ie., QA + QB = 1 is not consistent (∵ AB = 2).

→ Locus is the set of points (and only those points) that satisfy the given consistent geometric conditions. Hence

• Every point satisfying the given condition (s) is a point on the locus.
• Every point on the locus satisfies the given conditions).

→ Equation of locus of a point is an algebraic equation in ‘x’ and y’ satisfied by the points (x, y) on the locus alone. To get the full description of the locus, the exact part of the curve, the points of which satisfy the given geometric description need to be specified.

Telangana TSBIE TS Inter 1st Year Physics Study Material 2nd Lesson Units and Measurements Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 2nd Lesson Units and Measurements

Very Short Answer Type Questions

Question 1.
Distinguish between accuracy and precision. [AP Mar. ’15, ’16, May 16, 13, June 15; TS May ’18, Mar. ’15]
Answer:
Accuracy :
It indicates the closeness of a measurement to the true value of given quantity.
→ If the measurement is nearer to true value then accuracy is more.

Precision :
Precision of a measuring instrument depends on the limit (or) resolution of the quantity measured with that instrument.
→ If the least measurable value is less, then precision is more for that instrument.

Question 2.
What are the different types of errors that can occur in a measurement?
Answer:
Types of errors 1) Systematic errors and 2) Random errors.

Systematic errors are again divided into 1) Imperfectional errors 2) Environmental errors and 3) Personal errors.

Question 3.
How can systematic errors be minimised or eliminated? [AP May ’17; TS Mar. ’17; AP May ’17; TS Mar. ’17]
Answer:
Systematic errors can be minimised

1. by improving experimental techniques,
2. by selecting better instruments,
3. by taking mean value of number of readings and
4. by removing personal errors as far as possible.

Question 4.
Illustrate how the result of a measurement is to be reported indicating the error involved.
Answer:
Suppose length of an object is measured with a metre rod with least count equal to 0.1 cm. If the measured length is 62.5 cm, it has to be recorded as (62.5 ± 0.1) cm, stating the limits of error. Similarly, suppose time period of a pendulum is measured to be 2.0 sec, using a stopwatch of least count 0.1 sec, it has to be recorded as (2.0 ± 0.1) sec. It indicates that time period is in the range of 1.9 sec and 2.1 sec.

Question 5.
What are significant figures and what do they represent when reporting the result of a measurement? [TS Mar. ’18]
Answer:
Significant figures represents all practically measured digits plus one uncertain digit at the end.

When a result is reported in this way we can know up to what extent the value is reliable and also the amount of uncertainty in that reported value.

Question 6.
Distinguish between fundamental units and derived units. [TS Mar. ’16 ; AP May ’14]
Answer:
1) Fundamental units are used to measure fundamental quantities. Derived units are used to measure derived quantities.

2) Fundamental units are independent. Derived units are obtained by the combination of Fundamental units.
Ex: Metre is fundamental unit of length L’. metre/sec is derived unit of velocity which is a combination of fundamental unit metre and second.

Question 7.
Why do we have different units for the same physical quantity? [TS May ’16. June ’15]
Answer:
To measure the same physical quantity we have different units by keeping magnitude of the quantity to be measured.
Example:

1. The measure astronomical distances we will use light year.
   1 light year = 9.468 × 10¹⁵m.
2. To measure atomic distances we will use Angstrom A (or) Fermi.

Question 8.
What is dimensional analysis?
Answer:
Dimensional analysis is a tool to check the relations among physical quantities by using their dimensions.
Dimensional analysis is generally used to check the correctness of derived equations.

Question 9.
How many orders of magnitude greater is the radius of the atom as compared to that of the nucleus?
Answer:
Size of atom = 10^-10 m,
Size of atomic nucleus = 10^-14m.
Size of atom ÷ size of nucleus is \(\frac{10^{-10}}{10^{-14}}\) = 10⁴
∴ Size of atom is 10⁴ times greater than size of nucleus.

Question 10.
Express unified atomic mass unit in kg. [TS Mar. ’19]
Answer:
By definition,
1 a.m.u. = \(\frac{1}{12}\) × mass of an atom of ¹²₆C

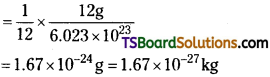
Short Answer Questions

Question 1.
The vernier scale of an instrument has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm, then using this instrument what would be the minimum inaccuracy in the measurement of distance?
Answer:
Least count of Vernier Callipers = 1 MSD – 1 VSD
∴ L.C. = 1 MSD – \(\frac{49}{50}\)MSD = \(\frac{1}{50}\)MSD
= \(\frac{1}{50}\) × 0.5 = 0.01 m.m

Question 2.
In a system of units, the unit of force is 100N, unit of length is 10m and the unit of time is 100s. What is the unit of mass in this system?
Answer:
Here, F = MLT^-2 = 100 N → (1) ;
L = 10 m ; T = 100s
∴ From equation (1)
M × (10) × (100)^-2 = 100 ⇒ M × 10^-3 = 100
⇒ M = \(\frac{100}{10^{-3}}\) ⇒ M = 10⁵ kg.

Question 3.
The distance of a galaxy from Earth is of the order of 10²⁵m. Calculate the order of magnitude of the time taken by light to reach us from the galaxy.
Answer:
Size of galaxy = 10²⁵m,
Velocity of light, c = 3 × 10⁸ ms^-1
Time taken by light to reach earth,

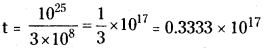
While calculating the order of magnitude we will consider the powers of Ten only.
So order of magnitude of time taken by light to reach earth from galaxy is 1017 seconds.

Question 4.
The Earth-Moon distance is about 60 Earth radius. What will be the approximate diameter of the Earth as seen from the Moon?
Answer:
Earth moon distance, D = 60r.
Diameter of earth, b = 2r

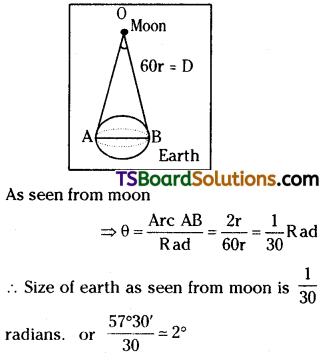
Question 5.
Three measurements of the time for 20 oscillations of a pendulum give t₁ = 39.6 s, t₂ = 39.9 s and t₃ = 39.5 s. What is the precision in the measurements? What is the accuracy of the measurements?
Answer:
Precision is the least measurable value with that instrument in our case precision is ±0.1 sec.

Calculation of accuracy :
Average value of measurements

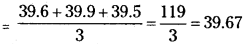
Error in each measurement =

Precision ± 1 sec. In these measurements only two significant figures are believable. 3rd one is uncertain.

Adjustment of ∆a_mean upto given significant figure = 0.156 adjusted to 0.2.

So our value is accurate upto ±0.2

So our result is 39.67 ± 0.2, when significant figures taken into account it is 39.7 ± 0.2 sec.

Question 6.
1 calorie = 4.2 J where 1J = 1 kg m²s^-2. Suppose we employ a system of units in which the unit of mass is α kg, the unit of length is β m and the unit of time γ s, show that a calorie has a magnitude 4.2 α^-1 β^-2 γ² in the new system.
Answer:
Here, 1 calorie = 4.2 J = 4.2 kg m² / s² → (1)
As new unit of mass = α kg
∴ 1 kg = \(\frac{1}{\alpha}\) new unit of mass
⇒ α^-1 new unit of mass

Similarly lm = β^-1 new unit of length and 1s = γ^-1 new unit of time

Putting these values in (1) we get
1 calorie = 4.2 (α^-1 new unit of mass) (β^-1 new unit of length)² (γ^-1 new unit of time)^-2
= 4.2 α^-1 β^-2 γ² new unit of energy, which was proved.

Question 7.
A new unit of length is chosen so that the speed of light in vacuum is 1 ms^-2. If light takes 8 min and 20s to cover this distance, what is the distance between the Sun and Earth in terms of the new unit?
Answer:
Given that velocity of light in vacuum,
c = 1 new unit of length s^-1
Time taken by light of Sun to reach Earth, t = 8 min 20s = 8 × 60 + 20 = 500 s
∴ Distance between the Sun and Earth, x = c × t
= 1 new unit of length s^-1 × 500s
= 500 new units of length.

Question 8.
A student measures the thickness of a human hair using a microscope of magnification 100. He makes 20 observations and finds that the average thickness (as viewed in the microscope) is 3.5 mm. What is the estimate of the thickness of hair?
Answer:

∴ Thickness of hair is 0.035 mm

Question 9.
A physical quantity X is related to four mea-surable quantities a, b, c and d as follows:
X = a²b³C^5/2d^-2
The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4% respectively. What is the percentage error in X?
Answer:
Here, X = a²b³C^5/2d^-2

The percentage error in X is ± 23.5 %

Question 10.
The velocity of a body is given by v = At² + Bt + C. If v and t are expressed in SI, what are the units of A, B and C?
Answer:
From principle of Homogeneity the terms At², Bt and C must have same dimensional formula of velocity ‘v’.
v = Velocity = LT^-1 ⇒ CT^-1 = A [T²]
∴ A = \(\frac{LT^{-1}}{T^2}\) = LT^-3 . So unit of A is m/sec³
LT^-1 = BT ⇒ B = LT^-2 So unit of B is m/sec²
LT^-1 = C So unit of C is m/sec.

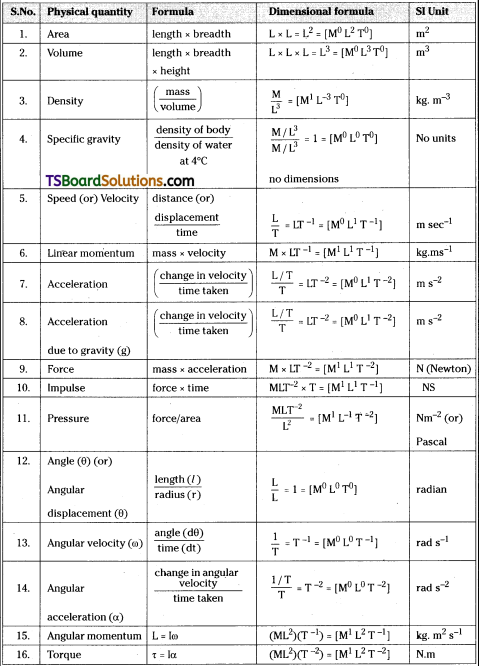
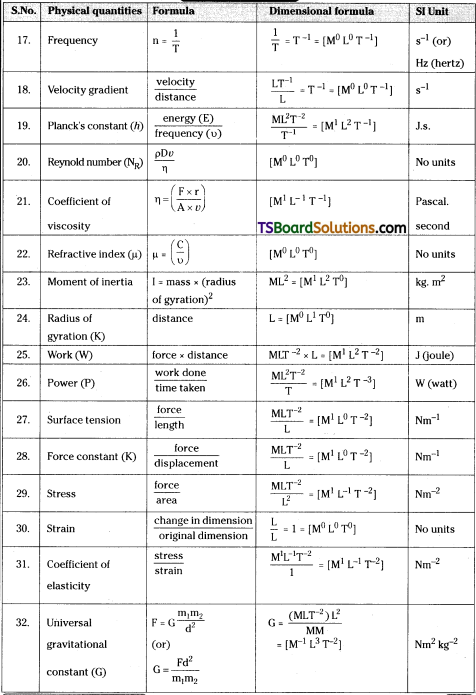
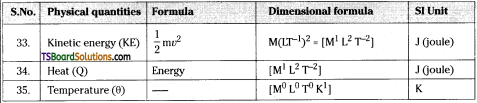
Dimensional formulae of physical quantities

Problems

Question 1.
In the expression P = El² m^-5 G^-2 the quantities E, l, m and G denote energy, angular momentum, mass and gravitational constant respectively. Show that P is a dimensionless, quantity.
Solution:
Here, P = El² m^-5 G^-2
Here,
I = energy,
l = angular momentum
m = mass
G = gravitational constant
= [M L²T^-2][ML²T^-1]² [M]^-5 [M^-1L³T^-2]^-2
= M^1+2+5+2 L^2+4-6 T^-2-2+4
P = [M° L° T°]
Hence, P is a dimensionless quantity.

Question 2.
If the velocity of light c, Planck’s constant, h and the gravitational constant G are taken as fundamental quantities; then express mass, length and time in terms of dimensions of these quantities.
Solution:
Here, c = [L T^-1] ; h = [ML²T^-1]
G = [M^-1L³T^-2]

Applying the principle of homogeneity of dimensions, we get

y – z = 1 → (2) ; x + 2y + 3z = 0 → (3) ; – x – y – 2z = 0 → (4)
Adding eq. (2), eq. (3) and eq. (4),
2y – 1 ⇒ y = \(\frac{1}{2}\)
∴ From eq. (2) z = y – 1 = \(\frac{1}{2}\) – 1 = \(\frac{-1}{2}\)
From eq. (4) x = -y – 2z = \(\frac{-1}{2}\) + 1 = \(\frac{1}{2}\)
Substituting the values of x, y & z in eq. (1), we get

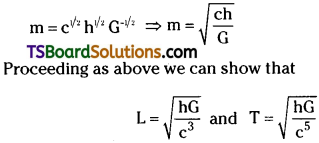
Question 3.
An artificial satellite is revolving around a planet of mass M and radius R, in a circular orbit of radius r. Using dimensional analysis show that the period of the satellite.
T = \(\frac{k}{R} \sqrt{\frac{r^3}{g}}\)
where k is a dimensionless constant and g is acceleration due to gravity.
Solution:
Given that
T² ∝ r³ or T ∝ r^3/2 Also T is a function of g and R
Let T ∝ r^3/2 g^a R^b where a, b are the dimen¬sions of g and R.
(or) T = k r^3/2 g^a R^b → (1)
where k is dimensionless constant of proportionality
From equation (1)

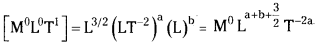
Applying the principle of homogeneity of dimensions, we get

a + b + \(\frac{3}{2}\) = 0 → (2) ∴ -2a = 1 ⇒ a = \(\frac{-1}{2}\)
From eq (1), \(\frac{-1}{2}\) + b + \(\frac{3}{2}\) = 0 ⇒ b = -1
Substituting the values of a’ and b’ in eq. (1), we get

This is the required relation.

Question 4.
State the number of significant figures in the following
a) 6729 b) 0.024 c) 0,08240 d) 6.032 e) 4.57 x 108
Solution:
a) In 6729 all are significant figures.
∴ Number of significant figures Four.

b) In 0.024 the zeroes to the left of 1st non-zero digit of a number less than one are not significant.
∴ Number of significant figures Two.

c) 0.08240 – Significant figures Four.

d) In 6.032 the zero between two non-zero digits is significant.
So, number of significant figures in 6.023 are 4.

e) 4.57 × 10⁸ – Significant figures Three. [In the representation of powers of Ten our rule is only significant figures must be given].

Question 5.
A stick has a length of 12.132 cm and another has a length of 12.4 cm. If the two sticks are placed end and to what is the total length? If the two sticks are placed side by side, what is the difference in their lengths?
Solution:
a) When placed end to end total length is l = l₁ + l₂
l₁ = 12.132 cm and l₂ = 12.4 cm.
∴ l₁ + l₂ = 12.132 + 12.4 = 24.532 cm.

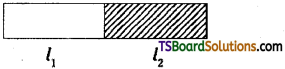
In addition final answer must have least number of significant numbers in that addition, i.e., one after decimal point.
So our answer is 24.5 cm. b) For difference use l₁ – l₂
i.e., 12.4- 12.132 = 0.268 cm.
In subtraction final answer must be adjusted to least number of significant figures in that operation.

Here least number is one digit after decimal. By applying round off procedure our answer is 0.3 cm.

Question 6.
Each side of a cube is measured to be 7.203 m. What is (i) the total surface area and (ii) the volume of the cube, to appropriate significant figures?
Solution:
Side of cube, a = 7.203 m.
So number of significant figures are Four.
i) Surface area of cube = 6a²
= 6x 7.203 × 7.203 = 311.299

But our final answer must be rounded to least number of significant figures is four digits.
So surface area of cube = 311.3 m²
ii) Volume of cube, V = a³ = (7.203)³
= 373.147
But the answer must be limited to Four significant figures.
∴ Volume of sphere, V = 373.1 m³.

Question 7.
The measured mass and volume of a body are 2.42 g and 4.7 cm³ respectively with possible errors 0.01 g and 0.1 cm³. Find the maximum error in density.
Solution:
Mass, m = 2.42 g ; Error, ∆m = 0.01 g.
Volume, V = 4.7 cm³, Error, ∆V = 0.1 cc.

Maximum % error in density = % error in mass + % error in volume Maximum percentage error in density
= \(\frac{1}{2.42}+\frac{10}{4.7}\) = 0.413 + 2.127 = 2.54%

Question 8.
The error in measurement of radius of a sphere is 1%. What is the error in the measurement of volume? [AP Mar. ’19]
Solution:

Question 9.
The percentage error in the mass and speed are 2% and 3% respectively. What is the maximum error in kinetic energy calculated using these quantities?
Solution:
Percentage change in mass = \(\frac{\Delta \mathrm{m}}{\mathrm{m}}\) × 100 = 2%

Question 10.
One mole of an ideal gas at standard temperature and pressure occupies 22.4 L (molar volume). If the size of the hydrogen molecule is about 1Å, what is the ratio of molar volume to the atomic volume of a mole of hydrogen?
Solution:
Size of Hydrogen atom ≈ 1Å = 10^-10 m = 10^-8cm
V₁ = Atomic volume = number of atoms × volume of atom.
One mole gas contains n’ molecules.
Avogadro Number, n = 6.022 × 10²³

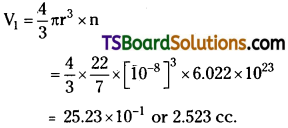
V₂ = Molar volume of 1 mol. gas = 22.4 lit
= 2.24 × 10⁴C.C
∵ 1 lit = 1000 c.c.
∴ Ratio of molar volume to atomic volume = V₂ : V₁
= 2.24 × 10⁴ : 2.523 ≅ 10⁴ m.

Telangana TSBIE TS Inter 1st Year Physics Study Material 1st Lesson Physical World Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 1st Lesson Physical World

Very Short Answer Type Questions

Question 1.
What is Physics? [TS Mar. ’16]
Answer:
Physics is a branch of science which deals with the study of nature and natural phenomena.

Question 2.
What is the discovery of C.V. Raman? [AP Mar. ’18, 14; May 18, 16, 14; TS Mar. ’19, ’18, ’17]
Answer:
C.V. Raman’s contribution to physics is Raman effect. It deals with scattering of light by molecules of a medium when they are excited to vibrational energy levels.

Question 3.
What are the fundamental forces in nature? [TS May ’18]
Answer:
There are four fundamental forces in nature that govern the diverse phenomena of the macroscopic and the microscopic wu.m. These are the ‘gravitational force’, the ‘electromagnetic force’, the ‘strong nuclear force’, and the ‘weak nuclear force’.

Question 4.
Which of the following has symr etry?
a) Acceleration due to gravity.
b) Law of gravitation.
Answer:
Acceleration due to gravity varies from place to place. So it has no symmetry.
Law of gravitation has symmetry, because it does not depend on any physical quantity.

Question 5.
What is the contribution of S. Chandra Sekhar to Physics?
Answer:
S. Chandra Sekhar discovered the structure and evolution of stars. He defined “Chandra Sekhar limit” which is used in the study of black holes.

Question 6.
What is beta (β) decay? Which force is a function of it?
Answer:
In β-decay the nucleus emits an electron and an uncharged particle called neutrino.

β – decay is due to weak nuclear forces.

❖ Some physicists and their major contributions

❖ Fundamental forces of nature

❖ Fundamental constants of Physics

❖ Conversion factors:
1 metre – 100 cm
1 millimeter – 10^-3m
1 inch – 2.54 × 10^-2m
1 micron (µ) – 10^-4cm
1 Angstrom (A°) – 10^-8cm
1 fermi (f) – 10^-13 cm
1 kilometer – 10³ m
1 light year – 9.46 × 1015 m
1 litre – 10³cm³
1 kilogram – 1000 gm
1 metricton – 1000 kg
1 pound – 453.6 gm
1 atomic mass
unit (a.m.u) 1.66 × 10^-27 kg
1 a.m.u – 931 MeV
1 day – 8.640 × 10⁴ seconds
1 km/hour – \(\frac{5}{18}\) m/sec (or)
0.2778 meter/sec.
1 Newton – 10⁵ dynes
1 gm wt – 980.7 dynes
1 kg.wt – 9.807 Newton
1 Newton/meter² – 1 pascal

1 Pascal – 10 dyne/cm²
1 Joule – 10⁷ erg
1 kilo watt hour – 3.6 × 10⁶ joule
1 electro volt (ev) – 1.602 × 10^-19 joule
1 watt – 1 joule / sec
1 horse power (HP) – 746 watt
1 degree (° ) – 60 minute (‘)
1 Radian – 57.3 degree ( ° )
1 Poise – 1 dyne . sec / cm²
1 Poiseuille – 10 poise
(Newton, sec/m² (or) Pascal sec.)

❖ Important Prefixes:

❖ The Greek Alphabet:

❖ Formulae of geometry :
1. Area of triangle = \(\frac{1}{2}\) × base × height
2. Area of parallelogram = base × height
3. Area of square = (length of one side)²
4. Area of rectangle = length × breadth
5. Area of circle = πr² (r = radius of circle)
6. Surface area of sphere = 4πr² (r = radius of sphere)
7. Volume of cube = (length of one side of cube)³
8. Volume of parallelopiped = length × breadth × height
9. Volume of cylinder = πr²l
10. Volume of sphere = \(\frac{4}{3}\)πr³
Circumference of square = 4l
11. Volume of cone = \(\frac{1}{3}\) πr²h
12. Circumference of circle = 2πr

❖ Formulae of algebra:
(a + b)² = a² + b² + 2ab
(a – b)² = a² + b² – 2ab
(a² – b²) = (a + b) (a – b)
(a + b)³ = a³ + b³ + 3ab (a + b)
(a – b)³ = a³ – b³ – 3ab (a – b)
(a + b)² – (a – b)² = 4ab
(a + b)² + (a – b)² = 2(a² + b²)

❖ Formulae of differentiation:
1. \(\frac{d}{dx}\) (constant) = 0
differentiation with respect to x = \(\frac{d}{dx}\)
2. \(\frac{d}{dx}\) (xⁿ) = n x^{n – 1}
3. \(\frac{d}{dx}\) (sin x) = cos x
4. \(\frac{d}{dx}\) (cos x) = – sin x dx

❖ Formulae of Integration:
Integration with respect to x = ∫dx
1. ∫dx = x
2. ∫xⁿ dx = r n + 1
3. ∫sin x dx = cos x + c
4. ∫cos x dx = sin x + c

❖ Formulae of logarithm :
1. log mn = (log m + log n)
2. log\(\frac{m}{n}\) = (log m – log n)
3. log mⁿ = n log m

❖ Value of trigonometric functions :

❖ Signs of trigonometrical ratios :
sin (90° – θ) = cos θ ; sin (180° – θ) = sin θ
cos (90° – θ) = sin θ ; cos (180° – θ) = – cos θ
tan (90° – θ) = cot θ ; tan (180° – θ) = – tan θ

❖ According to Binomial theorem :
(1 + x)ⁿ ≈ (1 + nx) if x < < 1

❖ Quadratic equation:
ax² + bx + c = 0

Learning these TS Inter 1st Year Maths 1A Formulas Chapter 5 Products of Vectors will help students to solve mathematical problems quickly.

TS Inter 1st Year Maths 1A Products of Vectors Formulas

→ The dot or scalar product of two vectors which are non zero denoted by a̅. b̅ and defineci by a̅. b̅ = |a̅| |b̅| cos θ where θ is the angle between a̅ and b̅ which is geometrically equal to product of magnitude of one of the vectors and the projection of the other on the first vector.

→ Dot product is a scalar, if a̅ = 0 or b̅ = 0 then wre define a̅ . b̅ = 0; If we write (a, b) = 9 then a̅ . b̅ = |a̅| |b̅| cos θ if a ≠ 0. b ≠ 0. a̅ .b̅ ⇔ a̅ and b̅ are perpendicular.

• Projection of b̅ on a̅ = \(\frac{|\bar{a} \cdot \bar{b}|}{|\bar{a}|}\)
• Orthogonal projection b̅ on a̅ = \(\frac{(\bar{a} \cdot \bar{b}) \bar{a}}{|\bar{a}|^2}\); a̅ ≠ 0
  (or) \(\left(\frac{\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}}{|\overline{\mathrm{a}}|^2}\right)\)a̅ and its magnitude = \(\frac{|\bar{a} \cdot \bar{b}|}{|\bar{a}|}\)
• Component vector of b̅ along a̅ (or) parallel to a̅ is \(\left(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^2}\right)\)a̅.
• Component vector of b̅ along a̅ (or) parallel to a̅ is \(\left(\frac{\bar{a} \cdot \bar{b}}{|\bar{b}|^2}\right)\) b̅ and component vector of a̅ perpendicular to b̅ is b̅ = a̅ – \(\frac{(\bar{a} \cdot \bar{b}) \bar{b}}{|\bar{b}|^2}\)

→ If i̅, j̅, k̅ are orthogonal unit vectors then i̅. j̅ = j̅.k̅ = k̅.i̅ = 0 and i̅ . i̅ = j̅ . j̅ = k̅ . k̅ = 1

→ If a̅, b̅, c̅ are any three vectors then

• (a̅ + b̅)² = |a̅|² + |b̅|² + 2(a̅ . b̅)
• (a̅ – b̅)² = |a̅|² – |b̅|² + 2(a̅ . b̅)
• (a̅ + b̅)² + (a̅ – b̅)² = 2(|a̅|² + |b̅|²)

→ If a̅ = a₁i̅ + a₂j̅ + a₃k̅ and b̅ = b₁i̅ + b₂j̅ + b₃k̅ then

• a̅.b̅ = a₁b₁ + a₂b₂ + a₃b₃
  a̅ is perpendicular to b̅ ⇔ a₁b₁ + a₂b₂ + a₃b₃ = 0
• cos θ = \(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}||\bar{b}|}=\frac{a_1 b_1+a_2 b_2+a_3 b_3}{\sqrt{\Sigma a_1^2} \sqrt{\Sigma b_1^2}}\)
• a̅ is parallel to b̅ ⇔ \(\frac{a_1}{b_1}=\frac{a_2}{b_2}=\frac{a_3}{b_3}\)
• a̅.a̅ ≥ 0; |a̅.b̅| ≤ |a̅||b̅|
  |a̅ + b̅| ≤ |a̅| + |b̅|; |a̅ – b̅| ≤ |a̅| + |b̅|

→ a̅ × b̅ = |a̅||b̅| sin θ n̂ is the vector product of two vectors a̅ and b̅ and n̂ is a unit vector perpendicular to the plane containing a̅ and b̅.
sin θ = \(\frac{|\bar{a} \times \bar{b}|}{|\bar{a}||\bar{b}|}\); n = \(\frac{\bar{a} \times \bar{b}}{|\bar{a} \times \bar{b}|}\)
Also a̅ × b̅ ≠ b̅ × a̅ and a̅ × b̅ = -(b̅ × a̅)

→ (i) a̅ × a̅ = 0̅ , a̅, b̅ are parallel ⇒ a̅ × b̅ = 0

• i̅ × i̅ = j̅ × j̅ = k̅ × k̅ = 0̅
• i̅ × j̅ = k̅; j̅ × k̅ = i̅ , k̅ × i̅ = j̅

(ii) If a̅ = a₁i̅ + a₂j̅ + a₃k̅, b̅ = b₁i̅ + b₂j̅ + b₃k̅ ⇒ a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
\mathrm{a}_1 & \mathrm{a}_2 & \mathrm{a}_3 \\
\mathrm{~b}_1 & \mathrm{~b}_2 & \mathrm{~b}_3
\end{array}\right|\)

→ (i) Vector area of parallelogram with adjacent sides a̅, b̅ = |a̅ x b̅|
(ii) Vector area of parallelogram with diagonals \(\overline{\mathrm{d}}_1, \overline{\mathrm{d}}_2=\frac{1}{2}\left|\overline{\mathrm{d}}_1 \times \overline{\mathrm{d}}_2\right|\)
(iii) Area of the quadrilateral with diagonals \(\overline{\mathrm{AC}}, \overline{\mathrm{BD}}=\frac{1}{2}|\overline{\mathrm{AC}} \times \overline{\mathrm{BD}}|\)
(iv) Area of ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)

→ The vector equation of a plane in the normal form is r̅.n̅ = p, where n̅ is a unit normal vector from the origin to the plane and p is the perpendicular distance from the origin to the plane.

→ The vector equation of a plane passing through the point A(a̅) and perpendicular to n̅ is (r̅ – a̅)n̅ = 0 or r̅.n̅ = a̅. n̅

→ The angle 0 between the planes r̅,n̅₁ = p₁ and r̅ . n̅₂ = p₂ is 0 = cos^-1\(\frac{\bar{n}_1 \cdot \bar{n}_2}{\left|\bar{n}_1\right|\left|\bar{n}_2\right|}\)

→ The scalar triple product (STP) of the vectors a,b, c is (a̅ × b̅) . c̅ or a̅ . (b̅ × c̅) and is denoted by [a̅ b̅ c̅].

→ The magnitude |[a̅ b̅ c̅]| gives the volume of the parallelopiped with a̅, b̅, c̅ as its coterminus edges.

→ If a̅ = a₁i̅ + a₂ j̅ + a₃k̅, b̅ = b₁ i̅ + b₂ j̅ + b₃k̅, c̅ = c₁ i̅ + c₂ j̅ + c₃k̅ then
[a̅ b̅ c̅] = \(\left|\begin{array}{lll}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|\)

• Volume of the tetrahedron with a, b,c as its coterminus edges is V = \(\frac{1}{6}\)| [a̅ b̅ c̅]|
• Volume of tetrahedron ABCD is V = \(\frac{1}{6}|[\overline{\mathrm{AB}} \overline{\mathrm{AC}} \overline{\mathrm{AD}}]|\)

→ Three vectors a, b,c are coplanar ⇔ [a̅ b̅ c̅] = 0 and a, b,c are non – coplanar ⇔ [a̅ b̅ c̅] ≠ 0

→ The shortest distance between the skew lines r̅ = a̅ + tb̅ and r̅ = c̅ + sd̅ where s, t are scalars is \(\)

→ Vector triple product of three vectors a̅, b̅, c̅ is a vector defined by
(a̅ × b̅) × c̅ = (a̅. c̅)b̅ – (c̅ . b̅)a̅ (or) a̅ × (b̅ × c̅) = (a̅. c̅)b̅ – (a̅ . b̅)c̅

→ The vector equation of a plane passing through the point A(a̅) and parallel to two non – collinear vectors b̅ and c̅ is [r̅ b̅ c̅] = [a̅ b̅ c̅]

→ The vector equation of a plane passing through A(a̅), B(b̅) and parallel to the vector is [r̅ b̅ c̅] + [r̅ c̅ a̅] = [a̅ b̅ c̅]

→ The vector equation of a plane passing through three non colilnear points A(a̅), B(b̅) and C(c̅) is [r̅ b̅ c̅] + [r̅ c̅ a̅] + [r̅ a̅ b̅] = [a̅ b̅ c̅]

→ The vector equation of the plane containing the line r̅ = a̅ + tb̅; t ∈ R and perpendicular to the plane r̅.c̅ = q is [r̅ b̅ c̅] = [a̅ b̅ c̅]

• If a̅, b̅ are two non zero and non parallel vectors then |a̅ × b̅|² = a²b² – (a̅ . b̅) = \(\left|\begin{array}{cc}
  \bar{a} \cdot \bar{a} & \bar{a} \cdot \bar{b} \\
  \bar{a} \cdot \bar{b} & \bar{b} \cdot \bar{b}
  \end{array}\right|\)
• For any vector a̅, (a̅ × i̅) + (a̅ × j̅) + (a̅ × k̅) = 2|a̅|.
• If a̅, b̅, c̅ are the position vectors of the points A, B, C then the perpendicular distance from C to the line AB is = \(\frac{|\overline{\mathrm{AC}} \times \overline{\mathrm{AB}}|}{|\overline{\mathrm{AB}}|}=\frac{|(\overline{\mathrm{b}} \times \overline{\mathrm{c}})+(\overline{\mathrm{c}} \times \overline{\mathrm{a}})+(\overline{\mathrm{a}} \times \overline{\mathrm{b}})|}{|\overline{\mathrm{b}}-\overline{\mathrm{a}}|}\).