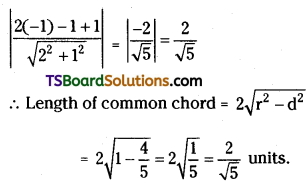Mahesh

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Quadratic Expressions Important Questions Very Short Answer Type

Question 1.
Find the roots of the quadratic equation ax² + bx + c = 0. [March ’02]
Solution:
Given quadratic equation is ax² + bx + c = 0
Now, multiplying with ‘4a’ on both sides
4a (ax² + bx – c) = 0
= 4ax²x² + 4abx + 4ac = 0
(2ax)² + 2 . 2ax . b + b² + b² – b² + 4ac = 0
(2ax + b)² = b² – 4ac
2ax + b = ± \(\sqrt{b^2-4 a c}\)
2ax = – b ± \(\sqrt{b^2-4 a c}\)
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ The roots of the quadratic equation, ax² + bx + c = 0 are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\).

Question 2.
Fmd the roots of the following equation √3x² + 10x – 8√3 = 0.
Solution:
Given quadratic equation is √3x² + 10x – 8√3 = 0
Comparing this with ax² + bx + c = 0,
we have a = √3, b = 10 c = – 8√3
The roots of quadratic equation are \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-10 \pm \sqrt{100+96}}{2 \sqrt{3}}=\frac{-10 \pm \sqrt{196}}{2 \sqrt{3}}\)
= \(\frac{-10 \pm 14}{2 \sqrt{3}}=\frac{-10+14}{2 \sqrt{3}} \text { (or) } \frac{-10-14}{2 \sqrt{3}}\)
= \(\frac{4}{2 \sqrt{3}} \text { (or) } \frac{-24}{2 \sqrt{3}}=\frac{2}{\sqrt{3}} \text { (or) } \frac{-12}{\sqrt{3}}\)
= \(\frac{2}{\sqrt{3}}\) (or) – 4√3
∴ The roots of the quadratic equation are \(\frac{2}{\sqrt{3}}\) (or) – 4√3

Question 3.
Form a quadratic equation whose roots are 7 ± 2√5. [TS – May ’16; March ’11, ’05, AP – March 2018]
Solution:
Let α = 7 + 2√5, β = 7 – 2√5
Now, α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – 20 = 29
The quadratic equation whose roots are α, β is
x² – (α + β)x + αβ = 0
x² – 14x + 29 = 0.

Question 4.
Form a quadratic equation whose roots are – 3 ± 5i.
Solution:
Let α = – 3 + 5i, β = – 3 – 5i
Now, α + β = – 3 + 5i – 3 – 5i = – 6
αβ = (- 3 + 5i) (- 3 – 5i)
= 9 – 25i² = 34
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
⇒ x² + 6x + 34 = 0

Question 5.
Form a quadratic equation whose roots are \(\frac{p-q}{p+q}\), – \(\frac{p+q}{p-q}\) (p ≠ q).
Solution:

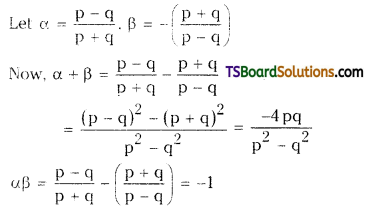
The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
x² + \(\frac{4 p q}{p^2-q^2}\) . x – 1 = 0
⇒ (p² – q²)x² + 4pqx – (p² – q²) = 0

Question 6.
Find the nature of the roots of 4x² – 20x + 25 = 0.
Solution:
Given quadratic equation is 4x² – 20x + 25 = 0.
Comparing this with ax² + bx + c = 0, we get
a = 4; b = – 20; c = 25
b² – 4ac = 400 – 4 . 4 . 25 = 400 – 400 = 0
Since ² – 4ac = 0 then the roots of the given equation are real and equal.

Question 7.
Find the nature of the roots of 2x² – 8x + 3 = 0.
Solution:
Given quadratic equation is 2x² – 8x + 3 = 0
Comparing this with ax² + bx + c = 0, we get
a = 2, b = – 8, c = 3
Now, b² – 4ac = 64 – 4 . 2 . 3
Since, b² – 4ac > 0 then the roots of the given equation are real and distinct.

Question 8.
Find the nature of the roots of 2x² – 7x + 10 = 0.
Solution:
Given quadratic equation is 2x² – 7x + 10 = 0
Comparing this with ax² + bx + c = 0, we get a = 2, b = – 7, c = 10
Now, b² – 4ac = 49 – 80 = – 31 < 0
Since, b² – 4ac < 0 then the roots of the given equation are conjugate complex numbers.

Question 9.
Find the nature of the roots of 3x² + 7x + 2 = 0.
Solution:
Given quadratic equation is 3x² + 7x + 2 = 0
Comparing this with ax² + bx + c = 0, we get a = 3, b = 7, c = 2
Now, b² – 4ac = 49 – 4 . 3 . 2
= 49 – 24 = 25 = 52 > 0
Since, b² – 4ac > 0 then the roots of the given equation are rational and unequal.

Question 10.
If α, β are the roots of ax² + bx + c = 0 then find \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}\).
Solution:
If α, β are the roots of ax² + bx + c = 0 then
α + β = \(\frac{-b}{a}\)
αβ = \(\frac{c}{a}\)
Now, \(\frac{1}{\alpha^2}+\frac{1}{\beta^2}=\frac{\beta^2+\alpha^2}{\alpha^2 \beta^2}=\frac{(\alpha+\beta)^2-2 \alpha \beta}{(\alpha \beta)^2}\)
= \(\frac{\left(\frac{-b}{a}\right)^2-2 \cdot \frac{c}{a}}{\left(\frac{c}{a}\right)^2}=\frac{b^2-2 c a}{c^2}\)

Question 11.
If α, β are the roots of ax² + bx + c = 0 then find \(\frac{1}{\alpha}+\frac{1}{\beta}\). [March ’10]
Solution:
If α, β are the roots of ax² + bx + c = 0
then α + β = \(\frac{-b}{a}\)
αβ = \(\frac{c}{a}\)
Now \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{\frac{-b}{a}}{\frac{c}{a}}=\frac{-b}{c}\)

Question 12.
If α, β are the roots of ax² + bx + c = 0 then find α² + β². [May ’13]
Solution:
If α, β are the roots of ax² + bx + c = 0
then α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)
Now α² + β² = (α + β)² – 2αβ
= \(\left(\frac{-b}{a}\right)^2-\frac{2 c}{a}=\frac{b^2}{a^2}-\frac{2 c}{a}=\frac{b^2-2 a c}{a^2}\).

Question 13.
For what values of m, the equation x² – 15 – m (2x – 8) = 0 will have equal roots ?
[March ’13 ’04, May ’08, TS – Mar. 2015; AP – Mar. ’19,’17]
Solution:
Given equation is x² – 15 – m (2x – 8) = 0
x² – 15 – 2mx + 8m = 0
⇒ x² – 2mx + 8m- 15 = 0 ……………(1)
Comparing this equation with
ax² + bx + c = 0, we get
a = 1, b = – 2m, c = 8m – 15
Since (1) have equal roots
⇒ b² – 4ac = 0
⇒ 4m² – 4 (1) (8m – 15) = 0
⇒ 4m² – 32m + 60 = 0
⇒ m² – 8m + 15 = 0
⇒ m² – 5m – 3m+ 15 = 0
⇒ m (m – 5) – 3 (m – 5) = 0
⇒ (m – 3) (m – 5) = 0
⇒ m = 3 (or) m = 5
∴ The values of m are 3, 5.

Question 14.
For what values of in, (m + 1) x² + 2(m + 3) x + (m + 8) = 0 has equal roots? [March ‘03]
Solution:
Given quadratic equation is (m + 1) x² + 2 (m + 3) x +(m + 8) = 0 …………..(1)
Comparing this with ax² + bx + c = 0, we get
a = m + 1, b = 2 (m + 3), c = m + 8
Since (1) have equal roots then b² – 4ac =0
⇒ [2 (m + 3)]² – 4 (m + 1) (m + 8) = 0
⇒ 4 (m + 3)² – 4(m + 1) (m + 8) = 0
⇒ m² + 6m + 9 – m² – 8m – m – 8 = 0
⇒ – 3m – 1 = 0 m = \(\frac{1}{3}\)

Question 15.
For what values of m, (3m + 1) x² + 2(m + 1) x + m = 0 will have equal roots?
Solution:
Given quadratic equation is (3m + 1)x² + 2(m + 1)x +m = 0 ………….(1)
Comparing this with ax² + bx + c = 0, we get
a = 3m + 1, b = 2(m + 1), c = m
since (1) have equal roots then b² – 4ac = 0
4 (m + 1)² – 4m (3m + 1) = 0
m² + 2m + 1 – 3m² – m = 0
– 2m² + m + 1 = 0
2m² – m – 1 = 0
2m² – 2m + m – 1 = 0
2m (m – 1) + 1 (m – 1) = 0
(m – 1) (2m + 1) = 0
m = 1, m = – \(\frac{1}{2}\)

Question 16.
Prove that the roots of (x – a) (x – b) = h² are always real. [AP – May 2013, May ’09]
Solution:
Given quadratic equation is
(x – a) (x – b) = h²
⇒ x² – ax – bx + ab – h² = 0
⇒ x² + (- a – b)x + ab – h² = 0
Comparing this with ax² + bx + c =0, we get
⇒ a = 1, b = – a – b, c = ab – h²
Now,
b² – 4ac = (- a – b)² – 4 (1) (ab – h²)
= a² + b² + 2ab – 4ab + 4h²
=(a² + b² – 2ab) + 4h²
= (a – b)² + (2h)² > 0
Since b² – 4ac > 0 then the roots of the given equation are always real.

Question 17.
Find the quadratic equation, the sum of whose roots is 1 and sum of the sqares of the roots is 13. [May ’07]
Solution:
Let α, β be the roots of required equation.
Given that, the sum of roots, α + β = 1
Sum of squares of the roots, α² + β² = 13
We know that, (α + β)² = α² + β² + 2αβ
⇒ 1 = 13 + 2αβ
⇒ 2αβ = – 12
⇒ αβ = – 6
∴ The quadratic equation whose roots are α, β is x² – (α + β)x + αβ = 0
⇒ x² – x – 6 = 0

Question 18.
Solve the equation 4^{x – 1} – 3 . 2^{x – 1} + 2 = 0. [March ’04]
Solution:
Given equation is 4^{x – 1} – 3 . 2^{x – 1} + 2 = 0
\(\frac{4^x}{4}-3 \cdot \frac{2^x}{2}+2\) = 0
\(\frac{\left(2^2\right)^x}{4}-3 \cdot \frac{2^x}{2}+2\) = 0
\(\frac{\left(2^x\right)^2}{4}-3 \cdot \frac{2^x}{2}+2\) = 0
Let 2^x = a
⇒ \(\frac{\mathrm{a}^2}{4}-\frac{3 \mathrm{a}}{2}\) + 2 = 0
⇒ a² – 6a + 8 = 0
⇒ a² – 4a – 2a + 8 = 0
⇒ (a – 4) (a – 2) = 0
⇒ a = 4 (or) 2.

Case – I:
lf a = 4
⇒ 2^x = 4
⇒ 2^x = 2²
⇒ x = 2.

Case – 2:
If a = 2
⇒ 2^x = 2
⇒ x = 1
∴ The solution set of the given equation is {2, 1}.

Question 19.
Find the maximum or minimum of the expression 12x – x² – 32 x varies over R.
Solution:
Given quadratic expression is – x + 12x – 32
Comparing this expression with ax + bx + c, we have a = – 1, b = 12, c = – 32
Here a = – 1 < 0.
Then – x² + 12x – 32 has absolute maximum at x = \(\frac{-b}{2 a}=\frac{-12}{2(-1)}\) = 6
∴ The maximum value = \(\frac{4 a c-b^2}{4 a}\)
= \(\frac{4(-1)(-32)-144}{4(-1)}\)
= \(\frac{128-144}{-4}=\frac{-16}{-4}\) = 4.

Question 20.
If the quadratic equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0, (b ≠ c) have a common root then show that a + 4b + 4c = 0.
Solution:
Given quadratic equations are ax² + 2bx + c = 0
Comparing this equation with a₁x² + b₁x + c₁ = 0, we get
a₁ = a, b₁ = 2b, c₁ = c
Now, a₂x + 2cx + b = 0
Comparing this with a₂x² + b₂x + c₂ = 0
we get a₂ = a, b₂ = 2c, c₂ = b
The condition for two quadratic equations
a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0 to have a common root is
(c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁)
⇒ (ca – ba)² = (a₂c – a₂b) (2bb – 2cc)
⇒ a² (c – b)² = 2a (c – b) 2 (b² – c²)
⇒ a² (c – b)² = 4a (c – b) (b – c) (c – b)
⇒ a = – 4 (c + b) a = – 4c – 4b
a + 4b + 4c = 0.

Question 21.
If x² – 6x + 5 = 0 and x² – 12x + p = 0 have a common root, then find p. [TS – May 2015, Mar. 2017]
Solution:
Given quadratic equations are x² – 6x + 5 = 0
Comparing this equation with
a₁x² + b₁x + c₁ = 0, we get
a₁ = 1, b₁ = – 6, c₁ = 5
Now, x² – 12x + p = 0,
Corn paring with a₂x² + b₂x + c₂ = 0
we get a₂ = 1, b₂ = – 12, c₂ = p
The condition for two quadratic equations
a₁x² + b₁x + c₁ = 0 and a₂x2 + b₂x + c₂ = 0 to have a common root is
(c₁a₂ – c₂a₁)² = (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁)
(5 (1) – p(1))² = (1 (- 12) – 1 (- 6)) ((- 6)p – (- 12) 5)
⇒ (5 – p)² = – 6 (- 6p + 60)
⇒ p² + 25 – 10p = 36p – 360
⇒ p² – 16p + 385 = 0
⇒ p² – 35p – 11p + 385 = 0
⇒ p (p – 35) – 11 (p – 35) = 0
⇒ (p – 11) (p – 35) = 0
⇒ p = 11 (or) p = 35
∴ p = 11 (or) 35.

Question 22.
For what values of x, the expression x² – 5x + 6 is positive?
Solution:
The given quadratic expression is x² – 5x + 6
⇒ x² – 3x – 2x + 6 = x (x – 3) – 2 (x – 3) = (x – 2)(x – 3)
i) If 2 < x < 3 then the expression x² – 5x + 6 is ‘- ve’.
ii) If x < 2 (or) x> 3 then the expression x² – 5x + 6 is ‘+ ve’.
iii) If x = 2 (or) x = 3 then the expression x² – 5x + 6 = 0

Question 23.
For what values of x, the expression x² – 5x – 6 is negative? [March ‘95]
Solution:
Given quadratic expression is x² – 5x – 6
= x² – 6x + x – 6
= x (x – 6) + 1 (x – 6)
= (x + 1)(x – 6)
i) If – 1 < x < 6 then the expression x² – 5x – 6 is ‘-ve’.
ii) If x < – 1 or x > 6 then the expression x² – 5x – 6 is ‘+ ve’.
iii) If x = – 1 (or) x = 6 then the expression x² – 5x – 6 = 0.

Question 24.
Discuss the signs of the expression x² – 5x + 4 for x ∈ R. [May ’95].
Solution:
Given quadratic expression is x² – 5x + 4
= x² – 4x – x + 4
= x (x – 4) + 1 (x – 4)
= (x – 1) (x – 4)
i) If 1 < x < 4 then the expression x² – 5x + 4 is ’-ve’.
ii) If x < 1 (or) x > 4 then the expression x² – 5x + 4 is ’+ve’.
iii) If x = 1 (or) x = 4 then the expression x² – 5x + 4 = 0.

Question 25.
Find the maximum or minimum value of the expression 12x – x² – 32. [May ’06]
Solution:
Given quadratic expression is – x² + 12x – 32 = 0
Comparing this expression with ax² + bx + c, we have a = – 1, b = 12, c = – 32
Here, a = – 1 < 0.
Then – x² + 12x – 32 has absolute maximum at x = \(\frac{-b}{2 a}=\frac{-12}{2(-1)}\) = 6
The maximum value = \(\frac{4 a c-b^2}{4 a}\)
= \(\frac{4(-1)(-32)-144}{4(-1)}=\frac{128-144}{-4}\)
= \(\frac{-16}{-4}\) = 4.

Question 26.
Find the maximum or minimum value of the expression 2x – 7 – 5x². [May ’10. March ’14, ’12].
Solution:
Given quadratic expression is – 5x² + 2x – 7
Comparing this expression with ax² + bx + c,
we have a = – 5, b = 2, c = – 7
Here, a = – 5 < 0, – 5x² + 2x – 7 has absolute maximum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(-5)}=\frac{1}{5}\)
∴ Maximum value is \(\frac{4 a c-b^2}{4 a}=\frac{4(-5)(-7)-4}{4(-5)}\)
= \(\frac{140-4}{-20}=\frac{136}{-20}=\frac{-34}{5}\)

Question 27.
Find the maximum or minimum value of the expression 3x² + 2x + 11. [May ’92]
Solution:
Given quadratic expression is 3x² + 2x + 11
Comparing this expression with ax² + bx + c, we have a = 3, b = 2, c = 11
Here, a = 3 >0, 3x² + 2x + 11 has absolute minimum at
x = \(\frac{-b}{2 a}=\frac{-2}{2(3)}=\frac{-1}{3}\)
∴ The minimum value = \(\frac{4 a c-b^2}{4 a}=\frac{4(3)(11)-4}{4(3)}\)
= \(\frac{132-4}{12}=\frac{128}{12}=\frac{32}{3}\).

Question 28.
Find the maximum or minimum value of the expression x² – x + 7 as x varies over R. [May ’14]
Solution:
Given quadratic expression is x² – x + 7
Comparing this expression with ax² + bx + c, we have a = 1, b = – 1, c = 7
Here, a = 1 > 0, x² – x + 7 has absolute minimum at x = \(\frac{-b}{2 a}=\frac{-(-1)}{2 \cdot 1}=\frac{1}{2}\)
∴ The minimum value = \(\frac{4 a c-b^2}{4 a}=\frac{4(1)(7)-(-1)^2}{4(1)}\)
= \(\frac{28-1}{4}=\frac{27}{4}\)

Question 29.
Find the roots of the equation 6√5 x² – 9x – 3√5 = 0.
Solution:
\(\frac{\sqrt{5}}{2}, \frac{-1}{\sqrt{5}}\)

Question 30.
Form a quadratic equation whose roots are 2√3 – 5 and – 2√3 – 5.
Solution:
x² + 10x + 13 = 0.

Question 31.
Form a quadratic equation whose roots are \(\frac{\mathbf{m}}{\mathbf{n}}, \frac{-\mathbf{n}}{\mathbf{m}}\), (m ≠ 0, n ≠ 0)
Solution:
mnx² – (m² – n²)x – mn = 0

Question 32.
If α, β are the roots of ax² + bx + c = 0 then find α³ + β³.
Solution:
\(\frac{3 a b c-b^3}{a^3}\)

Question 33.
For what values of m, x² + (m + 3) x + (m + 6) = 0 will have equal roots?
Solution:
m = 3, – 5.

Question 34.
For what values of m, z² – 2 (1 + 3m) x + 7 (3 + 2m) = 0 will have equal roots?
Solution:
m = 2, \(\frac{-10}{9}\).

Question 35.
For what vaIueof m, (2m+ 1)x² + 2(m + 3)x + (m + 5) = 0 will have equal rooti?
Solution:
m = \(\frac{-5 \pm \sqrt{41}}{2}\)

Question 36.
Find the quadratic equation, the sum of whose roots is 7 and sum of the squares of the roots is 25.
Solution:
x² – 7x + 12 = 0

Question 37.
So1ve the equation 3^{1 + x} + 3^{1 – x} = 10.
Solution:
{- 1, 1}

Question 38.
Solve 7^{1 + x} + 7^{1 – x} = 50 for real x.
Solution:
{- 1, 1}

Question 39.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
4 (or) 2.

Question 40.
For what values of x, the expression x² – 5x + 14 is positive?
Solution:
∀ x ∈ R

Question 41.
For what values of x, the expression 3x² + 4x + 4 is positive?
Solution:
∀ x ∈ R

Question 42.
For what values of x, the expression x² – 7x + 10 is negative?
Solution:
2 < x < 5

Question 43.
For what values of x, the expression 15 + 4x – 3x² is negative? [AP – Mar. 2015]
Solution:
x < – \(\frac{5}{3}\) (or) x > 3.

Question 44.
Find the changes in the sign of 4x – 5x² + 2 for x ∈ R.
Solution:
Positive for \(\frac{2-\sqrt{14}}{5}<x<\frac{2+\sqrt{14}}{5}\)
negative for x < \(\frac{2-\sqrt{14}}{5}\) (or) x > \(\frac{2+\sqrt{14}}{5}\)

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B System of Circles Important Questions Short Answer Type

Question 1.
Find the equation of the circle which passes through the origin and intersects the circles x² + y² – 4x – 6y – 3 = 0, x² + y² – 8y + 12 = 0 orthogonally.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …………(1)
Since (1) passes through the point (0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Given equations of the circles are
x² + y² – 4x – 6y – 3 = 0 ……..(2)
x² + y² – 8y + 12 = 0 ……….(3)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-3) = 0 – 3
⇒ -4g – 6f = -3
⇒ 4g + 6f – 3 = 0 …….(4)
Since (1) and (3) are orthogonal, then
2gg’ + 2ff’ = c + c’
⇒ 2g(0) + 2f(-4) = 0 + 12
⇒ -8f = 12
⇒ f = \(\frac{-3}{2}\)
Substituting the value of ‘f’ in (4)
4g + 6(\(\frac{-3}{2}\)) – 3 = 0
⇒ 4g – 9 – 3 = 0
⇒ 4g = 12
⇒ g = 3
∴ The equation of the required circle is
x² + y² + 2(3)x + 2(\(\frac{-3}{2}\))y + 0 = 0
x² + y² + 6x – 3y = 0

Question 2.
Find the equation of the circle which passes through the origin and intersects the circles x² + y² – 4x + 6y + 10 = 0, x² + y² + 12y + 6 = 0 orthogonally. [(AP) May ’18]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Since, (1) passes through the point (0, 0) then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
⇒ c = 0
Given equations of the circles are
x² + y² – 4x + 6y + 10 = 0 ……..(2)
x² + y² + 12y + 6 = 0 …….(3)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2(g)(-2) + 2f(3) = c + 10
⇒ -4g + 6f = 0 + 10
⇒ -4g + 6f = 10
⇒ 2g – 3f = -5
⇒ 2g – 3f + 5 = 0 ……..(4)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(0) + 2f(6) = 0 + 6
⇒ 12f = 6
⇒ f = \(\frac{1}{2}\)
Substituting the value of f in (4)
2g – 3(\(\frac{1}{2}\)) + 5 = 0
⇒ 2g + \(\frac{7}{2}\) = 0
⇒ g = \(\frac{-7}{4}\)
∴ The equation of the required circle is from (1)
x² + y² + 2(\(\frac{-7}{4}\))x + 2(\(\frac{1}{2}\))y + 0 = 0
⇒ x² + y² – \(\frac{7}{2}\)x + y = 0
⇒ 2x² + 2y² – 7x + 2y = 0

Question 3.
Find the equation of the circle which passes through (1, 1) and cuts orthogonally each of the circles x² + y² – 8x – 2y + 16 = 0 and x² + y² – 4x – 4y – 1 = 0.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through point (1, 1) then
(1)² + (1)² – 2g(1) – 2f(1) + c = 0
⇒ 2 + 2g + 2f + c = 0
⇒ 2g + 2f + c = -2 …….(2)
Given equations of the circles are
x² + y² – 8x – 2y + 16 = 0 ……..(3)
x² + y² – 4x – 4y – 1 = 0 ………(4)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-4) + 2f(-1) = c + 16
⇒ -8g – 2f – c = 16 ………(5)
Since (1) and (4) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-2) = c – 1
⇒ -4g – 4f – c = -1
From (2) and (5)
2g + 2f + c = -2
⇒ -8g – 2f – c = 16
⇒ -6g = 14
⇒ g = \(\frac{-7}{3}\)
From (5) and (6)

Substituting the values of g, f in (2)

∴ The equation of the required circle is from (1),
x² + y² + 2(\(\frac{-7}{3}\))x + 2(\(\frac{23}{6}\))y – 5 = 0
⇒ 3x² + 3y² – 14x + 23y – 15 = 0

Question 4.
Find the equation of the circle which passes through the point (0, -3) and intersects the circles given by the equations x² + y² – 6x + 3y + 5 = 0 and x² + y² – x – 7y = 0 orthogonally. [May ’15 (TS) May ’13]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since eq (1) passes through the point (0, -3) then
9 + 2f(-3) + c = 0
⇒ 9 – 6f + c = 0
⇒ -6f + c = -9 ……..(2)
Given equations of the circles are
x² + y² – 6x + 3y + 5 = 0 ………(3)
x² + y² – x – 7y = 0 ………(4)
Since the circles (1) & (3) are orthogonal then 2gg’ + 2ff’ = c + c’
⇒ 2g(-3) + 2f(\(\frac{3}{2}\)) = c + 5
⇒ -6g + 3f – c = 5 …….(5)
Since the circles (1) & (4) are orthogonal then 2gg’ + 2ff’ = c + c’

Question 5.
Find the equation of the circle passing through the origin having its centre on the line x + y = 4 and intersecting the circle x² + y² – 4x + 2y + 4 = 0 orthogonally.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since eq. (1) passes through the point (0, 0) then c = 0
Centre of (1), C = (-g, -f) lies on the line
x + y = 4 then -g – f = 4 ……..(2)
Given the equation of the circle is
x² + y² – 4x + 2y + 4 = 0 ……….(3)
Since the circles (1) & (3) are orthogonal then 2gg’ + 2ff’ = c + c’
2g(-2) + 2f(1) = c + 4
⇒ -4g + 2f = 4
⇒ -2g + f = 2 ……….(4)
Solve (2) & (4)


∴ The equation of the required circle is x² + y² + 2(-2)x + 2(-2)y + 0 = 0
⇒ x² + y² – 4x – 4y = 0

Question 6.
Find the equation of the circle passing through the points (2, 0), (0, 2) and orthogonal to the circle 2x² + 2y² + 5x – 6y + 4 = 0. [(TS) May ’19]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since, (1) passes through the point (2, 0), then
(2)² + (0)² + 2g(2) + 2f(0) + c = 0
⇒ 4 + 4g + c = 0
⇒ 4g + c = -4 ………(2)
Since (1) passes through the point (0, 2), then
(0)² + (2)² + 2g(0) + 2f(0) + c = 0
⇒ 4 + 4f + c = 0
⇒ 4f + c = -4 …….(3)
Given the equation of the circle is
2x² + 2y² + 5x – 6y + 4 = 0
⇒ x² + y² + \(\frac{5}{2}\)x – 3y + 2 = 0 ………(4)
Since (1) and (4) are orthogonal, then 2gg’ + 2ff’ = c + c’
2g(\(\frac{5}{4}\)) + 2f(\(\frac{-3}{2}\)) = c + 2
⇒ \(\frac{5g}{2}\) – 3f = c + 2
⇒ 5g – 6f = 2c + 4
⇒ 5g – 6f – 2c = 4 ………(5)

Question 7.
Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having the centre at (2, 3). [Mar. ’19 (TS)]
Solution:
Given the equation of the circle is
x² + y² – 4x + 2y – 7 = 0 ……….(1)
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(2)
centre (-g, -f) = (2, 3)
∴ g = -2, f = -3
since (1) &(2) are orthogonal then 2gg’ + 2ff’ = c + c’
⇒ 2(-2)(-2) + 2(-3)(1) = -7 + c
⇒ 8 – 6 = -7 + c
⇒ 2 = -7 + c
⇒ c = 7 + 2
⇒ c = 9
∴ The equation of the required circle is x² + y² – 4x – 6y + 9 = 0

Question 8.
Find the equation of the circle which is orthogonal to each of the following three circles x² + y² + 2x + 17y + 4 = 0, x² + y² + 7x + 6y + 11 = 0, and x² + y² – x + 22y + 3 = 0. [May ’08; Mar. ’03]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……..(1)
Given equations of the circles are
x² + y² + 2x + 17y + 4 = 0 ……..(2)
x² + y² + 7x + 6y + 11 = 0 ……..(3)
x² + y² – x + 22y + 3 = 0 ……….(4)
Since the circles (1) & (2) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(1) + 2f(\(\frac{17}{2}\)) = c + 4
⇒ 2g + 17f = c + 4 ……….(5)
Since the circles (1) & (3) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(\(\frac{7}{2}\)) + 2f(3) = c + 11
⇒ 7g + 6f – c = 11 ………(6)
Since the circles (1) & (4) are orthogonal to each other then
2gg’ + 2ff’ = c + c’
⇒ 2g(\(\frac{-1}{2}\)) + 2f(11) = c + 3
⇒ -g + 22f – c = 3 ………(7)
From (5) & (6)

Substitute g, f values in eq. (5)
2(-3) + 17(-2) – c = 4
⇒ -6 – 34 – c = 4
⇒ c = -44
∴ The equation of the required circle is x² + y² + 2(-3)x + 2(-2)y – 44 = 0
⇒ x² + y² – 6x – 4y – 44 = 0

Question 9.
Find the equation of the circle which cuts the circles x² + y² + 2x + 4y + 1 = 0, 2x² + 2y² + 6x + 8y – 3 = 0, x² + y² – 2x + 6y – 3 = 0 orthogonally.
Solution:
Given equations of the circles are
S = x² + y² + 2x + 4y + 1 = 0
S’ = 2x² + 2y² + 6x + 8y – 3 = 0
S’ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
S” = x² + y² – 2x + 6y – 3 = 0
The equation of the radical axis of the circles S = 0 and S’ = 0 are S – S’ = 0
⇒ x² + y² + 2x + 4y + 1 – (x² + y² + 3x + 4y – \(\frac{3}{2}\)) = 0
⇒ x² + y² + 2x + 4y + 1 – x² – y² – 3x – 4y + \(\frac{3}{2}\) = 0
⇒ -x + 1 + \(\frac{3}{2}\) = 0
⇒ -2x + 2 + 3 = 0
⇒ 2x – 5 = 0 ……..(1)
The equation of the radical axis of the circles S’ = 0 and S” = 0 is S’ – S” = 0
⇒ x² + y² + 3x + 4y – \(\frac{3}{2}\) – (x² + y² – 2x + 6y – 3) = 0
⇒ x² + y² + 3x + 4y – \(\frac{3}{2}\) – x² – y² + 2x – 6y + 3 = 0
⇒ 5x – 2y – \(\frac{3}{2}\) + 3 = 0
⇒ 10x – 4y – 3 + 6 = 0
⇒ 10x – 4y + 3 = 0 ……..(2)
Solving (1) and (2)

∴ Radical centre, C = (\(\frac{5}{2}\), 7) = centre of the required circle.
Radius of the required circle, r = the length of tangent from the radical centre, C = (\(\frac{5}{2}\), 7) of the circle is \(\sqrt{\mathrm{S}_{11}}\)

4x² + 25 – 20x + 4y² – 56y + 196 = 357
x² + y² – 5x – 14y – 34 = 0

Question 10.
Find the equation of the circle which intersects each of the following circles orthogonally.
x² + y² + 4x + 2y + 1 = 0, 2(x² + y²) + 8x + 6y – 3 = 0, x² + y² + 6x – 2y – 3 = 0
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ……(1)
Given equations of the circles are
x² + y² + 4x + 2y + 1 = 0 …….(2)
2(x² + y²) + 8x + 6y – 3 = 0
x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ………(3)
x² + y² + 6x – 2y – 3 = 0 ……..(4)
Since (1) and (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(2) + 2f(1) = c + 1
⇒ 4g + 2f = c + 1
⇒ 4g + 2f – c = 1 ………(5)
Since (1) and (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(2) + 2f(\(\frac{3}{2}\)) = c – \(\frac{3}{2}\)
⇒ 4g + 3f = c – \(\frac{3}{2}\)
⇒ 4g + 3f – c = \(-\frac{3}{2}\) ………(6)
Since (1) and (4) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(3) + 2f(-1) = c – 3
⇒ 6g- 2f = c – 3
⇒ 6g – 2f – c = -3 ………(7)
From (5) and (6)


∴ The equation of the required circle is from (1)
x² + y² + 2(-7)x + 2(\(\frac{-5}{2}\))y – 34 = 0
⇒ x² + y² – 14x – 5y – 34 = 0

Question 11.
Find the equation of the circle which cuts the circles x² + y² – 4x – 6y + 11 = 0 and x² + y² – 10x – 4y + 21 = 0 orthogonally and has the diameter along the straight line 2x + 3y = 7. [Mar. ’16 (AP); May ’07]
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Given equations of the circles are
x² + y² – 4x – 6y + 11 = 0 ……..(2)
x² + y² – 10x – 4y + 21 = 0 ……..(3)
Since the circles (1) & (2) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-2) + 2f(-3) = c + 11
⇒ -4g – 6f – c = 11 ……..(4)
Since the circles (1) & (3) are orthogonal then
2gg’ + 2ff’ = c + c’
⇒ 2g(-5) + 2f(-2) = c + 21
⇒ -10g – 4f – c = 21 ……..(5)
Centre of (1) is C = (-g, -f) lies on the line 2x + 3y = 7 then
2(-g) + 3(-f) = 7
⇒ -2g – 3f = 7 ……..(6)
From (4) & (5)

Substitute the values of g, f in eq. (4)
-4(-2) – 6(-1) – c = 11
⇒ 8 + 6 – c = 11
⇒ 14 – c = 11
⇒ c = 3
∴ The equation of the required circle is x² + y² + 2(-2)x + 2(-1)y + 3 = 0
⇒ x² + y² – 4x – 2y + 3 = 0

Question 12.
Find the equation of the circle passing through the points of intersection of the circles x² + y² – 8x – 6y + 21 = 0, x² + y² – 2x – 15 = 0, and (1, 2). [Mar. ’19 (AP); (TS) May ’17]
Solution:

Given equations of the circles are
S = x² + y² – 8x – 6y + 21 = 0
S’ = x² + y² – 2x – 15 = 0
Let, the given point A = (1, 2)
The equation of the circle passing through A, B is S + λS’ = 0
(x² + y² – 8x – 6y + 21) + λ(x² + y² – 2x – 15) = 0 ……….(1)
Since, (1) passes through the point (1, 2) then
((1)² + (2)² – 8(1) – 6(2) + 21) + λ[(1)² + (2)² – 2(1) – 15] = 0
⇒ 1 + 4 – 8 – 12 + 21 + λ(1 + 4 – 2 – 15) = 0
⇒ 6 + λ(-12) = 0
⇒ -12λ = -6
⇒ λ = \(\frac{1}{2}\)
∴ The equation of the required circle is
From (1)
⇒ x² + y² – 8x – 6y + 21 + \(\frac{1}{2}\)(x² + y² – 2x – 15) = 0
⇒ 2x² + 2y² – 16x – 12y + 42 + x² + y² – 2x – 15 = 0
⇒ 3x² + 3y² – 18x – 12y + 27 = 0
⇒ x² + y² – 6x – 4y + 9 = 0

Question 13.
Find the equation of the circle passing through the intersection of the circles x² + y² = 2ax and x² + y² = 2by and having its centre on the line \(\frac{x}{a}-\frac{\mathbf{y}}{b}\) = 2.
Solution:
Given equations of the circles are
S = x² + y² – 2ax = 0
S’ = x² + y² – 2by = 0

Given the equation of the straight line is
L = \(\frac{x}{a}-\frac{\mathbf{y}}{b}\) – 2 = 0
The equation of the circle passing through A, B is S + λS’ = 0
(x² + y² – 2ax) + λ(x² + y² – 2by) = 0 ……(1)
x² + y² – 2ax + λx² + λy² – 2λby = 0
(1 + λ) x² + (1 + λ) y² – 2ax – 2λby = 0

∴ The equation of the circle on \(\overline{\mathrm{AB}}\) as a diameter is from (1),
(x² + y² – 2ax) – \(\frac{1}{3}\) (x² + y² – 2by) = 0
⇒ 3x² + 3y² – 6ax – x² – y² + 2by = 0
⇒ 2x² + 2y² – 6ax + 2by = 0
⇒ x² + y² – 3ax + by = 0

Question 14.
If the straight line 2x + 3y = 1 intersects the circle x² + y² = 4 at points A and B then find the equation of the circle having \(\overline{\mathrm{AB}}\) as a diameter.
Solution:

Given equation of the circle is S = x² + y² – 4 = 0
Given the equation of the straight line is 2x + 3y – 1 = 0
The equation of the circle passing through A, B is S + λL = 0
x² + y² – 4 + λ(2x + 3y – 1) = 0 ………(1)
x² + y² – 4 + 2λx + 3λy – λ = 0
Here g = λ, f = \(\frac{3 \lambda}{2}\), c = -λ
Centre of the circle (1) is
C = (-g, -f) = (-λ, \(-\frac{3 \lambda}{2}\))
If \(\overline{\mathrm{AB}}\) is a diameter of a circle (1) then ‘C’ lies on 2x + 3y – 1 = 0
⇒ 2(-λ) + 3(\(-\frac{3 \lambda}{2}\)) – 1 = 0
⇒ -4λ – 9λ – 2 = 0
⇒ -13λ – 2 = 0
⇒ -13λ = 2
⇒ λ = \(\frac{-2}{13}\)
∴ The equation of the circle on \(\overline{\mathrm{AB}}\) as a diameter is, from (1)
⇒ x² + y² – \(\frac{2}{13}\) (2x + 3y – 1) = 0
⇒ 13x² + 13y² – 52 – 4x – 6y + 2 = 0
⇒ 13x² + 13y² – 4x – 6y – 50 = 0

Question 15.
If x + y = 3 is the equation of the chord AB of the circle x² + y² – 2x + 4y – 8 = 0. Find the equation of the circle having AB as the diameter. [(AP) May ’17, ’16, Mar. ’15]
Solution:
Given the equation of the circle is
S = x² + y² – 2x + 4y – 8 = 0

Given the equation of the straight line is
L = x + y – 3 = 0
The equation of the circle passing through A, B is S + λL = 0
(x² + y² – 2x + 4y – 8) + λ(x + y – 3) = 0 ……….(1)
x² + y² – 2x + 4y – 8 + λx + λy – 3λ = 0
x² + y² + (-2 + λ)x + (4 + λ)y – 8 – 3λ = 0
Here g = \(\frac{-2+\lambda}{2}\), f = \(\frac{4+\lambda}{2}\), c = -8 – 3λ
Centre of the circle (1) is
c = (-g, -f) = \(\left(\frac{2-\lambda}{2}, \frac{-4-\lambda}{2}\right)\)
If \(\overline{\mathrm{AB}}\) is diameter of circle (1), then ‘c’ lies on x + y – 3 = 0
⇒ \(\frac{2-\lambda}{2}+\frac{-4-\lambda}{2}-3=0\)
⇒ \(\frac{2-\lambda-4-\lambda-6}{2}=0\)
⇒ -8 – 2λ = 0
⇒ 2λ = -8
⇒ λ = -4
∴ The equation of the circle on \(\overline{\mathrm{AB}}\) as a diameter is from (1),
x² + y² – 2x + 4y – 8 – 4(x + y – 3) = 0
⇒ x² + y² – 2x + 4y – 8 – 4x – 4y + 12 = 0
⇒ x² + y² – 6x + 4 = 0

Question 16.
Find the radical centre of the three circles x² + y² – 4x – 6y + 5 = 0, x² + y² – 2x – 4y – 1 = 0, x² + y² – 6x – 2y = 0. [(AP) May ’19, Mar. ’18; (TS) May ’18]
Solution:
Given circles are
x² + y² – 4x – 6y + 5 = 0 …….(1)
x² + y² – 2x – 4y – 1 = 0 ……….(2)
x² + y² – 6x – 2y = 0 ……….(3)
The radical axis of (1) & (2) is
x² + y² – 4x – 6y + 5 – (x² + y² – 2x – 4y – 1) = 0
⇒ -2x – 2y + 6 = 0
⇒ x + y – 3 = 0 ……..(4)
The radical axis of (2) & (3) is
x² + y² – 2x – 4y – 1 – (x² + y² – 6x – 2y) = 0
⇒ 4x – 2y – 1 = 0 ……….(5)
Solving (4) & (5) we get

Question 17.
Find the radical centre of the circles x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y² + y = 0. [May ’16 (TS) May ’14]
Solution:
Given equations of the circles are
S = x² + y² + 4x – 7 = 0
S’ = 2x² + 2y² + 3x + 5y – 9 = 0
S’ = \(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}=0\)
S” = x² + y² + y = 0
The equation of the radical axis of the circles S = 0 and S’ = 0 is S – S’ = 0
⇒ (x² + y² + 4x – 7) – (\(x^2+y^2+\frac{3}{2} x+\frac{5}{2} y-\frac{9}{2}\)) = 0
⇒ x² + y² + 4x – 7 – x² – y² – \(\frac{3}{2} x-\frac{5}{2} y+\frac{9}{2}\) = 0
⇒ \(4 x-\frac{3}{2} x-7-\frac{5}{2} y+\frac{9}{2}=0\)
⇒ 8x – 3x – 14 – 5y + 9 = 0
⇒ 5x – 5y – 5 = 0
⇒ x – y – 1 = 0 ……..(1)
The equation of the radical axis of the circles S = 0 and S” = 0 is S – S” = 0
⇒ x² + y² + 4x – 7 – (x² + y² + y) = 0
⇒ x² + y² + 4x – 7 – x² – y² – y = 0
⇒ 4x – y – 7 = 0 ……….(2)
Solving (1) and (2)

∴ Radical centre = (2, 1)

Question 18.
Find the equation and length of the common chord of the two circles x² + y² + 3x + 5y + 4 = 0 and x² + y² + 5x + 3y + 4 = 0. [Mar. ’18 (TS)]

Solution:
Given circles are
x² + y² + 3x + 5y + 4 = 0 ………(1)
x² + y² + 5x + 3y + 4 = 0 ……….(2)
Equation of common chord of (1) & (2) as
x² + y² + 3x + 5y + 4 – (x² + y² + 5x + 3y + 4) = 0
⇒ -2x + 2y = 0
⇒ x – y = 0
The centre of 1st circle is c\(\left(\frac{-3}{2}, \frac{-5}{2}\right)\) and

Question 19.
Find the equation and length of the common chord of the circles x² + y² + 2x + 2y + 1 = 0, x² + y² + 4x + 3y + 2 = 0. [Mar. ’17 (AP & TS); May ’15 (AP)]
Solution:
Given circles are x² + y² + 2x + 2y + 1 = 0 …….(1)
and x² + y² + 4x + 3y + 2 = 0 ……..(2)
The common chord of (1) & (2) is
x² + y² + 2x + 2y + 1 – [x² + y² + 4x + 3y + 2] = 0
⇒ -2x – y – 1 = 0
⇒ 2x + y + 1 = 0
For the 1st circle x² + y² + 2x + 2y + 1 = 0
centre C = (-1, -1) and
radius r = \(\sqrt{1+1-1}\) = 1
d = perpendicular distance from (-1, -1) to the chord 2x + y + 1 = 0

Question 20.
Find the equation of the circle whose diameter is the common chord of the circles S = x² + y² + 2x + 3y + 1 = 0 and S’ = x² + y² + 4x + 3y + 2 = 0. (Apr. ’91)
Solution:
Given equations of the circles are,
S = x² + y² + 2x + 3y + 1 = 0
S’ = x² + y² + 4x + 3y + 2 = 0

The equation of the common chord of the circles S = 0 and S’ = 0 is S – S’ = 0
x² + y² + 2x + 3y + 1 – x² – y² – 4x – 3y – 2 = 0
2x + 1 = 0
L = 2x + 1 = 0
The equation of any circle passing through the point of intersection of S = 0 and L = 0 is S + λL = 0
(x² + y² + 2x + 3y + 1) + λ(2x + 1) = 0 ……..(1)
x² + y² + 2x + 3y + 1 + 2λx + λ = 0
x² + y² + 2(1 + λ)x + 3y + 1 + λ = 0
g = (1 + λ), f = \(\frac{3}{2}\)
Centre C = (-g, -f) = \(\left(-(1+\lambda), \frac{-3}{2}\right)\)
Since \(\overline{\mathrm{AB}}\) is a diameter of circle (1) then centre C(-1 – λ, \(\frac{-3}{2}\)) lies on the L = 0
2(-1 – λ) + 1 = 0
⇒ -2 – 2λ + 1 = 0
⇒ 2λ = -1
⇒ λ = \(\frac{-1}{2}\)
∴ The equation of the required circle is, from (1)
x² + y² + 2x + 3y + 1 – \(\frac{1}{2}\)(2x + 1) = 0
⇒ 2x² + 2y² + 4x + 6y + 2 – 2x – 1 = 0
⇒ 2x² + 2y² + 2x + 6y + 1 = 0

Question 21.
Show that the common chord of the circles x² + y² – 6x – 4y + 9 = 0, x² + y² – 8x – 6y + 23 = 0 is the diameter of the second circle, and also find its length.
Solution:
Given equations of the circles are
S = x² + y² – 6x – 4y + 9 = 0 ………(1)
S’ = x² + y² – 8x – 6y + 23 = 0 ………..(2)

The equation of the common chord of the circles S = 0 and S’ = 0 is S – S’ = 0
⇒ (x² + y² – 6x – 4y + 9) – (x² + y² – 8x – 6y + 23) = 0
⇒ x² + y² – 6x – 4y + 9 – x² – y² + 8x + 6y – 23 = 0
⇒ 2x + 2y – 14 = 0
⇒ x + y – 7 = 0 ……….(1)
Centre of the circle S’ = 0 is c = (-g, -f) = (4, 3)
The radius of the circle S’ = 0 is
r = \(\sqrt{(-4)^2+(-3)^2-23}\)
= \(\sqrt{16+9-23}\)
= √2
Now substituting the centre of the circle S’ = 0, c = (4, 3) in (1)
4 + 3 – 7 = 0
⇒ 7 – 7 = 0
⇒ 0 = 0
∴ (1) is the diameter of the second circle S’ = 0
Now, the length of the common chord = diameter of the second circle
= 2 × radius of the second circle
= 2r
= 2√2

Question 22.
Show that the circles x² + y² – 2x – 4y – 20 = 0 and x² + y² + 6x + 2y – 90 = 0 touch each other internally. Find the point of contact and the equation of common tangent. [(TS) Mar. ’15)]
Solution:
Given equations of the circles are
S = x² + y² – 2x – 4y – 20 = 0 …….(1)
S’ = x² + y² + 6x + 2y – 90 = 0 …….(2)
for the circle (1)
Centre C₁ = (1, 2)

|r₁ – r₂| = |5 – 10| = |-5| = 5
∴ c₁c₂ = |r₁ – r₂|
∴ Given circles touch each other internally.
Let ‘P’ be the point of contact.

Now ‘P’ divides C₁C₂ in the ratio r₁ : r₂ (5 : 10 = 1 : 2) externally.
∴ Point of contact

In this case, the common tangent is nothing but the radical axis.
∴ The equation of the common tangent (radical axis) of the circles S = 0 and S’ = 0 is S – S’ = 0
(x² + y² – 2x – 4y – 20) – (x² + y² + 6x + 2y – 90) = 0
⇒ x² + y² – 2x – 4y – 20 – x² – y² – 6x – 2y + 90 = 0
⇒ -8x – 6y + 70 = 0
⇒ 4x + 3y – 35 = 0

Question 23.
Show that the circles x² + y² – 8x – 2y + 8 = 0 and x² + y² – 2x + 6y + 6 = 0 touch each other and find the point of contact. (Mar. ’14)

Solution:
Given equations of the circles are
S = x² + y² – 8x – 2y + 8 = 0 ………(1)
S’ = x² + y² – 2x + 6y + 6 = 0 ……..(2)
For circle (1),
centre C₁ = (-g, -f) = (4, 1)


r₁ + r₂ = 3 + 2 = 5
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch other externally.
The point of contact, P divides C₁C₂ internally in the ratio (r₁ : r₂ = 3 : 2)

Question 24.
Show that the circles x² + y² – 2x = 0 and x² + y² + 6x – 6y + 2 = 0 touch each other. Find the coordinates of the point of contact. Is the point of contact external or internal?
Solution:

Given equations of the circles are
x² + y² – 2x = 0 ………(1)
x² + y² + 6x – 6y + 2 = 0 ……….(2)
For circle (1), centre, C₁ = (1, 0)


r₁ + r₂ = 1 + 4 = 5
∴ C₁C₂ = r₁ + r₂
∴ Given circles touch each other externally.
Let ‘P’ be the point of contact.
Now, the point of contact, ‘P’ divides C₁C₂ in the ratio r₁ : r₂ (1 : 4) internally.

∴ The point of contact is internal.

Question 25.
Show that the circles x² + y² + 2ax + c = 0 and x² + y² + 2by + c = 0 touch each other if \(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c}\).
Solution:
Given equations of the circles are
x² + y² + 2ax + c = 0 ………(1)
x² + y² + 2by + c = 0 ………(2)
Centre of (1) is C₁ = (-a, 0)
Radius of (1) is r₁ = \(\sqrt{a^2-c}\)
Centre of (2) is C₂ = (0, -b)
Radius of (2) is r₂ = \(\sqrt{b^2-c}\)
C₁C₂ = \(\sqrt{(-a+0)^2+(0+b)^2}=\sqrt{a^2+b^2}\)
Since the given two circles touch each other then
C₁C₂ = |r1 ± r2|
\(\sqrt{a^2+b^2}=\left|\sqrt{a^2-c} \pm \sqrt{b^2-c}\right|\)
Squaring on both sides

Question 26.
If the straight line represented by x cos α + y sin α = p intersects the circle x² + y² = a² at the points A and B then show that the equation of the circle with \(\overline{\mathbf{A B}}\) as the diameter is x² + y² – a² – 2p(x cos α + y sin α – p) = 0.
Solution:

Given the equation of the circle is
S = x² + y² – a² = 0
Given the equation of the straight line is
L = x cos α + y sin α – p = 0
The equation of the circle passing through A, B is S + λL = 0
(x² + y² – a²) + λ(x cos α + y sin α – p) = 0 ……(1)
x² + y² – a² + λx cos α + λy sin α – λp = 0
x² + y² + λ cos αx + λ sin αy – a² – λp = 0
Here,

The equation of the circle on \(\overline{\mathbf{A B}}\) as diameter is from (1)
(x² + y² – a²) – 2p(x cos α + y sin α – p) = 0

Question 27.
If the two circles x² + y² + 2gx + 2fy = 0 and x² + y² + 2g’x + 2f’y = 0 touch each other, then show that f’g = fg’. [(AP) Mar. ’20, (TS) ’16]
Solution:
Given equations of the circles are
x² + y² + 2gx + 2fy = 0 ……….(1)
x² + y² + 2g’x + 2f’y = 0 ……..(2)
For circle (1),
Center, C₁ = (-g, -f)
Radius, r₁ = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2}\)
For circle (2),
Center, C₂ = (-g’, -f’)
radius, r₂ = \(\sqrt{g^{\prime 2}+f^{\prime 2}}\)
Now, C₁C₂ = \(\sqrt{\left(-\mathrm{g}+\mathrm{g}^{\prime}\right)^2+\left(-\mathrm{f}+\mathrm{f}^{\prime}\right)^2}\)
Since the given circles touch each other then

Question 28.
Find the equation of a circle that cuts each of the following circles orthogonally. (Mar. ’07)
S’ = x² + y² + 3x + 2y + 1 = 0,
S” = x² + y² – x + 6y + 5 = 0,
S'” = x² + y² + 5x – 8y + 15 = 0
Solution:
Given equations of the circles are
S’ = x² + y² + 3x + 2y + 1 = 0
S” = x² + y² – x + 6y + 5 = 0
S'” = x² + y² + 5x – 8y + 15 = 0
The equation of the radical axis of S’ = 0 and S” = 0 is S’ – S” = 0
⇒ x² + y² + 3x + 2y + 1 – x² – y² + x – 6y – 5 = 0
⇒ 4x – 4y – 4 = 0
⇒ x – y – 1 = 0 ……….(1)
The equation of the radical axis of S” = 0 and S'” = 0 is S” – S'” = 0
⇒ x² + y² – x + 6y + 5 – x² – y² – 5x + 8y – 15 = 0
⇒ -6x + 14y – 10 = 0
⇒ -3x + 7y – 5 = 0
⇒ 3x – 7y + 5 = 0 ……….(2)
Solving (1) & (2)

∴ Radical centre = (3, 2) centre of the required circle
Radius = The length of the tangent from (3, 2) to the circle (1) is \(\sqrt{\mathrm{S}_{11}}\)

The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 3)² + (y – 2)² = 27
⇒ x² + 9 – 6x + y² + 4 – 4y – 27 = 0
⇒ x² + y² – 6x – 4y – 14 = 0

Question 29.
Prove that the radical axis of any two circles is perpendicular to the line joining their centres.
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0
S’ = x² + y² + 2g’x + 2f’y + c’ = 0 be the given circles.

The equation of the radical axis is S – S’ = 0
(x² + y² + 2gx + 2fy + c) – (x² + y² + 2g’x + 2f’y + c’) = 0
⇒ x² + y² + 2gx + 2fy + c – x² – y² – 2g’x – 2f’y – c’ = 0
⇒ 2(g – g’)x + 2(f – f’)y + c – c’ = 0
The slope of the radical axis is

∴ The radical axis is perpendicular to the line of centres.

Question 30.
Prove that the radical axis of the circle x² + y² + 2gx + 2fy + c = 0 and x² + y² + 2g’x + 2f’y + c’ = 0 is the diameter of the latter circle (or the former bisects the circumference of the latter) if 2g'(g – g’) + 2f'(f – f’) = c – c’.
Solution:
Given equations of the circles are
S = x² + y² + 2gx + 2fy + c = 0
S’ = x² + y² + 2g’x + 2f’y + c = 0

The equation of the radical axis of the circles S = 0 and S’ = 0 is S – S’ = 0
(x² + y² + 2gx – 2fy + c) – (x² + y² + 2g’x + 2f’y + c’) = 0
⇒ x² + y² + 2gx – 2fy + c – x² – y² – 2g’x – 2f’y – c’ = 0
⇒ 2(g – g’)x+2(f – f’)y + c – c’ = 0 ……(1)
Centre of the second circle S’ = 0 is c = (-g’, -f’)
Since (1) is the diameter of the second circle S’ = 0, then
substitute the centre of the second circle S’ = 0 is c = (-g’, -f’) in (1)
⇒ 2(g – g’)(-g’) + 2(f – f’)(-f’) + c – c’ = 0
⇒ 2g'(g – g’) + 2f(f – f’) = c – c’

Question 31.
If P and Q are conjugate with respect to a circle S = x² + y² + 2gx + 2fy + c = 0, then prove that the circle on PQ as diameter cuts the circle S = 0 orthogonally.
Solution:
Let P = (x₁, y₁) and Q = (x₂, y₂),
S = x² + y² + 2gx + 2fy + c = 0 ……….(1)
Given that, the two points P, Q are conjugate w.r.t a circle S = 0, then S₁₂ = 0
⇒ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0 ………(2)
The equation of the circle having \(\overline{\mathrm{PQ}}\) as diameter is
S’ = (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ x² – x₁x₂ – xx₁ + x₁x₂ + y² – yy₂ – yy₁ + y₁y₂ = 0
⇒ x² + y² – x(x₁ + x₂) – y(y₁ + y₂) + x₁x₂ + y₁y₂ = 0 ………(3)
Now, applying orthogonally condition S = 0 and S’ = 0
2gg’ + 2ff’ = \(2 \mathrm{~g}\left(\frac{-\left(\mathrm{x}_1+\mathrm{x}_2\right)}{2}\right)+2 \mathrm{f}\left(\frac{-\left(\mathrm{y}_1+\mathrm{y}_2\right)}{2}\right)\)
= -g(x₁ + x₂) – f(y₁ + y₂)
= x₁x₂ + y₁y₂ + c (∵ from(2))
c + c’ = c + x₁x₂ + y₁y₂
= x₁x₂ + y₁y₂ + c
∴ 2gg’ + 2ff’ = c + c’
∴ The circles S = 0 and S’ = 0 are cut orthogonally.

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A De Moivre’s Theorem Important Questions Long Answer Type

Question 1.
State and prove De Moivre’s theorem for integral index. [May ‘03]
Solution:
Theorem : (De Moivre’s for integral index)
If n is an integer then
(cos θ + i sin θ)ⁿ = cos nθ + i sinnθ
Proof:
Case – 1:
Suppose ‘n’ is a positive integer
Let, S(n) be the statement that
(cos θ + i sin θ)ⁿ = cos nθ + i sin nθ
If n = 1 then
L.H.S: (cos θ + i sin θ)ⁿ
= (cos θ + i sin θ)¹
= cos θ + i sin θ
R.H.S: cos nθ +i sin nθ
= cos (1θ) + i sin (1θ)
= cos θ + i sin θ
∴ L.H.S = R.H.S
∴ S(1) is true.
Assume that S(k) is true
∴ (cos θ + i sin θ)^k = cos kθ + i sin kθ
Now,
(cos θ + i sin θ)^k+1 = (cos θ + i sin θ)^k (cos θ + i sin θ) .
= (cos kθ + i sin kθ) (cos θ + i sin θ)
= cos kθ cos θ + i cos kθ sin θ + i sin kθ cos θ – sin kθ sin θ
= (cos kθ cos θ – sin kθ sin θ) + i(sin kθ cos θ + cos kθ sin θ)
= cos (kθ + θ) + i sin(kθ + θ)
= cos(k + 1)θ + i sin(k + 1)θ
∴ S(k + 1) is true.
By the principle of mathematical induction S(n) is true, ∀ n ∈ N.

Case – 2 :
If n = 0 then
L.H.S: (cos θ + i sin θ)° = 1
R.H.S: cos nθ + i sin nθ = cos(0θ) + isin (0θ)
= cos θ + i sin θ
= 1 + i(0) = 1
∴ LH.S = R.H.S
∴ (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ.

Case – 3 :
Suppose ‘n’ is a negative integer
Let, n = – m where m ∈ Z⁺
L.H.S = (cos θ + i sin θ)
= (cos θ + i sin θ)^-m
= \(\frac{1}{(\cos \theta+i \sin \theta)^m}\)
= \(\frac{1}{\cos m \theta+i \sin m \theta}\) [∵ from case (1)]
= \(\frac{1}{\cos m \theta+i \sin m \theta} \times \frac{\cos m \theta-i \sin m \theta}{\cos m \theta-i \sin m \theta}\)
= \(\frac{\cos m \theta-i \sin m \theta}{\cos ^2 m \theta+\sin ^2 m \theta}\)
= \(\frac{\cos m \theta-i \sin m \theta}{1}\)
= cos mθ – i sin mθ
= cos (- m)θ + i sin(- m)θ
= cos nθ + i sin nθ
= R.H.S
∴ (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ, ∀ n ∈ Z.

Question 2.
If m, n are integers and x = cos α + i sin α, y = cos β + i sin β then prove that
x^myⁿ + \(\frac{1}{x^m y^n}\) = 2 cos (mα + nβ) and
x^myⁿ – \(\frac{1}{x^m y^n}\) = 2i sin (mα + nβ)
Solution:
Given that
x^m = (cos α + i sin α)^m
= cos mα + i sin mα = cis mα
yⁿ = (cos β + isin β)ⁿ
= cos nβ + i sin nβ = cis nβ
Now,
x^myⁿ = cis mα . cis nβ
= cis (mα + nβ)
= cos (mα + nβ) + i sin (mα + nβ)
\(\frac{1}{x^m y^n}=\frac{1}{\cos (m \alpha+n \beta)+i \sin (m \alpha+n \beta)}\)
= cos (mα + nβ) – i sin (mα + nβ)

(i) x^myⁿ + \(\frac{1}{x^m y^n}\)
= cos (mα + nβ) + i sin (mα + nβ) + cos (mα + nβ) – i sin (mα + nβ)
= 2 cos (mα + nβ)
∴ x^myⁿ + \(\frac{1}{x^m y^n}\) = 2 cos (mα + nβ)

(ii) x^myⁿ – \(\frac{1}{x^m y^n}\)
= cos (mα + nβ) + i sin (mα + nβ) – cos (mα + nβ) + i sin (mα + nβ)
= 2i sin (mα + nβ)
∴ x^myⁿ – \(\frac{1}{x^m y^n}\) = 2i sin (mα + nβ)

Question 3.
If n is a positive integer, show that (1 + i)ⁿ + (1 – i)ⁿ = \(2^{\frac{n+2}{2}} \cos \left(\frac{n \pi}{4}\right)\). [AP – Mar. 2015, Mar.’99]
Solution:

Let, 1 + i = r (cos θ + i sin θ)
then, r cos θ = 1, r sin θ = 1
∴ r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence.
√2 cos θ = 1,
cos θ = \(\frac{1}{\sqrt{2}}\)

√2 sin θ = 1
sin θ = \(\frac{1}{\sqrt{2}}\)

∴ θ lies in Q₁.
∴ θ = \(\frac{\pi}{4}\)

Similarly,
1 – i = √2 (cos \(\frac{\pi}{4}\) – i sin \(\frac{\pi}{4}\))
L.H.S:
(1 + i)ⁿ + (1 – i)ⁿ

Question 4.
If n is an integer then show that (1 + cos θ + i sin θ)ⁿ + (1 + cos θ – i sin θ)ⁿ = 2ⁿ⁺¹ cosⁿ \(\left(\frac{\theta}{2}\right)\) – i cos \(\left(\frac{n \theta}{2}\right)\) . [May ‘01, ‘97, March ’10. Mar. ’93, TS & AP – Mar. 2017]
Solution:

Question 5.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ, prove that cos² α + cos² β + cos² γ = \(\frac{3}{2}\) = sin² α + sin² β + sin² γ. [AP – Mar., May 2016; TS – Mar. ‘18. ‘15. May ‘15, May ‘09, March ‘03, ‘96, March ‘13 (old)]
Solution:
Given that,
cos α + cos β + cos γ = 0 = sin α + sin β + sin γ
Let, x = cos α + i sin α
y = cos β + i sin β
z = cos γ + i sin γ
Now,
x + y + z = cos α + i sin α + cos β + i sin β + cos γ + i sin γ
= (cos α + cos β + cos γ) + i(sin α + sin β + sin γ)
= 0 + i(0) = 0
∴ x + y + z = 0
Squaring on both sides,
(x + y + z)² = 0
x² + y² + z² + 2 (xy + yz + zx) = 0
x² + y² + z² = – 2 (xy + yz + zx)
= \(\frac{-2 x y z}{x y z}\) (xy + y + zx)
= – 2xyz \(\left(\frac{1}{z}+\frac{1}{x}+\frac{1}{y}\right)\)
= – 2xyz (cos γ – i sin γ + cos α – i sin α + cos β – i sin β)
= – 2xyz [(cos α + cos β + cos γ) – i (sin α + sin β + sin γ)]
= – 2xyz [0 – i . 0]
= – 2xyz(0) = 0
∴ x² + y² + z² = 0
(cos α + i sin α)² + (cos β + i sin β)² + (cos γ + i sin γ)² = 0
cos 2α + i sin2α + cos 2β + i sin 2β + cos 2γ + i sin 2γ = 0
(cos 2α + cos 2β + cos 2γ) + i(sin 2α + sin 2β + sin 2γ) = 0
Comparing real parts on both sides, we get
(i) cos 2α + cos 2β + cos 2γ = 0
2 cos² α – 1 + 2 cos² β – 1 + 2 cos² γ – 1 = 0
2 (cos² α + cos² β + cos² γ) = 3
cos² α + cos² β + cos² γ = \(\frac{3}{2}\)

(ii) 1 – sin² α + 1 – sin² β + 1 – sin² γ = \(\frac{3}{2}\)
3 – (sin² α + sin² β + sin² γ) = \(\frac{3}{2}\)
sin² α + sin² β + sin² γ = 3 – \(\frac{3}{2}\) = \(\frac{3}{2}\).

Question 6.
If n is an integer then show that (1 + i)²ⁿ + (1 – i)²ⁿ = 2ⁿ⁺¹ cos \(\frac{n \pi}{2}\) [May ’14. ’02, ’98, ’93, March ’09]
Solution:

Let, 1 + i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = 1,
cos θ = \(\frac{1}{\sqrt{2}}\)
√2 sin θ = 1
sin θ = \(\frac{1}{\sqrt{2}}\)
∴ θ lies in Q₁.
∴ θ = \(\frac{\pi}{4}\)
∴ 1 + i = √2 (cos \(\frac{\pi}{4}\) + i cos \(\frac{\pi}{4}\))
Similarly,
1 – i = √2 (cos \(\frac{\pi}{4}\) – i sin \(\frac{\pi}{4}\))
L.H.S:
(1 + i)²ⁿ + (1 – i)²ⁿ = [√2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))]²ⁿ + [√2 (cos \(\frac{\pi}{4}\) – i sin \(\frac{\pi}{4}\))]²ⁿ
= 2ⁿ (cos \(\frac{n \pi}{2}\) + i sin \(\frac{n \pi}{2}\)) + 2ⁿ (cos \(\frac{n \pi}{2}\) – i sin \(\frac{n \pi}{2}\))
= 2ⁿ [cos \(\frac{n \pi}{2}\) + i sin \(\frac{n \pi}{2}\) + cos \(\frac{n \pi}{2}\) – i sin \(\frac{n \pi}{2}\)]
= 2ⁿ . 2 cos \(\frac{n \pi}{2}\)
= 2ⁿ⁺¹ cos \(\frac{n \pi}{2}\)
= R.H.S
∴ (1 + i)²ⁿ + (1 – i)²ⁿ = 2ⁿ⁺¹ cos \(\frac{n \pi}{2}\).

Question 7.
If α, β are the roots of the equation x² – 2x + 4 = 0 then for any n ∈ N show that αⁿ + βⁿ = 2ⁿ⁺¹ cos \(\frac{n \pi}{3}\) [TS – May 2016; March ’14, ’11, May ’88, AP – Mar. 2019]
Solution:

Given quadratic equation is x² – 2x + 4 = 0
Comparing ax² + bx + c = 0 we get, a = 1, b = – 2, c = 4
∴ x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-(-2) \pm \sqrt{4-16}}{2(1)}\)
= \(\frac{2 \pm \sqrt{-12}}{2}\)
= \(\frac{2 \pm i 2 \sqrt{3}}{2}\)
= 1 ± √3i
Since, α, β are the roots of the equation
x² – 2x + 4 = 0 then
α = 1 + i√3, β = 1 – i√3
Let,
α = 1 + i√3 = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = √3
r = \(\sqrt{x^2+y^2}=\sqrt{(1)^2+(\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence,
2 cos θ = 1,
cos θ = \(\frac{1}{2}\)
2 sin θ = √3
sin θ = \(\frac{\sqrt{3}}{2}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{3}\)
α = 1 + i√3 = 2(cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\))
Similarly,
β = 1 – i√3 = 2(cos \(\frac{\pi}{3}\) – i sin \(\frac{\pi}{3}\))
L.H.S:

Question 8.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ then show that
(i) cos 3α + cos 3β + cos 3γ = 2 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 2 sin (α + β + γ)
(iii) cos (α + β) + cos (β + γ) + cos (γ + α) = 0
Soluton:
Given that,
cos α + cos β + cos γ = 0 = sin α + sin β + sin γ
Let,
x = cos α + i sin α
y = cos β + i sin β
z = cos γ + i sin γ
Now,
x + y + z = cos α + i sin α + cos β + i sin β + cos γ + i sin γ
= (cos α + cos β + cos γ) + i(sin α + sin β + sin γ)
= 0 + i (0) = 0
∴ x + y + z = 0
⇒ x³ + y³ + z³ = 3xyz
(cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ) = 3 (cos α + i sin α) (cos β + i sin β) (cos γ + i sin γ)
cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ = 3 cis α cis β cis γ
(cos 3α + cos 3β + cos 3γ) + i(sin 3α + sin 3β + sin 3γ) = 3 cis (α + β + γ)
= 3 [cos (α + β + γ) + i sin (α + β + γ)]

(i) Comparing the real parts on both sides we get,
cos 3α + i sin 3α + cos 3β = 3 cos (α + β + γ)

(ii) Comparing the imaginary parts on both sides we get,
sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)

(iii) Let,
x = cos α + i sin α
⇒ \(\frac{1}{x}\) = cos α – i sin α
y = cos β + i sin β
⇒ \(\frac{1}{y}\) = cos β – i sin β
z = cos γ + i sin γ
⇒ \(\frac{1}{z}\) = cos γ – i sin γ
Now,
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) = cos α – i sin α + cos β – i sin β + cos γ – i sin γ
= (cos α + cos β + cos γ) – i(sin α + sin β + sin γ)
= 0 + i(0) = 0
∴ \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) = 0
\(\frac{y z+x z+x y}{x y z}\) = 0
(cos α + i sin α) (cos β + i sin β) + (cos β + i sin β) (cos γ + i sin γ) + (cos γ + i sin γ) (cos α + i sin α) = 0
cis α cis β + cis β . cis γ + cis γ . cis α = 0
cis (α + β) + cis (β + γ) + cis (γ + α) = 0
cos (α + β) + i sin (α + β) + cos (β + γ) + isin (β + γ) + cos (γ + α) + isin (γ + α) = 0
[cos (α + β) + cos (β + γ) + cos (γ + α)] + i[sin (α + β) + sin (β + γ) + sin (γ + α)] = 0
Comparing real parts on both sides we get,
cos (α + β) + cos (β + γ) + cos (γ + α) = 0
Comparing imaginary parts on both sides
we get,
sin (α + β) + sin (β + γ) + sin (γ + α) = 0.

Question 9.
If n is an Integer and z = cis θ, (θ ≠ (2n + 1)\(\frac{\pi}{2}\)), then show that \(\frac{z^{2 n}-1}{z^{2 n}+1}\) = i tan nθ. [Mar. ’12. ’19(TS)]
Solution:
Given that,
z = cis θ = cos θ + i sin θ

Question 10.
Find all the roots of the equation x¹¹ – x⁷ + x⁴ – 1 = 0 [Board Paper].
Solution:
Given equation is x¹¹ – x⁷ + x⁴ – 1 = 0
x⁷ (x⁴ – 1) . 1 (x⁴ – 1) = 0
(x⁴ – 1) (x⁷ + 1) = 0
x⁴ – 1 = 0 or x⁷ + 1 = 0

x⁴ – 1 = 0:
x⁴ = 1
x = (1)^1/4
= (cos 0 + i sin 0)^1/4
= [cos (2kπ + 0) + isin(2kπ + 0)]^1/4
k = 0, 1, 2, 3
= [cos (2kπ) + i sin(2kπ]^1/4
= cos (\(\frac{k\pi}{2}\)) + sin (\(\frac{k\pi}{2}\))
= cis (\(\frac{k\pi}{2}\)), k = 0, 1, 2, 3
∴ The values of x are
cis (0), cis (\(\frac{\pi}{2}\)), cis π, cis (\(\frac{3\pi}{2}\)) : 1, i, – 1, – i

x⁷ + 1 = 0:
x⁷ = – 1
x = (- 1)^1/7
= [cos π + i sin π]
= [cos (2kπ + π) + i sin (2kπ + π)]^1/7, k = 0, 1, 2, 3, 4, 5, 6
= [cos (2k + 1)π + i sin (2k + 1)π]^1/7
= [cos (2k + 1)\(\frac{\pi}{7}\) + i sin (2k + 1)\(\frac{\pi}{7}\)]
= cis (2k + 1)\(\frac{\pi}{7}\), k = 0, 1, 2, 3, 4, 5, 6
The values of x are
cis \(\frac{\pi}{7}\), cis \(\frac{3 \pi}{7}\), cis \(\frac{5 \pi}{7}\), cis π, cis \(\frac{9 \pi}{7}\), cis \(\frac{11 \pi}{7}\), cis \(\frac{13 \pi}{7}\)
∴ The roots of the equation are ± 1, ± i, cis \(\frac{\pi}{7}\), cis \(\frac{3 \pi}{7}\), cis \(\frac{5 \pi}{7}\), cis π, cis \(\frac{9 \pi}{7}\), cis \(\frac{11 \pi}{7}\), cis \(\frac{13 \pi}{7}\)

Question 11.
Solve the equation x⁴ – 1 = 0.
Solution:
Given equation is x⁴ – 1 = 0
x⁴ = 1
x = (1)^1/4
= [cos o + i sin o]^1/4
= [cos (2kπ + 0) + i sin(2kπ + 0)]^1/4
k = 0, 1, 2, 3
= [cos 2kπ + i sin 2kπ]^1/4
= cos \(\frac{k \pi}{2}\) + i sin \(\frac{k \pi}{2}\)
= cis \(\frac{k \pi}{2}\), k = 0, 1, 2, 3
lf k = 0 then x = cos 0 + i sin 0 = 1 + i . 0 = 1
If k = 1 then x = cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\) = 0 + i . 1 = i
If k = 2 then x = cos π + i sin π
= – 1 + i .0 = – 1
If k = 3 then x cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\)
= o + i (- 1) = – i
∴ The roots of the given equation are ± 1, ± i.

Question 12.
Solve the equation x⁴ + 1 = 0. [May ’97]
Solution:
Given equation is x⁴ + 1 = 0
x⁴ = – 1
x = (- 1)^1/4
= [cos π + i sin π]^1/4
= [cos (2kπ + π) + i sin (2kπ + π)]^1/4, k = 0, 1, 2, 3
= [cos (2k + 1)π + i sin(2k + 1)π]^1/4
= cos(2k + 1) \(\frac{\pi}{4}\) + i sin(2k + 1) \(\frac{\pi}{4}\)
= cis (2k + 1) \(\frac{\pi}{4}\), k = 0, 1, 2, 3
If k = 0, x = cis \(\frac{\pi}{4}\)
If k = 1, x = cis \(\frac{3 \pi}{4}\)
If k = 2, x = cis \(\frac{5 \pi}{4}\)
If k = 3, x = cis \(\frac{7 \pi}{4}\)
∴ The roots of the given equation are cis \(\frac{\pi}{4}\), cis \(\frac{3 \pi}{4}\), cis \(\frac{5 \pi}{4}\), cis \(\frac{7 \pi}{4}\).

Question 13.
If n is a positive integer, show that (p + iq)^1/n + (p – iq)^1/n = 2(p² + q²)^1/2n . cos \(\left(\frac{1}{n} \tan ^{-1} \frac{q}{p}\right)\) [AP – Mar. 18, May ’15; Mar. ’01]
Solution:
Let p + iq = r (cos θ + i sin θ)
then r cos θ = p, r sin θ = q
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{\mathrm{p}^2+\mathrm{q}^2}\)
Hence,
\(\sqrt{p^2+q^2}\) cos θ = p, \(\sqrt{p^2+q^2}\) sin θ = q
cos θ = \(\frac{p}{\sqrt{p^2+q^2}}\)
sin θ = \(\frac{q}{\sqrt{p^2+q^2}}\)
∴ tan θ = \(\frac{\sin \theta}{\cos \theta}=\frac{\frac{q}{\sqrt{p^2+q^2}}}{\frac{p}{\sqrt{p^2+q^2}}}=\frac{q}{p}\)
θ = \(\tan ^{-1}\left(\frac{q}{p}\right)\)
∴ p + iq = \(\sqrt{p^2+q^2}\) [cos θ + i sin θ]
Similarly,
p – iq = \(\sqrt{p^2+q^2}\) [cos θ – i sin θ]

Question 14.
Show that one value of \(\left[\frac{1+\sin \frac{\pi}{8}+i \cos \frac{\pi}{8}}{1+\sin \frac{\pi}{8}-i \cos \frac{\pi}{8}}\right]^{\frac{8}{3}}\) is – 1. [TS – Mar. 2016; May ’12, May ’10]
Solution:
Given,

Question 15.
Solve (x – i)ⁿ = xⁿ, n is a positive integer. [March ’02]
Solution:
Given equation is (x – 1)ⁿ = xⁿ
Taking nth root of each side of (x – 1)ⁿ = xⁿ
we have
x – 1 = x(1)^1/n
= x [cos 0 – i sin 0]^1/n
= x [cos (2kπ + 0) + i sin (2kπ + 0)]^1/n
k = 0, 1, ………….., (n – 1)
= x [cos 2kπ + i sin 2kπ]^1/n

Some More Maths 2A De Moivre’s Theorem Important Questions

Question 1.
Find the value of (1 + i√3)³.
Solution:

Let 1 + i√3 = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = √3
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{(1)^2+(\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence,
2 cos θ = 1, 2 sin θ = √3
cos θ = \(\frac{1}{2}\), sin θ = \(\frac{\sqrt{3}}{2}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{3}\)
∴ 1 + i√3 = 2 (cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\))
Now,
(1 + i√3)³ = [2 (cos \(\frac{\pi}{3}\) + i sin \(\frac{\pi}{3}\))]³
= 8 (cos π + i sin π)
= 8 (- 1 + i . 0) = – 8.

Question 2.
If (1 + x)ⁿ = a₀ + a₁x + a₂x² + ………….. + a_nxⁿ, then show that
(i) a₀ – a₂ + a₄ – a₆ + ……. = 2^n/2 cos \(\frac{n \pi}{4}\)
(ii) a₁ – a₃ + a₅ + ……………. = 2^n/2 sin \(\frac{n \pi}{4}\)
Solution:
Given,
(1 + x)ⁿ = a₀ + a₁x + a₂x² + ……………. + a_nxⁿ
Put x = i then
(1 + i)ⁿ = a₀ + a₁(i) + a₂i² + a₃i³ + a₄i⁴ + a₅i⁵ + …………… + a_niⁿ
= a₀ + a₁i – a₂ – a₃i – a₄ + a₅i + …………. + a_niⁿ
= (a₀ – a₂ + a₄ – a₆ + …………. ) + i(a₁ – a₃ + a₅ – …………) ……………..(1)
Let, 1 + i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = i
cos θ = \(\frac{1}{\sqrt{2}}\)
√2 sin θ = 1
sin θ = \(\frac{1}{\sqrt{2}}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{4}\)
∴ (1 + i) = √2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))
(1 + i)ⁿ = [√2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))]ⁿ
= 2^n/2 (cos \(\frac{n \pi}{4}\) + i sin \(\frac{n \pi}{4}\))
From (1),
2^n/2 (cos \(\frac{n \pi}{4}\) + i sin \(\frac{n \pi}{4}\)) = (a₀ – a₂ + a₄ – a₆ + ……………….) + i (a₁ – a₃ + a₅ – ………….)

(i) Comparing real parts on both sides we get,
a₀ – a₂ + a₄ – a₆ + ………………. = 2^n/2 cos \(\frac{n \pi}{4}\)

(ii) Comparing imaginary parts on bothsides we get,
a₁ – a₃ + a₅ – …………… = 2^n/2 sin \(\frac{n \pi}{4}\).

Question 3.
Solve the equation x⁵ + 1 = 0.
Solution:
Given equation is x⁵ + 1 = 0
x⁵ = – 1
x = (- 1)^1/5
= [cos π + i sin π]^1/5
= [cos(2kπ + π) + i sin (2kπ + π)]^1/5, k = 0, 1, 2, 3, 4
= [cos(2k + 1)π + i sin (2k + 1)π]^1/5
= cis (2k + 1) \(\frac{\pi}{5}\), k = 0, 1, 2, 3, 4
If k = 0,
⇒ x = cis \(\frac{\pi}{5}\)

If k = 1,
⇒ x = cis \(\frac{3 \pi}{5}\)

If k = 2,
⇒ x = cis π

If k = 3,
⇒ x = cis \(\frac{7 \pi}{5}\)

If k = 4,
⇒ x = cis \(\frac{9 \pi}{5}\)
∴ The roots of the given equation are cis \(\frac{\pi}{5}\), cis \(\frac{\pi}{5}\), cis π, cis \(\frac{7 \pi}{5}\), cis \(\frac{9 \pi}{5}\).

Question 4.
Solve the equation x⁹ – x⁵ + x⁴ – 1 = 0.
Solution:
Given equation is x⁹ – x⁵ + x⁴ – 1 = 0
x⁵ (x⁴ – 1) + 1 (x⁴ – 1) = 0
(x⁴ – 1) (x⁵ + 1) = 0
x⁴ – 1 = 0 or x⁵ + 1 = 0

x⁴ – 1 = 0:
x⁴ = 1
x = (1)^1/4
= [cos 0 + i sin 0]^1/4
= [cos (2kπ + 0) + i sin (2kπ + 0)]^1/4, k = 0, 1, 2, 3
= [cos (2kπ) + i sin(2kπ)]^1/4
= cos \(\frac{k \pi}{2}\) + i sin \(\frac{k \pi}{2}\)
= cis \(\frac{k \pi}{2}\), k = 0, 1, 2, 3
If k = 0
⇒ x = cos 0 + i sin 0
= 1 + i . 0 = 1
If k = 1
⇒ x= cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
= 0 + i . 1 = 1
If k = 2
⇒ x = cos π + i sin π
= – 1 + i . 0 = – 1
If k = 3x
⇒ x = cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\)
= 1 + i(- 1) = – i
∴ The values of x are ± 1, ± 1.

x⁵ + 1 = 0:
x⁵ = (- 1)
x = (- 1)^1/5
= [cos π + i sin π]^1/5
= [cos (2kπ + π) + i sin(2kπ + π)]^1/5, k = 0, 1, 2, 3, 4
= [cos(2k + 1)π + i sin(2k + 1)π]^1/5
= cos (2k + 1) \(\frac{\pi}{5}\) + i sin(2k + 1) \(\frac{\pi}{5}\)
= cis (2k + 1) \(\frac{\pi}{5}\), k = 0, 1, 2, 3, 4
If k = 0
⇒ x = cis \(\frac{\pi}{5}\)
If k = 1
⇒ x = cis \(\frac{3 \pi}{5}\)
If k = 2
⇒ x = cis π
If k = 3
⇒ x = cis \(\frac{7 \pi}{5}\)
If x = 4
⇒ x = cis \(\frac{9 \pi}{5}\)
∴ The values of x are cis \(\frac{\pi}{5}\), cis \(\frac{3 \pi}{5}\), cis π, cis \(\frac{7 \pi}{5}\), cis \(\frac{9\pi}{5}\).
∴ The roots of the given equation are ± 1, ± i, cis \(\frac{\pi}{5}\), cis \(\frac{3 \pi}{5}\), cis π, cis \(\frac{7 \pi}{5}\), cis \(\frac{9\pi}{5}\).

Question 5.
Find the common roots of x¹² – 1 = 0 and x + x + 1 = 0.
Solution:
Given equation is x¹² – 1 = 0
x¹² = 1
x = (1)¹²
= [cos 0 + i sin 0]^1/12
= [cos (2kπ + 0) + i sin (2kπ + 0)]^1/12, k = 0, 1, ……………, 11
= [cos 2kπ + i sin 2kπ]^1/12
= cos \(\frac{k \pi}{6}\) + i sin \(\frac{k \pi}{6}\)
= cis \(\frac{k \pi}{6}\), k = 0, 1, 2, …………., 11
If k = 0
⇒ x = cis 0
If k = 1
⇒ x = cis \(\frac{\pi}{6}\)
If k = 2
⇒ x = cis \(\frac{\pi}{3}\)
If k = 3
⇒ x = cis \(\frac{\pi}{2}\)
If k = 4
⇒ x = cis \(\frac{2 \pi}{3}\)
If k = 5
⇒ x = cis \(\frac{5 \pi}{6}\)
If k = 6
⇒ x = cis π
If k = 7
⇒ x = cis \(\frac{7 \pi}{6}\)
If k = 8
⇒ x = cis \(\frac{4 \pi}{3}\)
If k = 9
⇒ x = cis \(\frac{3 \pi}{2}\)
If k = 10
⇒ x = cis \(\frac{5 \pi}{3}\)
If k = 11
⇒ x = cis \(\frac{11 \pi}{6}\)
∴ Therootsof x¹² – 1 = 0 are cis 0, cis \(\frac{\pi}{6}\), cis \(\frac{\pi}{3}\), cis \(\frac{\pi}{2}\), cis \(\frac{2 \pi}{3}\), cis \(\frac{5 \pi}{6}\), cis π, cis \(\frac{7 \pi}{6}\), cis \(\frac{4 \pi}{3}\), cis \(\frac{3 \pi}{2}\), cis \(\frac{5 \pi}{3}\), cis \(\frac{11 \pi}{6}\)

Given equation is x⁴ + x² + 1 = 0
Multiplying on both sides with x² – 1
we get,
(x² – 1) (x⁴ + x² + 1) = 0
x⁶ – 1 = 0
x⁶ = 1
x = (1)^1/6
= [cos 0 + i sin 0]^1/6
= [cos (2kπ + 0) + i sin (2kπ + 0)]^1/6, k = 0, 1, 2, 3, 4, 5
= [cos 2kπ + i sin 2kπ]^1/6
= cos \(\frac{k \pi}{3}\) + i sin \(\frac{k \pi}{3}\)
= cis \(\frac{k \pi}{3}\), k = 0, 1, 2, 3, 4, 5
If k = 0
⇒ x = cis 0
If k = 1
⇒ x = cis \(\frac{\pi}{3}\)
If k = 2
⇒ x = cis \(\frac{2 \pi}{3}\)
If k = 3
⇒ x = cis π
If k = 4
⇒ x = cis \(\frac{4 \pi}{3}\)
If k = 5
⇒ x = cis \(\frac{5 \pi}{3}\)
The values of given equation are cis 0, cis \(\frac{\pi}{3}\), cis \(\frac{2 \pi}{3}\), cis π, cis \(\frac{4 \pi}{3}\), cts \(\frac{5 \pi}{3}\).
∴ The common roots of the given equations are cis \(\frac{\pi}{3}\), cis \(\frac{2 \pi}{3}\), cis \(\frac{4 \pi}{3}\), cis \(\frac{5 \pi}{3}\).

Question 6.
Find the number of 15th roots of unity, which are also 25th roots of unity.
Solution:
15th roots of unity:
Let, x = \(\sqrt[15]{1}=(1)^{1 / 15}\)
= [cos 0 + i sin 0]^1/15
= [cos (2nπ + 0) + i sin(2nπ + 0)]^1/15
n = 0, 1, 2, …………., 14
= [cos 2nπ + i sin 2nπ]^1/15
= \(\cos \frac{2 n \pi}{15}+i \sin \frac{2 n \pi}{15}\)
= cis \(\frac{2n \pi}{15}\), n = 0, 1, 2, …………….., 14

25th roots of unity:
Let, x = \(\sqrt[25]{1}\)
= (1)^1/25
= [cos 0 + i sin 0]^1/25
= [cos (2mπ + 0) + i sin (2mπ + 0)]^1/25
m = 0, 1, 2, ………….., 24
= [cos 2mπ + i sin 2mπ]^1/25
= cos \(\frac{2 \mathrm{~m} \pi}{25}\) + i sin \(\frac{2 \mathrm{~m} \pi}{25}\)
= cis \(\frac{2 \mathrm{~m} \pi}{25}\), m = 0, 1, 2, ……………., 24

∴ The common roots are cis 0, cis \(\frac{2 \pi}{5}\), cis \(\frac{4 \pi}{5}\), cis \(\frac{6 \pi}{5}\), cis \(\frac{8 \pi}{5}\).
∴ The number of common roots = 5 (or)
The GCM of 15 and 25 is

Question 7.
Find the product of all the values of (1 + i)^4/5.
Solution:

Let, 1 + i = r (cos θ + i sin θ)
then r cos θ = 1, r sin θ = 1
r = \(\sqrt{x^2+y^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = i,
cos θ = \(\frac{1}{\sqrt{2}}\)
√2 sin θ = 1
sin θ = \(\frac{1}{\sqrt{2}}\)
∴ θ lies in the Q₁.
∴ θ = \(\frac{\pi}{4}\)
∴ 1 + i = √2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))
Now,
(1 + i) = [√2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))]⁴
= 4 (cos π + i sin π)
= 4[cos(2kπ + π) + i sin (2kπ + π)]
= 4[cos(2k + 1)π + isin(2k + 1)π]
(1 + i)^4/5 = 4^1/5 [cos(2k + 1)π + isin(2k + 1)π]^1/5
k = 0, 1, 2, 3, 4
= 4^1/5 [cos (2k + 1) \(\frac{\pi}{5}\) + i sin (2k + 1) \(\frac{\pi}{5}\)]
= 4^1/5 cis (2k + 1) \(\frac{\pi}{4}\), k = 0, 1, 2, 3, 4

= 4 cis (5π)
= 4 cis π
= 4 (cos π + i sin π)
= 4 [- 1 + i . 0] = – 4.

Question 8.
If z² + z + 1 = 0, where z is a complex number, prove that
\(\left(z+\frac{1}{z}\right)^2+\left(z^2+\frac{1}{z^2}\right)^2+\left(z^3+\frac{1}{z^3}\right)^2\) + \(\left(z^4+\frac{1}{z^4}\right)^2+\left(z^5+\frac{1}{z^5}\right)^2+\left(z^6+\frac{1}{z^6}\right)^2\) = 12.
Solution:
Given equation is z² + z + 1 = 0
Comparing with ax² + bx + c we get, a = 1, b = 1, c = 1
The roots of the given equation is
z = \(\frac{-\mathrm{b} \pm \sqrt{\mathrm{b}^2-4 \mathrm{ac}}}{2 \mathrm{a}}=\frac{-1 \pm \sqrt{1-4 \cdot 1 \cdot 1}}{2(1)}\)
= \(\frac{-1 \pm \sqrt{1-4}}{2} \Rightarrow \frac{-1 \pm \sqrt{3} i}{2}\) = ω, ω²
Let, z = ω
L.H.S:

= (ω + ω²)² + (ω² + ω) + 4 + (ω + ω²) + (ω² + ω)² + 4
= (- 1)² + (- 1)² + 4 + (- 1)² + (- 1)² + 4
= 1 + 1 + 4 + 1 + 1 + 4
= 12 = R.H.S.

Question 9.
Prove the sum of 99th power of the roots of the equation x⁷ – 1 = 0 is zero and hence deduce the roots of x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = o.
Solution:
Given equation is x⁷ – 1 = 0
x⁷ = 1
x = (1)^1/7
= [cos 0 + i sin 0]^1/7
= [cos (2kπ + 0) + i sin(2kπ + 0)]^1/7
k = 0, 1, 2, 3, …………….., 6
= [cos 2kπ + i sin 2kπ]^1/7
= cos \(\frac{2 \mathrm{k} \pi}{7}\) + i sin \(\frac{2 \mathrm{k} \pi}{7}\)
= cis \(\frac{2 \mathrm{k} \pi}{7}\), k = 0, 1, 2, …………, 6
If k = 0
⇒ cis 0 = x
If k = 1
⇒ cis \(\frac{2 \pi}{7}\) = x
If k = 2
⇒ cis \(\frac{4 \pi}{7}\) = x
If k = 3
⇒ cis \(\frac{6 \pi}{7}\) = x
If k = 4
⇒ cis \(\frac{8 \pi}{7}\) = x
If k = 5
⇒ cis \(\frac{10 \pi}{7}\) = x
If k = 6
⇒ cis \(\frac{12 \pi}{7}\) = x
∴ All the values of x⁷ – 1 = 0 are cis 0, cis \(\frac{2 \pi}{7}\), cis \(\frac{4 \pi}{7}\), cis \(\frac{6 \pi}{7}\), cis \(\frac{8 \pi}{7}\), cis \(\frac{10 \pi}{7}\), cis \(\frac{12 \pi}{7}\)
The 99th power of the roots of the equation x⁷ – 1 = 0 are

= 1 + ω + ω² + ω³ + ω⁴ + ω⁵ + ω⁶
= 0 (from theorem)
Given equation is
x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = 0
Multiplying on both sides with (x – 1)
(x – 1) (x⁶ + x⁵ + x⁴ + x³ + x² + x + 1) = 0
x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x – x⁶ – x⁵ – x⁴ – x³ – x² – x – 1 = 0
x⁷ – 1 = 0
x = 1 is also a root of x⁷ – 1 = 0.
∴ The roots of the equation x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = 0 are x = cis \(\frac{2k \pi}{7}\), k = 1, 2, 3, ………., 6.

Students can go through TS Inter 2nd Year Chemistry Notes 13th Lesson Organic Compounds Containing Nitrogen will help students in revising the entire concepts quickly.

TS Inter 2nd Year Chemistry Notes 13th Lesson Organic Compounds Containing Nitrogen

→ Amines can be considered as derivatives of ammonia obtained by replacement of one, two or all the three hydrogen atoms by alkyl and / or aryl groups.

→ The amines are classified as primary (1°), secondary (2°) or tertiary (3°) amines. They are represented by the general formulas RNH2 (Primary amines), R₂NH or RNHR’ (Secondary amines) as R₃N or R NR’ R” or R₂ NR’ (Tertiary amines).

→ All the three types of amines behave as Lewis bases due to the presence of one unshared electron pair on nitrogen atom.

→ Amines are obtained from nitrocompounds, halides, amides, imides etc.

→ Primary and secondary amines are involved in intermolecular association due to inter- molecular hydrogen bonding. Tertiary amines have no intermolecular hydrogen bonding due to the absence of H-atom on nitrogen. Hence the boiling points of isomeric amines are in the order.
1° > 2° > 3°

→ The order of basicity of amines in the gaseous phase follows the order :
3° > 2° > 1° > NH₃

→ In aqueous solution the order of basicity of substituted amines is
(CH₃)₂ NH > CH₃ NH₂ > (CH₃)₃ N > NH₃
(C₂H₅)₂ NH > (C₂H₅)₃N > C₂H₅NH₂ > NH₃

→ Aliphatic and aromatic primary amines on heating with chloroform and ethanolic KOH form isocyanide or carbylamine which are foul smelling substances. Secondary and tertiary amines do not give this reaction.

→ Benzene sulphonyl chloride (C₆H₅.S0₂Cl) is known as Hinsberg’s reagent. It is used to distinguish between primary, secondary and tertiary amines and also to separate the amines from their mixture.

→ -NH₂ group is ortho and para directing and a powerful activating group in electrophilic substitution reactions of aniline.

→ Diazonium salts have the general formula
R N₂ X where R stands for an aryl group and X ion may be Cl, B̅r̅, HS̅O̅₄ , BF̅₄ etc.

→ Diazonium salts are very good intermediates for the introduction of – F, – Cl, – Br, – I, – CN, – OH, – NO₂ groups into the aromatic ring.

→ Alkyl cyanides are alkyl derivatives of hydrogen cyanide and isocyanides are isomers of alkyl cyanides.

→ Alkyl cyanides are usually obtained from alkyl halides, aldoximes and amides. Alkyl isocyanides are formed from alkyl halides by reacting with silver cyanide. Alkyl cyanides are used as intermediates in the multistep organic synthesis.

Students can go through TS Inter 2nd Year Chemistry Notes 12th Lesson Organic Compounds Containing C, H and O will help students in revising the entire concepts quickly.

TS Inter 2nd Year Chemistry Notes 12th Lesson Organic Compounds Containing C, H and O

→ An alcohol contains one or more hydroxyl (- OH) group(s) directly attached to carbon atom(s), of an aliphatic system. A phenol contains – OH group(s) directly attached to carbon atom(s) of an aromatic system.

→ Ethers are compounds formed by substituting the hydrogen atom of hydroxyl group of an alcohol or phenol by an alkyl or aryl, group.

→ Alcohols and phenols may be classified as mono-, di-, tri or polyhydric compounds depending on whether they contain one, two, three or many – OH groups respectively.

→ Primary (1°), Secondary (2°) and tertiary (3°) alcohols may be shown as given below:

→ In allylic alcohols, the – OH group is attached to an sp3 hybridised carbon next to the carbon-carbon double bond.
Ex : CH₂ = CH – CH₂OH (Allyl alcohol)

→ In benzylic alcohols, the – OH group is atta-ched to a sp3-hybridised carbon atom next to an aromatic ring.
Ex: C₆H₅CH₂OH (Benzyl alcohol)

→ In vinylic alcohols, the – OH group is bonded to a carbon-carbon double bond.
Ex: CH₂ = CH – OH (Vinyl alcohol)

→ Ethers are classified as

• Simple or sym-metrical and
• Mixed or unsymmetrical.

In simple ethers, the alkyl or aryl groups attached to the oxygen atom are the same.
Ex : C₂H₅OC₂H₅, Diethyl ether.
In mixed ethers, the two alkyl or aryl groups are different.
Ex: Anisole, C₆H₅OCH₃.

→ Cresols are substituted phenols having methyl groups in the ortho, meta or para positions.

→ Dihydroxy derivatives of benzene :

→ Alkenes react with water in the presence of acid to form alcohols. In unsymmetrical alkenes the addition of water takes place according to Markonikoff’s rule.

→ Alcohols are also prepared by hydro bora- tion – oxidation of alkenes. The addition of water to the alkene follows anti-Markoni- koff’s rule.

→ Aldehydes and ketones are reduced to the corresponding alcohols by addition of hydrogen in the presence of metal catalysts. However, many of the catalysts used (Pt, Pd, Ru, Rh) are relatively expensive and that other functional groups also react (C = C, – C = C – – NO₂, – C = NT).

→ Carboxylic acids are reduced to 10 alcohols in excellent yield by lithium aluminium hydride.

→ Alcohols are produced by the reaction of Grignard reagents with aldehydes and ketones. The reaction produces a 1 ° alcohol with methanal (formaldehyde), a 2° alcohol with other aldehydes and 3° alcohol with ketones.

→ Phenol is prepared from chloro benzene first by fusion with NaOH at 623 K and 320 atmospheres pressure, followed by acidification of the sodium phenoxide produced.

→ Diazonium salts are hydrolysed to phenols by warming with water or by treating with dilute acids.

→ Solubility of alcohols and phenols in water is due to their ability to form hydrogen bonds with water molecules.

→ Alcohols and phenols react with active metals such as Na, K and Al to yield corresponding alkoxides / phenoxides and hydrogen. Phenols react with NaOH to form sodium phenoxides.

→ In substituted phenols, the presence of electron withdrawing groups such as nitro group, enhances the acidic strength of phenol. On the other hand, electron releasing groups decrease the acid strength.

→ Lucas reagent (Cone. HCl and ZnCl is used to distinguish between primary, secondary and tertiary alcohols. At room temperature, tertiary alcohols react immediately with Lucas reagent producing turbidity in the reaction mixture, the secondary alcohols give turbidity within 5 to 10 minutes and the primary alcohols do not give turbidity at all at room temperature.

→ With Cone. HNOs, phenol is converted to 2, 4, 6 – trinitrophenol which is known as picric acid.

→ When phenol is treated with bromine water, a white precipitate of 2, 4, 6- tribromo phenol is formed.

→ Sodium phenoxide on reaction with carbon dioxide followed by acidification gives salicylic acid.

→ On treating phenol with chloroform in the presence of NaOH, a -CHO group is introduced at ortho position of the benzene ring. This reaction is called Reimer-Tiemann reaction.

→ Methanol, CH₃OH, is known as ‘wood spirit’. Methanol is produced by catalytic hydrogenation of carbon monoxide at high pressure and temperature in the presence of ZnO, Cr₂O₃ catalyst.

→ Ethanol, C₂H₅OH is obtained commercially by fermentation of sugars.

→ Ethoxy ethane (diethyl ether) is obtained when ethanol is dehydrated with Cone. H₂SO₄ at 413 K.

→ Williamson synthesis is an important method for the preparation of symmetrical and unsymmetrical ethers.

→ The C – O bond in ethers is polar and hence, ethers have a net dipole moment.

→ The boiling points of ethers resemble those of alkanes while their solubility is comparable to those of alcohols having the same molecular mass.

→ The alkoxy group (- OR) in alkyl ary ethers is ortho, para directing and activates the aromatic ring towards electrophilic substitution.

→ Aldehydes and ketones are the simplest and most important carbonyl compounds

→ Aldehydes and ketones are often called by their common names instead of IUPAC names.

→ The IUPAC names of open chain aliphatic aldehydes and ketones are derived from the names of the corresponding alkanes by replacing the ending – e with – al and – one respectively.

→ The carbonyl carbon atom is sp² – hybridised and forms three sigma (σ) bonds. The fourth valence electron of carbon remains in its p-orbital. This p-orbital forms a π – bond with oxygen by overlap with p-orbital of an oxygen.

→ Aldehydes and ketones are generally pre-pared by oxidation of primary and secondary alcohols respectively.

→ Ozonolysis of alkenes followed by reaction with zinc dust and water gives aldehydes, ketones or a mixture of both depending on the substitution pattern of the alkene.

→ Acyl chloride is hydrogenated over a catalyst, Pd over BaSO₄. This reaction is called Rosen-mund reduction.

→ Nitriles are reduced to corresponding ami¬nes with stannous chloride and HC/, which on hydrolysis give corresponding aldehydes. This reaction is called Stephen reaction.

→ Strong oxidising agents, for example potas-sium permanganate, oxidise toluene and its derivatives to benzoic acid.

→ Chromyl chloride, a mild oxidising agent, oxidises the methyl group of toluene to a chromium complex which on hydrolysis gives benzaldehyde. This reaction is called Etard reaction.

→ Side chain chlorination of toluene gives benzalchloride which on hydrolysis gives benzaldehyde.

→ Benzaldehyde and substituted benzaldehyde can be prepared by Guttermann-Koch reaction.

→ When benzene or its derivative is treated with carbon monoxide hydrogen chloride in the presence of anhydrous aluminium chloride or cuprous chloride, it gives benzaldehyde or substituted benzaldehyde.

→ When benzene or substituted benzene is treated with acid chloride in the presence of anhydrous AlCl3, it gives the corresponding ketone. This reaction is known as Friedel Crafts acylation.

→ Alkenes undergo electrophilic addition reactions whereas aldehydes and ketones undergo nucleophilic addition reactions.

→ Aromatic carboxylic acids can be prepared by vigorous oxidation of alkyl benzenes with chromic acid or acidic or alkaline KMnO₄. The side chain, irrespective of its length, is oxidised to – COOH.

→ Aldehydes and ketones undergo nucleophilic addition reactions with hydrogen cyanide, sodium bisulphite, Grignard reagents and alcohols. They also undergo addition- elimination reactions with ammonia and its derivatives.

→ Carboxylic acids have higher boiling points than aldehydes, ketones and alcohols of comparable molecular masses. This is due to more extensive association of carboxylic acid molecules through intermolecular hydrogen bonding.

→ Aldehydes and ketones are reduced to primary and secondary alcohols respectively by sodium borohydride (NaBH₄) or lithium aluminium hydride (Li AlH₄) as well as by catalytic hydrogenation.

→ Carboxylic acids are more acidic than phenols because the carboxylate ion is more stabilised than phenoxide ion.

→ Carboxylic acids on heating with sulphuric acid or P₂O₅ give corresponding anhydride. Thus acetic acid gives acetic anhydride (ethanoic anhydride) when heated with H₂SO₄ or P₂O₅.

→ The group of aldehydes and ketones is reduced to CH, group on treatment with Zinc-amalgam and concentrated HCl (Clemmensen reduction) or with hydrazine – followed by heating with NaOH or KOH in high boiling solvent like ethylene glycol (Wolff-Kishner reduction).

→ Carboxylic acids give esters when heated with alcohols or phenols in the presence of concentrated H₂SO₄ or HCl gas as catalyst.

→ Aldehydes are easily oxidised to carboxylic acids having the same number of carbon atoms. Ketones are generally oxidised under vigorous conditions to give a mixture of carboxylic acids having less number of carbon atoms than the parent ketone.

→ HVZ reaction – carboxylic acids having an α-hydrogen are halogenated at the α – position on treatment with chlorine (or) Bromine in the present of small amount of red phosphorus to give α – halo carboxylic acids.

→ Methyl ketones can be distinguished from other ketones by iodoform test.

→ Aromatic carboxylic acids undergo electrophilic substitution reactions in which the carboxyl group acts as a deactivating and meta-directing group.

Students can go through TS Inter 2nd Year Chemistry Notes 11th Lesson Haloalkanes and Haloarenes will help students in revising the entire concepts quickly.

TS Inter 2nd Year Chemistry Notes 11th Lesson Haloalkanes and Haloarenes

→ Alkyl/aryl halides may be classified as mono, di or polyhalogen (tri-tetra, etc) compounds depending upon whether they contain one, two or more halogen atoms in their structures.

→ Halogen compounds containing sp³ C – X bond (X = F, Cl, Br, I) include Alkyl halides (haloalkanes), Allylic halides and Benzylic halides.

→ Alkyl halides are further classified as pri-mary (1°). secondary (2°) or tertiary (3°) according to the nature of the carbon to which the halogen is attached.

→ Halogen compounds containing sp² C – X bond include Vinylic halides and Aryl halides.

→ Dihaloalkanes are called geminal (gem) halides if halogen atoms are present in the same carbon atom and vicinal (vie) halides if halogen atoms are present on adjacent carbon atoms.

→ Since halogen atoms are more electronegative than carbon, the carbon-halogen bond of alkyl halide is polarised.

→ C – X bond length increases from C – F to C – I.

→ Alkyl halides are prepared from alcohols on reaction with concentrated halogen acids (HX), PCl₃, PCl₅ Or SOCl₂.

→ Free radical chlorination or bromination of alkanes gives a complex mixture of isomeric mono and polyhaloalkanes.

→ Aryl chlorides or bromides can be prepared by reaction of the hydrocarbon with chlorine or bromine at room temperature in the presence of halogen carrier like Fe, AlCl₃ or SbCl₅.

→ When an aromatic primary amine reacts with nitrous acid (NaNO₂ + HX) at 0 – 5°C, a diazonium salt is formed. The diazonium salt solution reacts with cuprous chloride or cuprous bromide-, the diazonium group is replaced by – Cl or – Br. This reaction is known as Sandmeyer s reaction.

→ When diazonium salt solution is shaken with KI solution the diazonium group is replaced by iodine.

→ Addition of bromine in CCl₄ to an alkene results in discharge of reddish brown colour of bromine. This is an important test for the detection of unsaturation in a molecule.

→ Alkyl fluoride is prepared by heating an alkyl chloride or bromide in the presence of a metallic fluoride such as AgF₂, Hg₂F₂ etc (swarts reaction).
CH₃Br + AgF → CH₃F + AgBr

→ Haloalkanes are only very slightly soluble in water.

→ The chemical reactions of haloalkanes may be divided into three categories.

• Nucleophilic substitution
• Elimination reactions
• Reaction with metals.

→ The order of reactivity of alkyl halides towards S_N¹ and S_N² reactions is as follows :

• For S_N² reaction : CH₃X > primary halide > secondary halide > tertiary halide.
• For S_N¹ reaction: tertiary halide > secondary halide > primary halide > CH₃X.

→ A carbon atom joined to four different atoms or groups is called an asymmetric carbon or stereocentre or chirality centre.

→ The objects which are non-superimposable on their mirror images are said to be chiral and this property is known as chirality. Objects which are superimposable on their mirror images are called achiral.

→ Optical activity is the ability of a chiral sub-stance to rotate the plane of plane-polarised light.

→ The three dimensional arrangement of atoms or groups at a chirality centre is called the absolute configuration.

→ The stereoisomers related to each other as non-superimposable mirror images are called enantiomers.

→ S_N² reactions of optically active alkyl halides are accompanied by inversion of configuration.

→ S_N¹ reactions of optically active alkyl halides are accompanied by racemisation.

→ Zaitsev rule (Saytzef rule) : “In dehydro- halogenation reactions, the preferred product is that alkene which has greater number of alkyl groups attached to the doubly bonded carbon atoms”.

→ Alkyl magnesium halides (RMgX) are known as Grignard reagents.

→ A number of polyhalogen compounds e.g., dichloromethane, chloroform, iodoform, CCl₄, freon and DDT have many industrial applications.

→ Chloroform is slowly oxidised by air in the presence of light to a very poisonous gas, carbonyl chloride, also known as phosgene, COCl₂. Hence chloroform is stored in closed amber coloured bottles completely filled so that air is kept out.

→ Dichlorodifluoro methane (CCl₂F₂) is known as Freon 12.

→ Paul Muller discovered the effectiveness of DDT as an insecticide.

Students can go through TS Inter 2nd Year Chemistry Notes 10th Lesson Chemistry in Everyday Life will help students in revising the entire concepts quickly.

TS Inter 2nd Year Chemistry Notes 10th Lesson Chemistry in Everyday Life

→ Drugs are chemicals of low molecular masses ( ~ 100 to 500 u) which interact with macro- molecular targets and produce a biological response.

→ Drugs are called medicines when their biological response is therapeutic and useful.

→ Use of chemical for therapeutic effect is called chemotherapy.

→ Drugs are classified on the basis of

• Pharmacological effect
• drug action
• chemical structure and
• molecular targets.

→ Proteins which perform the role of biological catalysts in the body are called enzymes.

→ Proteins that are crucial to body’s communication process are called receptors.

→ Drugs can block the binding site of the enzyme and prevent binding of substrate or can inhibit the catalytic activity of the enzyme. Such drugs are called enzyme inhibitors.

→ In the body message between two neurons and that between neurons to muscles is communicated through certain chemicals known as chemical messengers.

→ Drugs that bind to the receptor site and inhibit its natural function are called antagonists.

→ Drugs that mimic the natural messenger by switching on the receptor are called agonists.

→ Antacids are used to counteract the effects of excess acid in the stomach.

→ A chemical, histamine, stimulates the secretion of pepsin and hydrochloric acid in the stomach.

→ Cimetidine (Tegamet) and ranitidine (Zantac) are used as antacids.

→ Histamine is a potent vasodilator. It is responsible for the nasal congestion associated with common cold and allergic response to pollen.

→ Bromphenaramine (Dimetapp) and terfenadine (Seldane) act as antihistamines.

→ Tranquilizers and analgesics are neurologically active drugs.

→ Tranquilizers are a class of chemical com-pounds used for the treatment of stress and mild or even severe mental diseases.

→ Iproniazid and phenelzine are antidepressant drugs.

→ Chlordiazepoxide and meprobamate are relatively mild tranquilizers suitable for relieving tension.

→ Equanii is used in controlling depression and hypertension.

→ Barbiturates are hipnotic, i.e., sleep produc-ing agents.

→ Analgesics reduce or abolish pain without causing disturbances of nervous system.

→ Aspirin and paracetamol are non – narcotic analgesics.

→ Drugs which reduce fever are called anti-pyretics.

→ Morphine narcotics are chiefly used for the relief of post operative pain, cardiac pain etc.

→ An antimicrobial drug tends to destroy / prevent development or inhibit pathogenic action of microbes such as bacteria, fungi, virus and other parasites selectively.

→ Salvarsan was discovered by Paul Ehrlich. It was used for the treatment of syphilis.

→ Penicillin was discovered by Alexander Fleming.

→ Ampicillin, Amoxycillin, Chloramphenicol are examples for broad spectrum antibiotics.

→ Penicillin G has a narrow spectrum.

→ Antiseptics and disinfectants are chemicals which either kill or prevent the growth of micro organisms.

→ Antiseptics are applied to living tissues such as wounds, cuts, ulcers and diseased skin surfaces.

→ Dettol is a mixture of chloroxylenol and terpineol.

→ Boric acid in dilute aqueous solution is a weak antiseptic for eyes.

→ Disinfectants are applied to inanimate objects such as floors, drainage system, instruments etc.

→ Antifertility drugs are used to check population explosion.

→ Birth control pills essentially contain a mixture of synthetic estrogen and progesterone derivatives.

→ Norethindrone is an example of synthetic progesterone derivative most widely used as antifertility drug.

→ The estrogen derivative which is used in combination with progesterone derivative is ethynylestradiol (novestrol).

→ Artificial sweeteners are preferred by diabetic persons and people who need to control intake of calories.

→ Saccharin, Aspartame, Sucralose, Alitame, etc. are examples for artificial sweeteners.

→ Food preservatives prevent spoilage of food due to microbial growth.

→ Sodium benzoate is an important food preservative.

→ Salts of sorbic acid and propanoic acid are also used as food preservatives.

→ Anti oxidants help in food preservation by retarding the action of oxygen on food.

→ Butylated hydroxy toluene (BHT) and Butylated hydroxy anisole (BHA) are the most familiar antioxidants. Sometimes these are used along with citric acid for more effective action.

→ Soaps and detergents are used as cleansing agents.

→ Soaps used for cleaning purpose are sodium or potassium salts of long chain fatty acids, e.g., stearic, oleic and palmitic acids.

→ Sodium or potassium soaps do not work in hard water. Synthetic detergents can be used both in soft and hard water.

→ Branched chain detergents are not easily degraded by bacteria easily. Slow degradation of detergents leads to their accumulation and cause environmental pollution.

→ Unbranched hydrocarbon detergents are biodegradable.

Students can go through TS Inter 2nd Year Chemistry Notes 9th Lesson Biomolecules will help students in revising the entire concepts quickly.

TS Inter 2nd Year Chemistry Notes 9th Lesson Biomolecules

→ Carbohydrates are optically active polyhydroxy aldehydes or ketones or molecules which provide such units on hydrolysis.

→ Most of the carbohydrates have the general formula C_x(H₂O)_y.

→ Carbohydrates which are sweet to taste are called sugars.

→ Carbohydrates are also called saccharides.

→ On the basis of hydrolysis, carbohydrates are classified into monosaccharides, oligosaccharides and polysaccharides.

→ Carbohydrates which cannot be hydrolysed into simpler units are called monosaccharides. Ex: Glucose, fructose.

→ Carbohydrates which yield two to ten mono-saccharide units on hydrolysis are called oligosaccharides.

→ Sucrose (Cane sugar) is a disaccharide. It gives one molecule of glucose and one molecule of fructose on hydrolysis.

→ Maltose on hydrolysis gives two molecules of glucose only.

→ Carbohydrates which yield a large number of monosaccharide units on hydrolysis are called polysaccharides. Ex: Starch, cellulose.

→ Glucose is an aldohexose whereas fructose is a ketohexose. Glucose is also known as dextrose.

→ In the laboratory glucose is prepared by boiling sucrose with dil. HCl or H₂SO₄ in alcoholic solution.

→ Starch on boiling with dilute H₂SO₄ at 120°C and under pressure, undergoes hydrolysis and gives Glucose.

→ On prolonged heating with HI glucose forms n – Hexane.

→ Glucose reacts with hydroxylamine to give an oxime.

→ Glucose is oxidised by bromine water to give gluconic acid.

→ Acetylation of glucose with acetic anhydride gives glucose pentaacetate.

→ Glucose and gluconic acid on oxidation with nitric acid give saccharic acid.

→ The letter ‘D’ or ‘L’ before the name of any compound indicates relative configuration of a particular stereo isomer.

→ Glucose is correctly named as D – (+) – glucose. Here (+) represents dextrorotatory nature.

→ The open chain structure of glucose explained most of its properties but it could not explain some facts regarding glucose. Glucose does not give Schiff’s test and it does not form bisulphite addition product with NaHSO₃.

→ A pyranose ring structure was proposed for glucose.

→ Glucose exists in two cyclic hemiacetal forms which differ in their configuration at C₁, called the anomeric carbon. These isomers
i. e., α – form and β – form are called anomers.

→ Glucose is dextrorotatory whereas fructose is laevorotatory.

→ Fructose is given a furanose ring structure.

→ The two monosaccharide units in a disaccharide are joined by an oxide linkage formed by the loss of a water molecule. Such a linkage between two monosaccharide units through oxygen atom is called glycosidic linkage.

→ Sucrose on hydrolysis gives equimolar mixture of glucose and fructose. The product is called invert sugar.

→ Lactose on hydrolysis gives galactose and glucose.

→ Starch is a polymer of a – glucose and consists of two components – Amylose and Amylopectin.

→ The carbohydrates are stored in animal body as glycogen.

→ Proteins are the polymers of about 20 different α – amino acids which are linked by peptide bonds.

→ Amino acids which can be synthesised in the body are called non – essential amino acids. Ex: Glycine, Alanine.

→ Amino acids which cannot be synthesised in the body and must be obtained through diet are known as essential amino acids. Ex: Valine, Lysine.

→ When a protein in its native form, is subjected to physical change like change of temperature or chemical change like change in pH, it loses its biological activity. This is called denaturation of protein.

→ Enzymes are biocatalysts which speed up the reactions in biosystems.

→ Vitamins are organic molecules which are required in small quantities in our diet and their deficiency causes specific diseases.

→ Nucleic acids are five membered ring sugars linked by phosphate groups.

→ Nucleic acids are mainly of two types.

• Deoxyribonucleic acid (DNA) and
• Ribo-nucleic acid (RNA). Nucleic acids are also called polynucleotides.

→ Hormones are molecules that act as intercellular messengers.

→ Hormones have several functions in the body and help to maintain the balance of biological activities in the body.