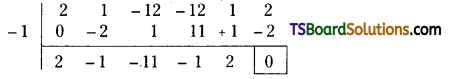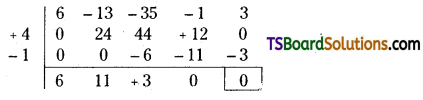Mahesh

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 6 Integration will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Integration Formulas

→ A function F(x) Is called an anti derivative or indefinite Integral of a function f(x) If \(\frac{d}{d x}\)[F (x)] = f(x).

→ Indefinite Integrals:
Let f(x) be a function. Then the collection of all its anti derivatives is called the indefinite integral of f(x) and it is denoted by ∫f(x) dx.
Thus \(\frac{d}{d x}\) [F(x) + c] = f(x) ⇔ ∫f(x)dx = F(x) + c
where F(x) is the anti derivative and c is the arbitrary constant known as the constant of integration.

→ Standard forms:
∫K dx = Kx + c, K is constant

→ ∫1 dx = x + c

→ ∫xⁿ dx = \(\frac{x^{n+1}}{n+1}\) + c, n ≠ -1

→ ∫x dx = \(\frac{x^2}{2}\) + c

→ ∫√x dx = \(\frac{2}{3}\)x√x + c

→ ∫\(\frac{1}{\sqrt{x}}\)dx = 2√x + c

→ ∫\(\frac{1}{x^2}\)dx = \(\frac{-1}{x}\) + c

→ ∫\(\frac{1}{x}\)dx = log |x| + c

→ ∫e^xdx = e^x + c

→ ∫a^xdx = \(\frac{a^x}{\log a}\) + c

→ ∫sin x dx = – cos x + c

→ ∫cos x dx = sin x + c

→ ∫tan x dx = log|sec x| + c = -log |cos x| + c

→ ∫cot x dx = log|sin x| + c = -log|cosec x| + c

→ ∫sec x dx = log|sec x + tan x| + c = log|tan\(\left(\frac{\pi}{4}+\frac{x}{2}\right)\)| + c

→ ∫cosec x dx = log|cosec x – cot x| + c = log|tan\(\frac{x}{2}\)| + c

→ ∫sec²x dx = tan x + c

→ ∫cosec²x dx = -cot x + c

→ ∫sec x tan x dx = sec x + c

→ ∫cosec x cot x dx = -cosec x + c

→ ∫sin hx dx = cos hx + c

→ ∫cos hx dx = sin hx + c

→ ∫tan hx dx = log|cos hx| + c

→ ∫cot hx dx = log |sin hx| + c

→ ∫sech²x dx = tan hx + c

→ ∫cosech²x dx = -cot hx + c

→ ∫sec hx tan hx dx = -sec hx + c

→ ∫cosec hx cot hx dx = – cosec hx + c

→ ∫\(\frac{1}{\sqrt{1-x^2}}\) dx = sin^-1x + c

→ ∫\(\frac{1}{\sqrt{x^2-1}}\) dx = cosh^-1x + c = log(x + \(\sqrt{x^2-1}\)) + c

→ ∫\(\frac{1}{\sqrt{x^2+1}}\) dx = sin h^-1x + c = log(x + \(\sqrt{x^2+1}\)) + c

→ ∫\(\frac{1}{1+x^2}\)dx = tan^-1 x + c

→ ∫\(\frac{1}{1-x^2}\)dx = \(\frac{1}{2}\)log\(\left|\frac{1+x}{1-x}\right|\) + c

→ ∫\(\frac{1}{x^2-1}\)dx = \(\frac{1}{2}\)log\(\left|\frac{x-1}{x+1}\right|\) + c

→ ∫\(\frac{1}{x \sqrt{x^2-1}}\)dx = sec^-1x + c

→ ∫\(\frac{1}{\sqrt{a^2-x^2}}\)dx = sin^-1\(\left(\frac{x}{a}\right)\) + c

→ \(\frac{1}{a^2+x^2}\)dx = \(\frac{1}{a}\)tan^-1\(\left(\frac{x}{a}\right)\) + c = \(\frac{-1}{a}\)cot^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\frac{1}{\sqrt{a^2+x^2}}\)dx = sinh^-1\(\left(\frac{x}{a}\right)\) + c = log(x + \(\sqrt{a^2+x^2}\)) + c

→ ∫\(\frac{1}{\sqrt{x^2-a^2}}\)dx = cosh^-1\(\left(\frac{x}{a}\right)\) + c = log(x + \(\sqrt{x^2-a^2}\)) + c

→ ∫\(\frac{1}{a^2-x^2}\)dx = \(\frac{1}{2 a}\)log \(\left|\frac{a+x}{a-x}\right|\) + c

→ ∫\(\frac{1}{x^2-a^2}\)dx = \(\frac{1}{2 a}\)log \(\left|\frac{x-a}{x+a}\right|\) + c

→ ∫\(\sqrt{a^2-x^2}\)dx = \(\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2}\)sin^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\sqrt{a^2+x^2}\)dx = \(\frac{x}{2} \sqrt{a^2+x^2}+\frac{a^2}{2}\)sinh^-1\(\left(\frac{x}{a}\right)\) + c

→ ∫\(\sqrt{x^2-a^2}\)dx = \(\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2}\)cosh^-1\(\left(\frac{x}{a}\right)\) + c

→ \(\frac{d}{d x}\)[∫f(x)dx] = f(x)

→ ∫kf(x) dx = k.∫f(x)dx

→ ∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g(x)dx

→ ∫\(\frac{f^{\prime}(x)}{f(x)}\)dx = log|f(x)| + c

→ ∫\(\frac{f^{\prime}(x)}{\sqrt{f(x)}}\)dx = 2\(\sqrt{f(x)}\) + c

→ ∫[f(x)]ⁿ.f'(x)dx = \(\frac{f^{n+1}(x)}{n+1}\) + c, n ≠ -1

→ ∫\(\frac{f^{\prime}(x)}{1+[f(x)]^2}\)dx = tan^-1f(x) + c

→ Evaluation of Integral of various types by using standard results:

→ IntegratIon by parts: If U and V are two functions of x, then
∫UV dx = U∫V dx – ∫[\(\frac{dU}{d x}\)∫Vdx]dx

Extension Rule: ∫UVdx = UV₁ – U’V₂ + U”V₃ – U”’V₄ + ……….. + U where U’, U”, U”’ etc., are the successive derivatives of U and V₁, V₂, V₃ etc., are successive integrals of V.
Note : This rule is very useful if one of the Integrand Is an algebraic function.

→ Formulae:

• ∫e^ax sinbx dx = \(\frac{e^{a x}}{a^2+b^2}\)[a sin bx – b cos bx] + c
• ∫e^ax cos bx dx = \(\frac{e^{a x}}{a^2+b^2}\)[a cos bx – b sin bx] + c
• ∫e^x[f(x) + f'(x)]dx = e^xf(x) + c
• ∫e^-x[f(x) + f'(x)]dx = -e^-xf(x) + c
• ∫e^ax[af(x) + f'(x)]dx = e^axf(x) + c

→ Reduction Formulae:

• If I_n = ∫xⁿe^ax dx then I_n = \(\frac{x^n e^{a x}}{a}-\frac{n}{a}\)I_n-1
• If I_n = ∫sinⁿx dx then I_n = \(\frac{-\sin ^{n-1} x \cos x}{n}+\frac{n-1}{n}\)I_n-2
• If I_n = ∫cosⁿxdx then I_n = \(\frac{\cos ^{n-1} x \sin x}{n}+\frac{n-1}{n}\)I_n-2
• If I_n = ∫tanⁿx dx then I_n = \(\frac{\tan ^{n-1} x}{n-1}\) – I_n-2
• If I_n = ∫cotⁿx dx then I_n = \(\frac{-\cot ^{n-1} x}{n-1}\)I_n-2
• If I_n = ∫secⁿx dx then I_n = \(\frac{\sec ^{n-2} x \tan x}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = ∫cosecⁿx dx then I_n = \(\frac{-{cosec}^{n-2} x \cot x}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = ∫(log x)ⁿ dx then I_n = x(log x)ⁿ – nI_n-1

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Theory of Equations Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Theory of Equations Important Questions Long Answer Type

Question 1.
If the roots of the equation x³ + 3px² + 3qx + r = 0 are in AP then show that 2p³ – 3pq + r = 0. [May ’08]
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
Since the roots are in A.P then they must be of the form a – d, a, a + d.
Now, s₁ = a – d + a + a + d = \(\frac{-3 p}{1}\)
3a = – 3p
a = – p
Since a is a root of x³ + 3px² + 3qx + r = 0 then
(- p)³ + 3p (- p)² + 3q(- p) + r = 0
⇒ – p³ + 3p³ – 3pq + r = 0
⇒ 2p³ – 3pq + r = 0.

Question 2.
If the roots of the equation x³ + 3px² + 3qx + r = 0 are in G.P then show that p³r = q³. [March ‘03]
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
Since the roots are in G.P then they must be of the form \(\frac{a}{r}\), a, ar
Now, s₃ = \(\frac{a}{r}\) . a . ar
= \(\frac{-\mathrm{r}}{1}\) = – r
⇒ a³ = – r
⇒ a = (- r)^1/3
Since a is a root of x³ + 3px² + 3qx + r = 0 then
\(\left((-r)^{1 / 3}\right)^3+3 p\left((-r)^{1 / 3}\right)^2+3 q\left((-r)^{1 / 3}\right)\) + r = 0
⇒ – r + 3p (- r)^2/3 + 3q(- r)^1/3 + r = 0
⇒ 3p(- r)^2/3 = – 3q(- r)^1/3
Cubing on both sides,
⇒ p³ (- r)² = – q³(- r)
⇒ p³ r² = q³r
⇒ p³r = q³

Question 3.
If the roots of the equation x³ + 3px² + 3q + r = 0 are in H.P then show that 2q³ = r (3pq – r).
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
The roots of x³ + 3px² + 3qx + r = 0 are in H.P.
The roots of \(\left(\frac{1}{x}\right)^3+3 p\left(\frac{1}{x}\right)^2+3 q\left(\frac{1}{x}\right)\) + r = 0 are in A.p.
\(\frac{1}{x^3}+\frac{3 p}{x^2}+\frac{3 q}{x}\) + r = 0 are in A.P
⇒ 1 + 3px + 3qx² + rx³ = o
⇒ rx³ + 3qx² + 3px + 1 = 0 ……………..(1)
Let the roots of (1) be a – d, a, a + d
s₁ = a – d + a + a + d = \(\frac{-3 q}{r}\)
⇒ 3a = \(\frac{-3 q}{r}\)
a = \(\frac{-q}{r}\)
Since a is a root of (1)
⇒ \(r \cdot \frac{-q^3}{r^3}+3 q \cdot \frac{q^2}{r^2}+3 p \cdot \frac{-q}{r}+1\) = 0
⇒ \(\frac{-q^3}{r^2}+\frac{3 q^3}{r^2}-\frac{3 p q}{r}\) + 1 = 0
⇒ 2q³ = r (3pq – r). +
Hence proved.

Question 4.
Solve 4x³ – 24x² + 23x + 18 = 0, given that the roots of this equation are in arithmetic
progression. [Mar. ’14, May ’06, ’01]
Solution:
Given equation is 4x³ – 24x² + 23x + 18 = 0
Given that the roots of this equation are in A.P.
Since the roots are in A.P, they must be of the form, a – d, a, a + d.
Now, a – d + a + a + d = \(-\frac{-24}{4}\) = 6
⇒ 3a = 6
⇒ a = 2
(a – d) a (a + d) = \(\frac{-18}{4}\)
(a² – d²)a = \(\frac{-9}{2}\)
(4 – d²)2 = \(\frac{-9}{2}\)
4 – d² = \(\frac{-9}{4}\)
d² = 4 + \(\frac{9}{4}\) = \(\frac{25}{4}\)
d = ± \(\frac{5}{2}\)

Case – I:
If a = 2, d = \(\frac{5}{2}\)
The roots of given equation are – \(\frac{-1}{2}\), 2, \(\frac{9}{2}\).

Case-2:
If a = 2, d = \(\frac{-5}{2}\)
The roots of given equation are \(\frac{9}{2}\), 2, \(\frac{-1}{2}\).

Question 5.
Solve x³ – 3x² – 6x + 8 = 0, given that the : roots are in A.P. [March ’07]
Solution:
Given equation is x³ – 3x² – 6x + 8 = 0
Since, the roots are in A.P., thus they must; be of the form a – d, a, a + d.
Now, a – d + a + a + d = \(\frac{-(-3)}{1}\) = 3
⇒ 3a = 3
⇒ a = 1
⇒ (a – d) a (a + d) = \(\frac{-8}{1}\)
a² – d² = – 8
1 – d² = – 8
d = 9
⇒ d = ±3
Case – 1 : If d = 3; a = 1
The roots of the given equation are; a – d, a, a + d = – 2, 1, 4.

Case – 2: If d = – 3; – a = 1;
The roots of the given equation are (a – d) a, (a + d) = 4, 1, – 2 .

Question 6.
Solve x³ – 7x² + 14x – 8 = 0, given that the roots are in geometric progression. [May ’07]
Solution:
Given equation is x³ – 7x² + 14x – 8 = 0
Given that the roots are in G.P then they may be of the form \(\frac{a}{r}\), a, ar
\(\frac{a}{r}\) + a + ar = a [\(\frac{1}{r}\) + 1 + r] = \(\frac{-(-7)}{1}\)
⇒ a[\(\frac{1}{r}\) + 1 + r] = 7 …………..(1)
\(\frac{a}{r}\) . a . ar = 1
⇒ a³ = 8
⇒ a = 2
(1) ⇒ 2\(\left(\frac{r^2+r+1}{r}\right)\) = 7
⇒ 2r² – 5r + 2 = 0
⇒ 2r² – 4r – r + 2 = 0
⇒ 2r (r – 2) – 1 (r – 2) = 0
⇒ (2r – 1) (r – 2) = 0
⇒ r = \(\frac{1}{2}\) (or) r = 2
Case – 1:
If a = 2, r = \(\frac{1}{2}\)
The roots of given equation are \(\frac{a}{r}\), a, ar = 4, 2, 1
Case – 2 :
If a = 2, r = 2
The roots of given equation are \(\frac{a}{r}\), a, ar = 1, 2, 4.

Question 7.
Solve the equation 15x³ – 23x² + 9x – 1 = 0, the roots being in H.P. [May ’02]
Solution:
Giveti equation is 15x³ – 23x² + 9x – 1 = 0
The roots of 15x³ – 23x² + 9x – 1 = 0 are in H.P
The roots of
\(15 \cdot \frac{1}{x^3}-23 \cdot \frac{1}{x^2}+9 \cdot \frac{1}{x}-1\) = 0 are in A.P.
15 – 23x + 9x² – x³ = 0
⇒ x³ – 9x² + 23x – 15 = 0
Let the roots be a – d, a, a + d
a – d + a + a + d = \(\frac{-(-9)}{1}\) = 9
⇒ 3a = 9
⇒ a = 3
(a – d) a (a + d) = \(\frac{-(-15)}{1}\) = 15
⇒ a(a² – d²) = 15
⇒ 3(9 – d²) = 15
9 – d² = 5
d² = 4
d = 21
The roots of x³ – 9x² + 23x – 15 = 0 are a – d, a, a + d =3 – 2, 3, 3 + 2 = 1, 3, 5
The roots of 15x³ – 23x² + 9x – 1 = 0 are \(\frac{1}{1}, \frac{1}{3}, \frac{1}{5}\) = 1, \(\frac{1}{3}, \frac{1}{5}\).

Question 8.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots. [May ’11, March ‘05] [AP – Mar.2019]
Solution:
Given that one root is equal to half of the sum of the remaining roots.
Given equation is 18x³ + 81x² + 121x + 60 = 0
i.e., the roots are in A.P.
Let a – d, a, a + d be the roots of the given equation.
∴ a – d + a + a + d = \(\frac{-81}{18}\)
3a = \(\frac{-81}{18}\)
a = \(\frac{-3}{2}\)
(a – d) a (a + d) = \(\frac{-60}{18}\)
a(a – d) = \(\frac{-81}{18}\)
\(\frac{-3}{2}\left(\frac{9}{4}-d^2\right)=\frac{-60}{18}\)
d² = \(\frac{9}{4}-\frac{20}{9}=\frac{81-80}{36}=\frac{1}{36}\)
d = \(\frac{1}{6}\)
∴ The roots of the given equation are a – d, a, a + d = \(\frac{-3}{2}-\frac{1}{6}, \frac{-3}{2}, \frac{-3}{2}+\frac{1}{6}\)
= \(\frac{-5}{3}, \frac{-3}{2}, \frac{-4}{3}\)

Question 9.
Given that one root of 2x³ + 3x² – 8x + 3 = 0 is double the other root, find the roots of the equation. [May ’03]
Solution:
Given equation is 2x³ + 3x² – 8x + 3 = 0
Now, α + β + γ = \(\frac{-3}{2}\) …………..(1)
αβ + βγ + γα = \(\frac{-8}{2}\) = – 4 ……………(2)
αβγ = \(\frac{-3}{2}\) ……………..(3)
Given one root is double the other then
α = 2β
(1) ⇒ 2β + β + γ = \(\frac{-3}{2}\)
⇒ 3β + γ = \(\frac{-3}{2}\)
⇒ γ = \(\frac{-3}{2}\) – 3β …………….(4)
(2) ⇒ 2β . β + βγ + γ . 2β = – 4
2β² + βγ + 2βγ = – 4
2β² + 3βγ = – 4 ……………..(5)
From (4) & (5)
2β² + 3β(\(\frac{-3}{2}\) – 3β) = – 4
2β² – \(\frac{9 \beta}{2}\) – 9β²=
⇒ \(\frac{4 \beta^2-9 \beta-18 \beta^2}{2}\) = – 4
⇒ – 14β² – 9β = – 8
⇒ 14β² + 9β – 8 = 0
⇒ 14β² + 16β – 7β – 8 = 0
⇒ (2β – 1) (7β + 8) = 0
⇒ β = \(\frac{-8}{7}\) (or) β = \(\frac{1}{2}\)
β = \(\frac{-8}{7}\) does not satisfy the given equation.
β = \(\frac{1}{2}\)
⇒ α = 2 . \(\frac{1}{2}\) = 1
Substitute the value of β in equation (4)
⇒ γ = \(\frac{-3}{2}\) – 3 . \(\frac{1}{2}\)
= \(\frac{-3-3}{2}=\frac{-6}{2}\) = – 3.
∴ The roots of the given equation are 1, \(\frac{1}{2}\), – 3.

Question 10.
Solve x⁴ + x³ – 16x² – 4x + 48 = 0, given that the product of two of the roots is 6. [TS – Mar. 2019; May ’12. ’09]
Solution:
Given equation is x⁴ + x³ – 16x² – 4x + 48 = 0
Let α, β, γ, δ are the roots of the given equation.
Then αβγδ = \(\frac{48}{1}\) = 48
Given that the product of the two roots of the given equation is 6.
Suppose that αβ = 6
Now, 6γδ = 48
γδ = 8
Let α + β = p, γ + δ = q
The quadratic equation whose roots are α, β is
x² – x(α + β) + αβ = 0
x² – px + 6 = 0 ………….(1)
The quadratic equation whose roots are γ, δ is
x² – x (γ + δ) + γδ = 0
⇒ x² – qx + 8 = 0 ……………(2)
∴ x⁴ + x³ – 16x² – 4x + 48
= (x² – px + 6) (x² – qx + 8)
= x⁴ – qx³ + 8x² – px³ + pqx² – 8px + 6x² – 6qx + 48
= x⁴ + (- p – q)x³ + (pq+ 14)x² + (- 8p – 6q) x + 48
Now comparing coefficients of x³ on both sides, we get
⇒ – p – q = 1
⇒ p + q = – 1 ………………(3)
Now comparing coefficients of x on both sides, we get
– 8p – 6q = – 4
⇒ 4p + 3q = 2 ……………….(4)
Solve (3) and (4);

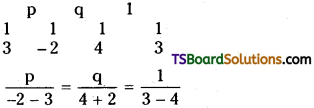
⇒ p = \(\frac{-5}{-1}\)
⇒ q = \(\frac{6}{-1}\)
⇒ p = 5, q = – 6
Substitute ‘p’ value in (1),
x² – 5x + 6 = 0
⇒ x² – 3x – 2x + 6 = 0
⇒ x (x – 3) – 2 (x – 3) = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, x = 3
Substitute ‘q’ value in (2),
(2) ⇒ x² + 6x + 8 = 0
⇒ x² + 4x . 2x + 8 = 0
⇒ (x + 2) (x +4) = 0
⇒ x = – 4, x = – 2
∴ The roots of given equation are 3, 2, – 4, – 2.

Question 11.
Given that two roots of 4×3+20×2-23x+6=O are equal, find all the roots of the given equation.
Solution:
Given equation is 4x³ + 20x² – 23x + 6 = 0
Let α, β, γ be the roots of given equation.
Then s₁ = α + β + γ = \(\frac{-(20)}{4}\)
⇒ α + β + γ = – 5 …………….(1)
⇒ αβ + βγ + γα = \(\frac{-23}{4}\) ……………(2)
⇒ αβγ = \(\frac{-6}{4}=\frac{-3}{2}\) ………….(3)
Given that two roots are equal
⇒ β = α
(1) ⇒ 2α + γ = – 5
⇒ γ = – 5 – 2α
(2) ⇒ α² + αy + αy = \(\frac{-23}{4}\)
⇒ α² + 2αγ = \(\frac{-23}{4}\)
⇒ α² + α (- 5 – 2α) = \(\frac{-23}{4}\)
⇒ 4 (α² – 10α – 4α²) = – 23
⇒ 4 (- 3α² – 10α) = – 23
⇒ 12α² + 40α – 23 = 0
⇒ 12α² + 46α – 6α – 23 = 0
⇒ 2α (6α + 23) – 1(6α + 23) = 0
⇒ (6α + 23) (2α – 1) = 0
∴ α = \(\frac{-23}{6}\) does not satisfy given equation.
∴ α = \(\frac{1}{2}\)
⇒ β = \(\frac{1}{2}\)
γ = – 5 – 2 . \(\frac{1}{2}\) = – 6
γ = – 6
∴ The roots of the given equation are \(\frac{1}{2}\), \(\frac{1}{2}\), – 6.

Question 12.
Solve x⁴ + 4x³ – 2x² – 12x + 9 = 0, given that it has two pairs of equal roots. [March ’11, ’03]
Solution:
Given equation is x⁴ + 4x³ – 2x² – 12x + 9 = 0
Given that it has two pairs of equal roots then let the roots of the given equation be
α + α + β + β = \(\frac{-4}{1}\)
⇒ 2 (α + β) = – 4
⇒ α + β = – 2
αα + αβ + βα + βα + αβ + β² = \(\frac{-2}{1}\)
α² + 4αβ + β²
(α + β)² + 2αβ = – 2
4 + 2αβ = – 2
2αβ = – 6
αβ = – 3
We know that,
(α – β)² = (α + β)² – 4αβ
= 4 – 4 (- 3)
= 4 + 12 = 16

α – β = 4
α + β = – 2
⇒ 2α = 2
⇒ α = 1

α + β = – 2
1 + β = – 2
β = – 3
∴ The roots of the given equation are 1, 1, – 3, – 3.

Question 13.
Find the roots of x⁴ – 16x³ + 86x² – 176x + 105 = 0. [March ’08, ’02]
Solution:
Let f(x) = x⁴ – 16x³ + 86x² – 176x + 105 = 0
If x = 1 then f(1)= 1 – 16 + 86 – 176 + 105 = 0
= 192 – 192 = 0
Hence, 1 is a root of f(x) = 0
If x = 3 then
f(3) = 81 – 16 (27) + 86(9) – 176(3) + 105
= 81 – 432+ 774 – 528 + 105
= 960 – 960 = 0
Hence 3 is a root of f(x) = 0.
By the method of synthetic division we have

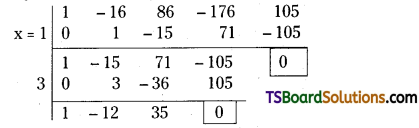
∴ The quotient is x² – 12x + 35 and remainder is zero.
∴ f(x) = x⁴ – 16x³ + 86x² – 176x + 105
= (x – 1)(x – 3) (x² – 12x + 35)
= (x – 1) (x – 3) (x – 5) (x – 7)
Hence the roots of the given equation are 1, 3, 5, 7.

Question 14.
Solve x⁴ – 10x³ + 26x² – 10x + 1 = 0. [TS – Mar. ‘18; Mar. ‘12, ’10, Board Paper]
Solution:
Given equation is x – 10x³ + 26x² – 10x + 1 = O
This is standard form of reciprocal equation.
The given equation is a reciprocal degree of class – 1 on dividing with x²
⇒ x² – 10x + 26 – \(\frac{10}{x}+\frac{1}{x^2}\) = 0
\(\left(x^2+\frac{1}{x^2}\right)-10\left(x+\frac{1}{x}\right)\) + 26 = 0
If x + \(\frac{1}{x}\) = a
⇒ x² + \(\frac{1}{x^2}\) = a² – 2
⇒ (a² – 2) – 10a + 26 = 0
⇒ a² – 10a + 24 = 0
⇒ a² – 6a – 4a + 24 = 0
⇒ a (a – 6) – 4 (a – 6) = 0
If (a – 4) (a – 6) = 0
⇒ a = 4, a = 6
If a = 4
⇒ x + \(\frac{1}{x}\) = 4
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{-(-4) \pm \sqrt{16-4(1)}}{2(1)}\)
= \(\frac{4 \pm \sqrt{12}}{2}\)
= 2 ± √3
If a = 6 x + \(\frac{1}{x}\) = 4
⇒ x² – 6x + 1 = 0
x = \(\frac{-(-6) \pm \sqrt{36-4(1)(1)}}{2(1)}=\frac{6 \pm \sqrt{32}}{2}\)
= 3 ± 2√2
Hence ti roots of the given equation are 2 ± √3, 3 ± 2√2.

Question 15.
Solve the quation 6x⁴ – 35x³ + 62x² – 35x + 6 = 0. [May ’13, ’10]
Solution:
Given equation is 6x⁴ – 35x³ + 62x² – 35x + 6 = 0
This is a standard form of reciprocal equation.
The given equation is an even degree reciprocal equation of class – 1
On dividing both sides of given equation by x², we get
6x² – 35x + 62 – \(\frac{35}{x}+\frac{6}{x^2}\) = 0
\(6\left(x^2+\frac{1}{x^2}\right)-35\left(x+\frac{1}{x}\right)\) + 62 = 0
Let x + \(\frac{1}{x}\) = a
⇒ \(\mathrm{x}^2+\frac{1}{\mathrm{x}^2}\) = a² – 2
⇒ 6(a² – 2) – 35a + 62 = 0
⇒ 6a² – 12 – 35a + 62 = 0
⇒ 6a² – 35a + 50 = 0
⇒ 6a² – 15a – 20a + 50 = 0
⇒ 3a (2a – 5) – 10 (2a – 5) = 0
⇒ (2a – 5)(3a – 10) = 0
⇒ 2a = 5; 3a = 10
a = \(\frac{5}{2}\) a = \(\frac{10}{3}\)
If a = \(\frac{5}{2}\)
⇒ x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0
⇒ 2x² – 4x – x + 2 = 0
⇒ 2x (x – 2) – 1 (x – 2) = 0
⇒ x = \(\frac{1}{2}\) (or) x = 2
If a = \(\frac{10}{3}\)
⇒ x + \(\frac{1}{x}\) = \(\frac{10}{3}\)
⇒ 3x² + 3 = 10x
⇒ 3x² – 10x + 3 = 0
⇒ 3x² – 9x – x + 3 = 0
⇒ 3x (x – 3) – 1 (x – 3) = 0
x = \(\frac{1}{3}\) (or) x = 3
∴ The roots are 2, 3, \(\frac{1}{2}\), \(\frac{1}{3}\).

Question 16.
Solve 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0. [TS – May ‘15: AP-Mar. ’17, ‘16; March ‘08, ‘07]
Solution:
Given equation is 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
Let f(x) = 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0
If x = – 1
⇒ (- 1) = 2 (- 1) + 1 – 12 (- 1) – 12(1) + (- 1) + 2
= – 2 + 1 + 12 – 12 – 1 + 2 = 0
∴ (x + 1) is a factor of f(x).
On dividing f(x) by (x + 1) we get,

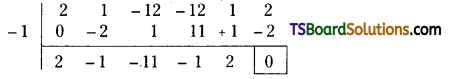
∴ 2x⁴ – x³ – 11x² – x + 2 = 0
On dividing with x² on both sides, we get
⇒ 2x² – x – 11 – \(\frac{1}{x}+\frac{2}{x^2}\) = 0
⇒ \(2\left(x^2+\frac{1}{x^2}\right)-1\left(x+\frac{1}{x}\right)\) – 11 = 0
Let x + \(\frac{1}{x}\) = a
⇒ x² + \(\frac{1}{x^2}\) + 2 = a²
⇒ x² + \(\frac{1}{x^2}\) = a² – 2
⇒ 2(a² – 2) – 1 (a) – 11 = 0
⇒ 2a² – 4 – a – 11 = 0
⇒ 2a² – a – 15 = 0
⇒ 2a² – 6a + 5a – 15 = 0
⇒ 2a (a – 3) + 5 (a – 3) = 0
⇒ (a – 3) (2a + 5) = 0
a = 3; a = – \(\frac{5}{2}\)
If a = 3;
x + \(\frac{1}{x}\) = 3
x² – 3x + 1 = 0
x = \(\frac{-(-3) \pm \sqrt{9-4}}{2(1)}=\frac{3 \pm \sqrt{5}}{2}\)
If a = – \(\frac{5}{2}\)
x + \(\frac{1}{x}\) = – \(\frac{5}{2}\)
⇒ 2x² + 5x + 2 = 0
⇒ 2x² + 4x + x + 2 = 0
⇒ 2x (x + 2) + 1 (x + 2) = 0
⇒ (2x + 1) (x + 2) = 0
∴ x = – \(\frac{1}{2}\), x = – 2
∴ The roots are – 1, – \(\frac{1}{2}\), – 2, \(\frac{3 \pm \sqrt{5}}{2}\).

Question 17.
Solve the equation x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0. [AP – May 2016; March ‘13]
Solution:
Given equation is x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1 = 0
Let f(x) = x⁵ – 5x⁴ + 9x³ – 9x² + 5x – 1
If x = 1
f(1)= 1⁵ – 5(1)⁴ + 9(1)³ – 9(1)² + 5(1) – 1
= 1 – 5 + 9 – 9 + 5 – 1 = 0
∴ (x – 1) is a factor of 1(x).
On dividing x⁵ – 5x³ + 9x³ – 9x² + 5x – 1 by x – 1

∴ x⁴ – 4x³ + 5x² – 4x + 1 = 0
This is a standard form of reciprocal equation.
Now, on dividing with x² on both sides, we get
x² – 4x + 5 – \(\frac{4}{x}+\frac{1}{x^2}\) = 0
\(\left(x^2+\frac{1}{x^2}\right)\) – 4 \(\left(x+\frac{1}{x}\right)\) + 5 = 0
Let x + \(\frac{1}{x}\) = a
⇒ [x + \(\frac{1}{x}\)]² = a²
⇒ x² + \(\frac{1}{x^2}\) + 2 = a²
⇒ x² + \(\frac{1}{x^2}\) = a² – 2
⇒ a² – 2 – 4a + 5 = 0
⇒ a² – 4a + 3 = 0
⇒ a² – 3a – a + 3 = 0
⇒ a (a – 3) – 1 (a – 3) = 0
⇒ (a – 1) (a – 3) = 0
⇒ a = 1 (or) a = 3
If a = 1
⇒ x + \(\frac{1}{x}\) = 1
⇒ x² – x + 1 = 0
⇒ x = \(\frac{-(-1) \pm \sqrt{1-4}}{2(1)}=\frac{1 \pm \mathrm{i} \sqrt{3}}{2}\)
If a = 3
⇒ x + \(\frac{1}{x}\) = 3
⇒ x² – 3x + 1 = 0
⇒ x = \(\frac{-(-3) \pm \sqrt{9-4}}{2(1)}=\frac{3 \pm \sqrt{5}}{2}\)
∴ The roots are 1, \(\frac{1 \pm \mathrm{i} \sqrt{3}}{2}\), \(\frac{3 \pm \sqrt{5}}{2}\).

Question 18.
Solve the equation 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0. [AP – Mar. ‘18. May 2015]
Solution:
Given equation is 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0
The given equation is an even degree reciprocal equation of class – 2.
Let f(x) = 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0
If x = 1 then f(1) = 6 – 25 + 31 – 31 + 25 – 6 = 0
∴ (x – 1) is a factor of f(x).
If x = – 1 then
f(- 1) = 6 + 25 + 31 – 31 – 25 – 6 = 0
∴ (x + 1) is a factor of f(x).
On dividing 1(x) by x + 1 and x – 1 we get,

∴ Quotient is 6x⁴ – 25x³ + 37x² – 25x + 6
6x⁴ – 25x³ + 37x² – 25x + 6 = 0
This is standard form of reciprocal equation.
This is an even degree reciprocal equation of class – 1.
On dividing both sides with x².
6x² – 25x + 37 – \(\frac{25}{x}+\frac{6}{x^2}\) = 0
\(6\left(x^2+\frac{1}{x^2}\right)-25\left(x+\frac{1}{x}\right)\) + 37 = 0
Let x + \(\frac{1}{x}\) = a
\(x^2+\frac{1}{x^2}\) = a² – 2
⇒ 6(a² – 2) – 25a + 37 = 0
⇒ 6a² – 25a + 25 = 0
⇒ 6a² – 15a – 10a + 25 = 0
⇒ 3a(2a – 5) – 5 (2a – 5) = 0
⇒ (3a -5) (2a – 5) = 0
⇒ a = \(\frac{5}{2}\), a = \(\frac{5}{3}\)
If a = \(\frac{5{2}\)
⇒ x + \(\frac{1}{x}\) = a
⇒ x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ 2x² – 5x + 2 = 0
⇒ 2x² – 4x – x + 2 = 0
⇒ 2x (x – 2) – 1 (x – 2) = 0
⇒ x = \(\frac{1}{2}\); x = 2
If a = \(\frac{5}{3}\)
⇒ x + \(\frac{1}{x}\) = \(\frac{5}{3}\)
⇒ 3x² – 5x + 3 = 0
x = \(\frac{-(-5) \pm \sqrt{25-4(3)(3)}}{2(3)}\)
= \(\frac{5 \pm \sqrt{25-36}}{6}=\frac{5 \pm \mathrm{i} \sqrt{11}}{6}\)
∴ The roots are ± 1, 2, \(\frac{1}{2}\), \(\frac{5 \pm \mathrm{i} \sqrt{11}}{6}\).

Question 19.
Find the polynomial equation of degree 5 whose roots are the translates of the roots of x₅ + 4x₃ – x₂ + 11 = 0 by – 3. [March ’06]
Solution:
Let f(x) = x⁵ + 4x³ – x² + 11 = 0
∴ The required equation is f(x + 3) = 0
∴ f(x + 3) = A₀x⁵ + A₁x⁴ + A₂x³ + A₃x² + A₄x + A₅
The coefficients A₀, A₁, A₂, A₃, A₄, A₅ can be obtained as follows

∴ Required equation is f(x + 3) = 0
x₅ + 15x₄ + 94x³ + 305x₂ + 507x + 353 = 0

Question 20.
Solve the equation x⁴ – 9x³ + 27x² – 29x + 6 = 0 given that one root is 2 – √3. [May ’03]
Solution:
Given equation is x⁴ – 9x³ + 27x² – 29x + 6 = 0
2 – √3 is a root of it then 2 + √3 is also root.
The quadratic factor of these two roots is (x – (2 + √3)) (x – (2 – √3))
= (x – (2 – √3)) (x – (2 + √3))
= ((x – 2) – √3) ((x – 2) + √3)
= (x – 2)² – (√3)²
= x² – 4x + 4 – 3
= x² – 4x + 1
On dividing x⁴ – 9x³ + 27x² – 29x + 6 with x² – 4x + 1

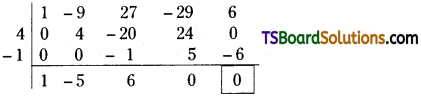
∴ Quotient is x² – 5x + 6 = 0
∴ x² – 5x + 6 = 0
⇒ x² – 3x – 2x + 6 = 0
⇒ x(x – 3) – 2 (x – 3) = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2 (or) x = 3
∴ The roots of given equation are 2, 3, 2 ± √3.

Question 21.
Show that x⁵ – 5x³ + 5x² – 1 = 0, has three equal roots and find that root. [TS – Mar. 2017]
Solution:
Given equation is x⁵ – 5x³ + 5x² – 1 = 0
Let f(x) = x⁵ – 5x³ + 5x² – 1
f'(x) = 5x⁴ – 15x² + 10x
f”(x) = 20x³ – 30x + 10
f(1) = 20 – 30 + 10 = 0
Similarly f'(1) = 0 and f(1) = 0
∴ (x – 1) is a factor of f”(x), f'(x) and f(x).
Thus f(x) = 0 has three equal roots and it is 1.

Question 22.
Find the condition that x³ – px² + qx – r = 0 may have the roots in G.P.
Solution:
q³ = p³r.

Question 23.
Solve 8x³ – 36x² – 18x + 81 = 0, given that the roots are in AP. [March ‘04]
Solution:
\(\frac{-3}{2}, \frac{3}{2}, \frac{9}{2}\).

Question 24.
Solve 3x³ – 26x² + 52x – 24 = 0, given that the roots are in A.P.
Solution:
\(\frac{2}{3}\), 2, 6

Question 25.
Solve the equation 6x³ – 11x² + 6x – 1 = 0, the roots being in H.P.
Solution:
1, \(\frac{1}{2}\), \(\frac{1}{3}\)

Question 26.
Solve x³ – 7x² + 36 = 0, gi0ven one root being twice the other.
Solution:
3, 6, – 2.

Question 27.
Solve x⁴ – 5x³ + 5x² + 5x – 6 = 0, given that the product of two of its roots ¡s 3.
Solution:
2, – 1, 3, 1

Question 28.
Solve 9x³ – 15x² + 7x – 1 = 0, given that two of its roots are equal.
Solution:
\(\frac{1}{3}\), \(\frac{1}{3}\), 1.

Question 29.
Solve x³ – 3x² – 10x + 48 = 0.
Solution:
3, – 4, 4.

Question 30.
Solve the equation 4x³ – 13x² – 13x + 4 = 0.
Solution:
– 1, \(\frac{1}{4}\), – 4

Question 31.
Find the polynomial equation whose roots are the translates of those of the equation. [TS – Mar. ’16]
x⁵ – 4x⁴ + 3x² – 4x + 6 = Oby – 3.
Solution:
x⁵ + 11x⁴ + 42x³ – 57x² – 13x – 60 = 0

Question 32.
Solve the equation x⁴ + 2x³ – 16x² – 22x + 7 = 0 given that 2 – √3 is one of its roots.
Solution:
2 ± √3, – 3 ± √2.

Some More Maths 2A Theory of Equations Important Questioons

Question 1.
Form the monic polynomial equation of degree 3 whose roots are 2, 3 and 6. [March ‘02]
Solution:
Let α = 2, β = 3, γ = 6
The monk equation having roots α, β, γ is
(x – α) (x – β) (x – γ) = 0
⇒ (x – 2) (x – 3) (x – 6) = 0
⇒ (x – 2) (x² – 9x + 18) =0
⇒ x³ – 9x² + 18x – 2x² + 18x – 36 = 0
⇒ x³ – 11x² + 36x – 36 = 0.

Question 2.
Form the monic polynomial equation of degree 4 whose roots are 4 + √3, 4 – √3, 2 + i and 2 – i.
Solution:
Let α = 4 + √3, β = 4 – √3, γ = 2 + i, δ = 2 – i
The equation whose roots are α, β, γ, δ is
(x – α) (x – β) (x – γ) (x – δ) = 0
(x – (4 + √3)) (x – (4 – √3))
(x – (2 + i)) (x – (2 – i)) = 0
((x – 4) – √3) ((x – 4) + √3)
((x – 2) – i) ((x – 2) + i) = 0
((x – 4)² – 3) ((x – 2)² – 2) = 0
(x² + 16 – 8x – 3) (x² + 4 – 4x + 1) = 0
(x² – 8x + 13) (x² – 4x + 5) = 0
x⁴ – 12x³ + 50x² – 92x + 65 = 0

Question 3.
Find s₁, s₂, s₃ and s₄ for the equation 8×4 – 2×3 – 27×2 – 6x + 9=0.
Solution:
Given equation is 8x⁴ – 2x³ – 27x² – 6x + 9 = 0
Comparing this equation with ax⁴ + bx³ + cx² + dx + e = 0
a = 8; b = – 2; c = – 27; d = – 6; e = 0
Now,
s₁ = \(\frac{-b}{a}=\frac{-(-2)}{8}=\frac{1}{4}\)
s₂ = \(\frac{c}{a}=\frac{-27}{8}\)
s₃ = \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-(-6)}{8}=\frac{3}{4}\)
s₄ = \(\frac{\mathrm{e}}{\mathrm{a}}=\frac{9}{8}\)

Question 4.
Find the algebraic equation whose roots are 3 times the roots of x³ + 2x² – 4x + 1 = 0.
Solution:
Let f(x) = x³ + 2x² – 4x + 1 = 0
∴ Required equation is f(\(\frac{x}{3}\)) = 0
\(\) = 0
⇒x3 + 6×2-36x + 27=0.

Question 5.
Find an algebraic equation of degree 4 whose roots are 3 times the roots of the equation 6x⁴ – 7x³ + 8x² – 7x + 2 = 0.
Solution:
Let f(x) = 6x⁴ – 7x³ + 8x² – 7x + 2 = 0
The required equation is f(\(\frac{x}{3}\)) = 0
\(\frac{6 x^4}{81}-\frac{7 x^3}{27}+\frac{8 x^2}{9}-\frac{7 x}{3}+2\) = 0
6x⁴ – 21x³ + 72x² – 189x + 162 = 0

Question 6.
Find the transfonned equation whose roots are the negatives of the roots of x⁴ + 5x³ + 11x + 3 = 0.
Solution:
Let f(x) = x⁴ + 5x³ + 11x + 3 = 0
Required equation ¡s f(- x) = 0
⇒ (- x)⁴ + 5(- x)³ + 11(- x) + 3 = 0
⇒ x⁴ – 5x³ – 11x + 3 = 0

Question 7.
Find the polynomial equation of degree 4 whose roots are the negatives of the roots of x⁴ – 6x³ + 7x² – 2x + 1 = 0.
Solution:
Let f(x) = x⁴ – 6x³ + 7x² – 2x + 1 = 0
The required equation is f(- x) = 0
⇒ (- x)⁴ – 6(- x)³ + 7(- x)² – 2(- x) + 1 = 0
⇒ x⁴ + 6x³ + 7x² + 2x + 1 = 0.

Question 8.
Find the polynomial equation whose roots are the reciprocals of the roots of x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0
Solution:
Let f(x) = x⁵ + 11x⁴ + x³ + 4x² – 13x + 6 = 0
The required equation is f(\(\frac{1}{x}\)) = o
⇒ \(\frac{1}{x^5}+\frac{11}{x^4}+\frac{1}{x^3}+\frac{4}{x^2}-\frac{13}{x}+6\) + 6 = 0
⇒ 1 + 11x + x² + 4x³ – 13x⁴ + 6x⁵ = 0
⇒ 6x⁵ – 13x⁴ + 4x³ + x² + 11x + 1 = 0

Question 9.
Find the polynomial equation whose roots are the reciprocals of the roots of the equation x⁴ + 3x³ – 6x² + 2x – 4 = 0.
Solution:
Let f(x) = x⁴ + 3x³ – 6x² + 2x – 4 = 0
The required equation is f(\(\frac{1}{x}\))) = 0
⇒ \(\frac{1}{x^4}+\frac{3}{x^3}-\frac{6}{x^2}+\frac{2}{x}-4\) = 0
⇒ 4x⁴ – 2x³ + 6x² – 3x – 1 = 0

Question 10.
Find the polynomial equation whose roots are the squares of the roots of x⁴ + x³ + 2x² + x + 1 = 0.
Solution:
Let f(x) = x⁴ + x³ + 2x² + x + 1 = 0
The required equation is f(√x) = 0
(√x)⁴ + (√x)³ + 2(√x)² + √x + 1 = 0
x² + x√x + 2x + √x + 1 = 0
x² + 2x + 1 = – x(√x) – √x
= – √x (x + 1)
⇒ squaring on both sides
(x² + 2x + 1)² = (- √x (x + 1))²
⇒ x⁴ + 4x² + 1 + 4x³ + 4x + 2x² = x(x² + 1 + 2x) = x³ + x + 2x²
x⁴ + 3x³ + 4x² + 3x + 1 = 0.

Question 11.
Find the polynomial equation whose roots are the squares of the roots of x³ – x² + 8x – 6 = 0.
Solution:
Let f(x) = x³ – x² + 8x – 6 = 0
∴ The required equation is f(√x) = o
(√x)³ – (√x)² + 8√x + 6 = 0
⇒ x√x – x + 8√x – 6 = 0
⇒ x + 6 = √x (x + 8)
⇒ squaring on both sides
⇒x² + 36 + 12x = x(x² + 64 + 16x)
⇒ x³ + 64x + 16x²
⇒ x³ + 15x² + 52x – 36 = 0.

Question 12.
Find the condition that x³ – px² + qx – r = 0 may have the roots in G.P.
Solution:
Given equation is x³ – px² + qx – r = 0
Since the roots are in G.P. then they must be the of the form \(\frac{a}{r}\), a, ar.
Now s₃ = \(\frac{a}{r}\) . a . ar
= \(\frac{-(-r)}{1}\)
a³ = r
a = r^1/3
Since ‘a’ is a root of x³ – px² + qx – r = 0
(r^1/3)³ – p(r^1/3)² + q(r^1/3) . r = 0.
⇒ r – pr^2/3 + qr^1/3 – r = 0
⇒ pr^2/3 = qr^1/3
Cubing on both sides.
⇒ p³r² = q³r
⇒ p³r = q³

Question 13.
Solve 8x³ – 36x² – 18x + 81 = 0, given that the roots are in AP.
Solution;
Given equation is 8x³ – 36x² – 18x + 81 = 0
Since, the roots are in A.P, they must be of the form a – d, a, a + d.
Now, a – d + a + a + d = \(\frac{-(-36)}{8}\)
⇒ 3a = \(\frac{9}{2}\)
⇒ a = \(\frac{3}{2}\)
(a – d) a (a + d) = \(\frac{-81}{8}\)
(a² – d²) a = \(\frac{-81}{8}\)
\(\frac{3}{2}\left(\frac{9}{4}-\mathrm{d}^2\right)=\frac{-81}{8}\)
\(\frac{9}{4}-d^2=\frac{-27}{4}\)
d² = 36
⇒ d = ± 3.

Case – I:
a = \(\frac{3}{2}\), d = 3
The roots of the given equation are a – d, a, a + d
\(\frac{-3}{2}, \frac{3}{2}, \frac{9}{2}\)

Case – II: a = \(\frac{3}{2}\), d = – 3
The roots of the given equation are a – d, a, a + d
\(\frac{9}{2}, \frac{3}{2}, \frac{-3}{2}\)

Question 14.
Solve 3x³ – 26x² + 52x – 24 = 0 the given, the roots are in Geometric Progression.
Solution:
Given equation is 3x³ – 26x² + 52x – 24 = 0
Since the roots are in G.P they must be of the form \(\frac{a}{r}\), a, ar.
Now, \(\frac{a}{r}\) + a + ar = \(\frac{-(-26)}{3}\)
a(\(\frac{1}{r}\) + 1 + r) = \(\frac{26}{3}\) …………..(1)
\(\frac{a}{r}\) . a . ar = \(\frac{-(-24)}{3}\)
a³ = 8
a = 2
From (1)
⇒ \(2\left(\frac{1+r+r^2}{r}\right)=\frac{26}{3}\)
⇒ 3(r² + r + 1) = 13r
⇒ 3r² – 10r + 3 = 0
⇒ 3r² – 9r – r + 3 = 0
⇒ 3r (r – 3) – 1(r – 3) = 0
⇒ (r – 3) (3r – 1) = 0
r = 3 (or) r = \(\frac{1}{3}\)

Case – 1:
a = 2, r = 3
The roots of the given equation are \(\frac{a}{r}\), a, ar = \(\frac{2}{3}\), 2, 6

Case – II:
a = 2, r = \(\frac{1}{3}\)
The roots of the given equation are \(\frac{a}{r}\), a, ar = 6, 2, \(\frac{2}{3}\).

Question 15.
Solve the equation 6x³ – 11x² + 6x – 1 = 0, the roots being in 1-LP.
Solution:
Given equation is 6x³ – 11x² + 6x – 1 = 0
The roots of 6x³ – 11x² + 6x – 1 = 0 are in H.P
The roots of \(6 \cdot \frac{1}{x^3}-11 \cdot \frac{1}{x^2}+\frac{6}{x}-1\) = 0 are in A.P.
6 – 11x + 6x² – x³ = 0
x³ – 6x² + 11x – 6 = 0
Let the roots be a – d, a, a + d
a – d + a + a + d = \(\frac{-(-6)}{1}\)
3a = 6
a = 2
(a – d) a (a + d) = \(\frac{-(-6)}{1}\) = 6
⇒ 2(a² – d²) = 6
⇒ 4 – d² = 3
⇒ d² = 1
⇒ d = 1
The roots of x³ – 6x² + 11x – 6 = 0 are a – d, a, a + d = 1, 2, 3.
∴ The roots of 6x³ – 11x² + 6x – 1 = 0 are 1, \(\frac{1}{2}\), \(\frac{1}{3}\).

Question 16.
Solve x³ – 7x² + 36 = 0, given one root being twice the other.
Solution;
Given equation is x’ – 7×2 + 36 = 0
Let α, β, γ be the roots of the given equation.
Now, α + β + γ = \(\frac{-(-7)}{1}\)
⇒ α + β + γ = 7 …………..(1)
αβ + βγ + γα = \(\frac{0}{1}\) = 0
⇒ αβ + βγ + γα = 0 ………….(2)
αβγ = \(\frac{-36}{1}\) = – 36
⇒ αβγ = – 36 ……………(3)
Given that one root being twke the other then β = 2α
(1) ⇒ α + 2α + γ = 7
⇒ 3α + γ = 7
⇒ α = 7 – 3α
(2) ⇒ α . 2α + 2αγ + αγ = 0
⇒ 2α + 3αγ = o
⇒ 2α² + 3α (7 – 3α) = 0
⇒ 2α² + 21α – 9α² = 0
⇒ 7α² – 21α = 0
⇒ α² – 3α =0
⇒ α (α – 3) = 0
⇒ α = 0 (or) α = 3
α = 0 does not satisfy the given equation.
∴ α = 3
If α =3
⇒ β = 6
γ = 7 – 3α
= 7 – 3 . 3
= 7 – 9
⇒ γ = – 2
∴ The roots of the given equation are 3, 6, – 2.

Question 17.
Solve x⁴ – 5x³ + 5x² + 5x – 6 = 0, given that the product of two of its roots is 3.
Solution:
Let α, β, γ, δ are the roots of given equation.
⇒ αβγδ = – 6
Given that the product of two roots is 3
αβ = 3
⇒ 3γδ = – 6
⇒ γδ = – 2
Let α + β = p, γ + δ = q
The quadratic equation whose roots are α, β is
x² – x(α + β) + αβ = 0
⇒ x² – px + 3 = 0 …………….(1)
The quadratic equation ol roots γ, δ is
x² – x(γ + δ) + γδ = 0
⇒ x² – qx – 2 = 0 ………………(2)
∴ x⁴ – 5x³ + 5x² + 5x – 6 = (x² – px + 3) (x² – qx – 2)
= x⁴ – qx³ – 2x² – px³ + pqx² + 2px + 3x² – 3qx – 6
= x⁴ + x ³ (- p – q) + x² (1 + pq) + x (2p – 3q) – 6
x³coeff. ⇒ – p – q = – 5
⇒ p + q = 5 ……………..(3)
xcoeff. ⇒ 2p – 3q = 5 …………..(4)
Solving (3) and (4)

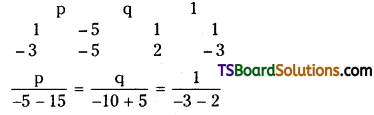
p = 4, q = 1
Sub. p = 4 in (1)
⇒ x² -4x + 3 = 0
⇒ x² – 3x – x + 3 = 0
⇒ x (x – 3) – 1 (x – 3) = 0
⇒ (x – 1) (x – 3) = 0
⇒ x – 1 = 0 (or) x – 3 = 0
⇒ x = 1 (or) x = 3
Sub.q = 1 in (2)
⇒ x² – x – 2 = 0
⇒ x² – 2x + x – 2 = 0
⇒ x (x – 2) + 1 (x – 2) = 0
⇒ (x + 1) (x – 2) = 0
⇒ x = 2 (or) x = – 1
The roots of given equation are – 1, 1, 2, 3.

Question 18.
Solve 9x³ – 15x² + 7x – 1 = 0, given that two of its roots are equal.
Solution:
Given equation is 9x³ – 15x² + 7x – 1 = 0
Let α, β, γ are the roots of 9x – 15x² + 7x – 1 = 0
Now, α + β + γ = \(\frac{-(-15)}{9}=\frac{5}{3}\) ⇒ 1
⇒ αβ + βγ + γα = \(\frac{7}{9}\) …………….(2)
αβγ = \(\frac{-(-1)}{9}=\frac{1}{9}\) …………(3)
Given α = β; (1)
⇒ 2α + γ = \(\frac{5}{3}\) ……………(4)
(2) ⇒ α² + αγ + γα = \(\frac{7}{9}\)
α² + 2αγ = \(\frac{7}{9}\)
γ = \(\frac{7}{18 \alpha}-\frac{\alpha}{2}\) ………….(5)
From (4) 2α + \(\frac{7}{18 \alpha}-\frac{\alpha}{2}=\frac{5}{3}\)
⇒ \(\frac{36 \alpha^2+7-9 \alpha^2}{18 \alpha}=\frac{5}{3}\)
⇒ 27α² – 30α + 7 = 0
⇒ 27α² – 21α – 9α + 7 = 0
⇒ 3α (9α – 7) – 1 (9α – 7) = 0
⇒ (3α – 1) (9α – 7) = 0
∴ α = \(\frac{1}{3}\), β = \(\frac{7}{9}\)
α = does not satisfy the given equation.
∴ α = \(\frac{1}{3}\), β = \(\frac{1}{3}\)
(4) ⇒ \(\frac{2}{3}\) + γ = \(\frac{5}{3}\)
γ = \(\frac{5}{3}-\frac{2}{3}=\frac{3}{3}\) = 1
γ = 1
∴ The roots of the given equation are \(\frac{1}{3}\), \(\frac{1}{3}\), 1.

Question 19.
Solve x³ – 3x² – 16x + 48 = 0.
Solution:
Let f(x) = x³ – 3x² – 16x + 48 = 0
If x = 3
⇒ f(3) = 27 – 27 – 48 + 48 = 0
Hence 3 is a root of f(x) = 0.
Now, we divide f(x) by x – 3 using synthetic division

∴ The quotient is x² – 16 and the remainder is zero.
∴ f(x) = x³ – 3x² – 16x + 48
= (x – 3) (x² – 16)
= (x – 3) (x + 4) (x – 4)
∴ The roots are 3, – 4, 4.

Question 20.
Solve the equation 4x³ – 13x² – 13x + 4 = 0.
Solution:
Given equation is 4x³ – 13x² – 13x 4 = 0.
f(x) = 4x³ – 13x² – 13x + 4
If x = – 1
⇒ f(- 1) = 4(- 1)³ – 13(- 1)² – 13(- 1) + 4
= – 4 – 13 + 13 + 4 = 0
∴ (x + 1) is a factor of f(x).
Now, on dividing 4x³ – 13x² – 13x + 4 = 0 by x + 1.

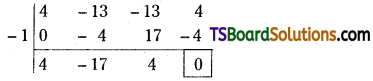
Quotient is 4x² – 17x + 4
4x² – 17x + 4 = 0
4x² – 16x – x + 4 = 0
=4x (x – 4) – 1 (x – 4) = 0
(4x – 1) (x – 4) = 0
x = \(\frac{1}{4}\), x = 4
∴ 4x³ – 13x² – 13x + 4 = (x + 1) (x – 4) (4x – 1)
∴ The roots of the given equation are – 1, 4, 1/4.

Question 21.
Find the polynomial equation whose roots are the translates of those of the equatior x⁵ – 4x⁴ + 3x² – 4x + 6 = 0 by – 3.
Solution:
Let f(x) = x⁵ – 4x⁴ + 3x² – 4x + 6
∴ The required equation is f(x + 3) =0
∴ f(x+3) = A₀x⁵ + A₁x⁴ + A₂x³ + A₃x² + A₄x + A₅
The coefficients A₀, A₁, A₂, A₃, A₄, A₅ can be obtained as follows.

∴ Required equation ¡s f(x + 3) = 0
x⁵ + 11x⁴ + 42x³ + 57x² – 13x – 60 = 0.

Question 22.
Solve the equation x⁴ + 2x³ – 16x² – 22x + 7 = 0 given that 2 – √3 is one of its roots.
Solution:
Given equation is x⁴ + 2x³ – 16x² – 22x + 7 = 0 ……………..(1)
Let f(x) = x⁴ + 2x³ – 16x² – 22x + 7
Given 2 – √3 is a root of (1).
⇒ 2 + √3 is also a root of (1).
(∵ coefficients of (1) are rational)
∴ (x – (2 – √3)) (x – (2 + √3)) is a factor of f(x).
(x² – 4x + 1)is a factor of f(x).
We divide f(x) by x² – 4x 1.
By synthetic division,

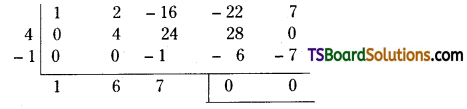
∴ f(x)=(x² – 4x +1 ) (x² + 6x + 7)
∴ Equation (1)
z(x² – 4x + 1) (x² + 6x + 7) = 0
=x² – 4x + 1 = 0 or x² + 6x + 7 = 0
x = 2 ± √3 or x = – 3 ± √2
∴ The roots of the given equation are 2 ± √3, – 3 ± √2.

Question 23.
If α, β, γ are the roots of x³ + px² + qx + r = 0, then form the monic cubic equation whose roots are α(β + γ), β(γ + α), γ(α + β).
Solution:
Given equation is x³ + px² + qx + r = 0
Since α, β, γ are the roots of the equation.
x³ + px² + qx + r = 0 then
s₁ = α + β + γ = \(\frac{-p}{1}\) = – p;
s₂ = αβ + βγ + γα = \(\frac{q}{1}\) = q;
s₃ = αβγ = \(\frac{-r}{1}\) = – r
Let s₁ = Σ α(β + γ)
= Σ (αβ + αγ) = Σ αβ + Σ αγ = Σ αβ + Σ αβ = 2Σ αβ = 2q
s₂ = Σ α(β + γ) . β(γ + α)
= Σ αβ (- p – α) (- p – β)
= Σ αβ (p + α) (p + β)
= Σ αp (p² + p(α + β) + αβ)
= Σ αp [p² + p(- p – γ) + ap]
= Σ αβ [p² – p² – pγ + αβ]
= – pΣ αβγ + Σ αβ
= – p(3αβγ) + (αβ + βγ + γα)² – 2αβγ(α + β + γ)
= – 3p (- r) + q² – 2 (- r) (- p)
= 3pr + q² – 2pr
= q² + pr
s₃ = α (β + γ) β (γ + α) γ (α + β)
= αβγ(- p – α) (- p – β) (- p – γ)
= – αβγ [(p + α) (p + β) (p + γ)]
= – αβγ [(p² + pα + pβ + αβ) (p + γ)]
= – αβγ [p³ + p²α + p²β + pαβ + p²γ + pαγ + pβγ + αβγ]
= – αβγ [p³ + p² (α + β + γ) + p(αβ + βγ + γα) + αβγ]
= – (- γ)[p³ + p² (- p) + p(q) + (- r)]
= γ [p³ – p³ + pq – r]
= pqr – r²
∴ The monic cubic equation whose roots are α (β + γ), β(γ + α), γ(α + β) is
x³ – s₁x² + s₂x – s₃ = 0
x³ – 2qx² + (q² + pr) x – r (pq – r) = 0.

Question 24.
If α, β, γ are the roots of x³ – 6x² + 11x – 6 = 0, then find the equation whose roots are α² + β², β² + γ², γ² + α².
Solution:
Let f(x) = x³ – 6x² + 11x – 6
If x = 1 then f(1) = 1 – 6 + 11 – 6 = 12 – 12 = 0
(x – 1) is the factor of f(x)

x² – 5x + 6 = 0
⇒ x² – 3x – 2x + 6 = 0
⇒ x (x – 3) – 2 (x – 3) = 0
⇒ (x – 2) (x – 3) = 0
⇒ x – 2 = 0; x – 3 = 0
Therefore, x³ – 6x² + 11x – 6 = 0
⇒ (x – 1) (x – 2) (x – 3) = 0
⇒ x = 1, 2, 3
Since α, β, γ are the roots of x³ – 11x² + 11x – 6 = 0
Then, α = 1; β = 2; γ = 3.
Now, α² + β² = 1 + 4 = 5;
β² + γ² = 4 + 9 = 13;
γ² + α² = 9 + 1 = 10
The equation having roots 5, 13, 10 is (x – 5) (x – 13) (x – 10) = 0
= (x² – 18x + 65) (x – 10) = 0
x³ – 18x² + 65x – 10x² + 180x – 650 = 0
x³ – 28x² + 245x – 650 = 0

Question 25.
If α, β, γ are the roots of x³ – 7x + 6 = 0, then find the equation whose roots are (α – β)², (β + γ)², (γ + α)².
Solution:
Let f(x) = x³ – 7x + 6
If x = 1 then f(1) = 1 – 7(1) + 6 – 7 – 7 = 0
∴ (x – 1) is a factor of f(x)
x² + x – 6 = 0
⇒ x² + 3x – 2x – 6 = 0

x (x + 3) – 2 (x + 3) = 0
(x + 3) (x – 2) = 0
∴ x³ – 7x + 6 = 0
⇒ (x + 3) (x – 1) (x – 2) = 0
⇒ x = – 3, 1, 2
Since α, β, γ are the roots of x³ – 7x + 6 = 0
then, α = – 3; β = 1; γ = 2.
Now, (α – β)² = (- 3 – 1)² = 16;
(β – γ)² = (1 – 2)² = 1;
(γ – α)² = (4 + 9)² = 25
The equation having roots 16, 1, 25 is (x – 16) (x – 1) (x – 25) = 0
(x² – 1 7x + 16) (x² – 25) = 0
x³ – 17x² + 16x – 25x² + 465x – 400 = 0
x³ – 42x² + 441x – 400 = 0.

Question 26.
Solve x³ – 9x² + 14x + 24 = 0 given that two of the roots are in the ratIo 3: 2.
Solution:
Let the roots be 3α, 2α, β
3α + 2α + β = \(\frac{-(-9)}{1}\) = 9
⇒ 5α + β = 9
⇒ β = 9 – 5α ……………..(1)
3α . 2α + 2αβ + 3αβ = \(\frac{14}{1}\)
⇒ 6α² + 5αβ = 14
6α² + 5α – 14 = 0
⇒ 6α² + 5α (9 – 5α)-14 =0
6α² + 45α – 25α – 14 = 0
⇒ 19α² + 45α – 14 = 0
⇒ 19α² – 45α + 14 = 0
⇒ 19α² – 38α – 7α + 14 = 0
⇒ 19α(α – 2) – 7(α – 2) = 0
(α – 2) (19α – 7) = 0
α = 2 (or)
α = \(\frac{7}{19}\)
⇒ α = \(\frac{14}{19}\)
⇒ 2α = does not satisfy the given equation.
∴ α = 2
3α = 6
2α = 4
(1) ⇒ β = 9 – 5(2)
(2) ⇒ 9 – 10 = – 1
β = – 1
∴ The roots of the given equation are 6, 4,- 1.

Question 27.
Solve the equation x⁴ – 6x³ + 13x² – 24x + 36 = 0 given that they have multiple roots.
Solution:
Let f(x) = x⁴ – 6x³ + 13x² – 24x + 36 = 0
if x = 3 then 81 – 6(27) + 13(9) – 24 (3) + 36
= 81 – 162 + 117 – 72 + 36
= – 234 + 234 = 0
∴ x = 3 is a root of f(x) = 0
Let g(x) = x³ – 3x² + 4x – 12 = 0
If x = 3 then g(3) = 3³ – 3(3²) + 4(3) – 12
= 27 – 27 + 12 – 12 = 0

Let, h(x) = x² + 4 = 0
⇒ x² = – 4
x = ± √4 = ± 2
The roots of the given equation are 3, 3, ± 2i.
Multiple root is 3.

Question 28.
Solve the equation 8x³ – 20x² + 6x + 9 = 0 given that the equation has multiple roots.
Solution:
Given equation is 8x³ – 20x² + 6x + 9 = 0 ………………(1)
Let f(x) = 8x³ – 20x² + 6x + 9
f’(x) = 24x² – 40x + 6
= 2(12x² – 20x + 3)
= 2 (2x – 3) (6x – 1)
\(f\left(\frac{3}{2}\right)=8\left(\frac{27}{8}\right)-20\left(\frac{9}{4}\right)+6\left(\frac{3}{2}\right)+9\)
= 27 – 45 + 9 + 9 = 0
∴ f(\(\left(\frac{3}{2}\right)\)) = 0
∴ f(x) and f’(x) has a common factor ‘2x – 3’.
∴ \(\frac{3}{2}\) is a multiple root of f(x) = 0.
By synthetic division,

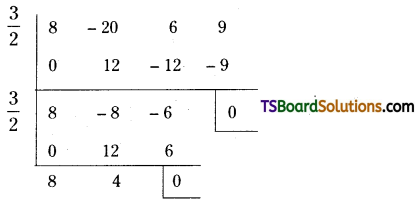
∴ 8x³ – 20x² + 6x + 9 = 0
=(x – \(\frac{3}{2}\))² (8x + 4) = 0
x = \(\frac{3}{2}\) or x = \(\frac{-1}{2}\)
∴ The roots of given equation are \(-\frac{1}{2}, \frac{3}{2}, \frac{3}{2}\).

Question 29.
Solve 6x⁴ – 13x³ – 35x² – x + 3 = 0, given that one of its roots is 2 + √3.
Solution:
Given equation is 6x⁴ – 13x³ – 35x² – x + 3 = 0
Since 2 + √3 is a root of it, 2 – √3 is also a root.
The quadratic factor of these two roots is (x – (2 + √3)) (x – (2 – √3))
= ((x – 2) – √3) ((x – 2) + √3)
= (x – 2)² – 3
= x² + 4 – 4x – 3
= x² – 4x + 1
On dividing, 6x⁴ – 13x³ – 35x² – x + 3 by x² – 4x + 1.

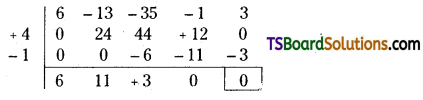
∴ Quotent is 6x² + 11x + 3
6x² + 11x + 3 = 0
6x² + 9x + 2x + 3 = 0
3x (2x + 3) + 1 (2x + 3) = 0
= (3x + 1) (2x + 3) = 0
x = \(\frac{-1}{3}\), x = \(\frac{-1}{2}\)
∴ The roots of the given equation are \(\frac{-1}{2}\), \(\frac{-1}{2}\), 2 ± √3.

Question 30.
Solve the equation x⁴ + 2x³ – 5x² + 6x + 2 = 0 given that 1 + i is one of its roots.
Solution:
Given equation is x⁴ + 2x³ – 5x² + 6x + 2 = 0
Since 1 + i is a root of the given equation
then 1 – i is also a root of it.
The quadratic factor to these two roots is
(x – (1 + i)) ((x – (1 – i)) = 0
((x – 1) – i) ((x – 1) + i) = (x – 1) – i
x² + 1 – 2x + 1 = x⁴ – 2x + 2
On dividing x⁴ + 2x³ – 5x² 6x + 2 by x² – 2x + 2

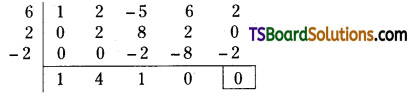
Quotient is x² + 4x + 1
x² + 4x + 1 = 0
x = \(\frac{-4 \pm \sqrt{1-4}}{2(1)}\) = – 2 ± √3
∴ The roots of the given equation are 1 + i, 1 – i, – 2 ± √3.

Question 31.
Solve x⁴ – 4x² + 8x + 35 = 0, given that 2 + √3 is a root. [AP – Mar. 2015]
Solution:
Given equation is x⁴ – 4x² + 8x + 35 = 0
Since 2 + i√3 is a root of it,
2 – i√3 is also a root.
The quadratic factor to these two roots is (x – (2 + i√3)) (x – (2 – i√3))
= ((x – 2) – i√3) ((x – 2) + i√3)
= (x – 2)² (i√3)²
= x² + 4 – 4x + 3
= x² – 4x + 1
On dividing x⁴ – 4x² + 8x + 35 with x² – 4x + 7 we get,

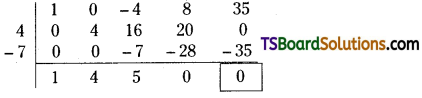
∴ Quotient is x² + 4x + 5
x² + 4x + 5 = 0
x = \(\frac{-4 \pm \sqrt{16-20}}{2(1)}=\frac{-4 \pm \sqrt{-4}}{2}\) = – 2
∴ The roots of the given equation are 2 ± i√3, – 2 ± i.

Question 32.
Solve the equation x⁴ – 6x³ + 11x² – 10x + 2 = 0, given that 2 + √3 is a root of the equation.
Solution:
Given equation is x⁴ – 6x³ + 11x² – 10x + 2 = 0
Since 2 + √3 is a root of it, 2 – √3 is also a root.
The quadratic factor to these roots is (x – (2 + √3)) (x – (2 – √3))
= ((x – 2) – √3) ((x – 2) + √3)
= (x – 2)² – 3
= x² + 4 – 4x – 3
= x² – 4x + 1

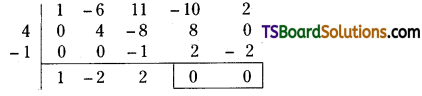
∴ Quotient is x² – 2x + 2
∴ x² – 2x + 2 = 0
x = \(\frac{-(-2) \pm \sqrt{4-4(2)}}{2(1)}\)
= \(\frac{2 \pm 2 \mathrm{i}}{2}\) = 1 ± i.
∴ Roots of given equation are 2 ± √3, 1 ± i.

Question 33.
Find the polynomial equation whose roots are the translates of those of the equation x⁴ – 5x³ + 7x² – 17x + 11 = 0 by – 2. [TS – May 2016]
Solution:
Let f(x) = x⁴ – 5x³ + 7x² – 17x + 11 = 0
∴ The required equation is f(x + 2) = 0
Now, f(x + 2) = A₀x⁴ + A₁x³ + A₂x² + A₃x + A₄
Then, the coefficients A₀, A₁, A₂, A₃, A₄ can
be obtained as follows

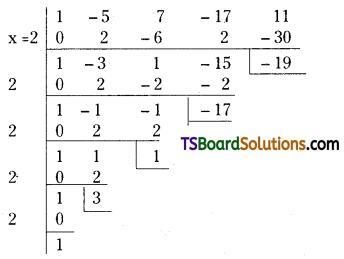
∴ Required equation is f(x + 2) = 0
x⁴ + 3x³ + x² – 17x – 19 = 0.

Question 34.
Find the polynomial equation whose roots are the translates of the roots of the equation x⁴ – x³ – 10x² + 4x + 24 = 0 by 2.
Solution:
Let f(x) = x⁴ – x³ – 10x² + 4x + 24 = 0
∴ Required equation is f(x -2) = 0
Let f(x – 2) = A₀x⁴ + A₁x³ + A₂x² + A₃x + A₄.
The coefficients A₀, A₁, A₂, A₃, A₄ can be obtained as follows

∴ Required equation is f(x – 2) = 0
x⁴ – 9x³ + 40x² – 80x + 80 = 0.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 5 Hyperbola will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Hyperbola Formulas

→ Hyperbola is a conic which is the locus of a point that moves so that the ratio of the distance from a fixed point to its distance from a fixed line is greater than 1.

→ Equation of hyperbola in the standard form is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 centre at (0, 0) and foci (±ae, 0) directrices x = ± \(\frac{a}{e}\) and eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)

→ Various fonns of the hyperbola :

Hyperbola	Conjugate hyperbola
S = \( \frac{x^2}{a^2}-\frac{y^2}{b^2} \) – 1 = 0	S’ = \( \frac{x^2}{a^2}-\frac{y^2}{b^2} \) + 1 = 0
1. Transverse axis is along * X – axis (y = 0) and its length is 2a.	1. Transverse axis is along Y – axis (x = 0) and its length is 2b.
2. Conjugate axis is along Y-axis (x = 0) and its length is 2b.	2. Conjugate axis is along X – axis (y – 0) and its length is 2a
3. Coordinates of the centre C = (0, 0).	3. Coordinates of the centre C = (0, 0).
4. Foci S = (±ae, 0)	4. Foei S’ = (0, ± be)
5. Equation of the directrices x = ±\(\frac{a}{e}\)	5. Equation of the directrices y = ±\(\frac{b}{e}\)
6. Eccentricity e = \( \sqrt{\frac{a^2+b^2}{a^2}} \)	6. Eccentricity e = \( \sqrt{\frac{a^2+b^2}{b^2}} \)

→ If the centre is at (h, k) and the axes of the hyperbola are parallel to the coordinate axis.

→ If P is any point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 and foci are S and S’ then S’P – SP = 2a.

→ Equation of rectangular hyperbola whose eccentricity is √2 is x² – y² = a².

→ The equation of auxiliary circle of the hyperbola S = 0 is x² + y² = a²,

→ x = a sec θ, y = b tan θ are the parametric equations of hyperbola.

→ The condition for a straight line y = mx + c to be a tangent to the hyperbola S = 0 is c² = a²m² – b².

→ y = mx ± \(\) is always a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 and point of contact is \(\left(-\frac{a^2 m}{c},-\frac{b^2}{c}\right)\) and \(\left(\frac{a^2 m}{c}, \frac{b^2}{c}\right)\)

→ The equation of tangent at (x₁, y₁) to S = 0 is \(\frac{x_1}{a^2}-\frac{y y_1}{b^2}\) = 1.

→ The equation of normal at (x₁, y₁) to S = 0 is \(\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}\) = a² + b²

→ Equation of tangent at the point (asec θ, btan θ) is \(\frac{x}{a}\)sec θ – \(\frac{y}{b}\)tan θ = 1.

→ Equation of normal at the point P(θ) is \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b².

→ The equation of the asymptotes of a hyperbola S = 0 are y = ±\(\frac{b}{a}\) x and the combined equation of asymptotes is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 0

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 4 Ellipse will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Ellipse Formulas

→ An ellipse is the locus of a point whose distances from a fixed point and a fixed straight line are in a constant ratio ‘e’ which is less than unity. The fixed point and the fixed straight line are called the focus and the directrix of ellipse respectively.

→ Equation of an ellipse in the standard form is – 1, (a > b). Centre = (0, 0)
Foci = (± ae, 0); Directrix, x = ±\(\frac{\mathrm{a}}{\mathrm{e}}\) and Eccentricity, e = \(\sqrt{\frac{a^2-b^2}{a^2}}\)

→ Various forms of the ellipse Form:
(i) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (a > b > 0)

(ii) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (0 < a < b)

(iii) \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 (a > b > 0)

(iv) \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 (0 < a < b)

→ If P is any point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, (a > b) and foci are S, S’, then SP + S’P = 2a.

→ The equation of the auxiliary circle of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, (a > b) is x² + y² = a².

→ Parametric equations of ellipse S = 0 are x = a cos θ, y = b sin θ and θ is called the parameter.

→ If P(x₁, y₁) is a point on the plane of the ellipse, then P lies outside, on or inside the ellipse according as Sn is positive, zero or negative.

→ The condition for the straight line y = mx + c to touch the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is (or) tangent to the ellipse is c² = a²m² + b².

→ y = mx ± \(\sqrt{a^2 m^2+b^2}\) is always a tangent to the ellipse S = 0 at \(\sqrt{a^2 m^2+b^2}\) and \(\left(\frac{a^2 m}{c}, \frac{-b^2}{c}\right)\)

→ The equation of the tangent at P (x₁, y₁)to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is \(\frac{\mathrm{x} \mathrm{x}_1}{a^2}+\frac{\mathrm{y} \mathrm{y}_1}{\mathrm{~b}^2}\) – 1 = 0

→ The equation of the normal to the ellipse at P (x₁, y₁) is \(\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}\) = a² – b²

→ Equation of the tangent at P (θ) i.e., P (a cos θ, b sin θ) to the ellipse S = 0 is \(\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}\) = 1.

→ Equation of the normal at P(θ) to the ellipse S = 0 is \(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}\) = a² – b²
where θ ≠ 0, \(\frac{\pi}{2}\), π, \(\frac{3 \pi}{2}\)

→ Eqilation of director circle of the ellipse S = 0 is x² + y² = a² + b²

→ If P(x₁, y₁) Is an external point to the ellipse S = 0, then the equation of chord of contact of P w.r.t ellipse S = 0 is \(\frac{x x_1}{a^2}+\frac{y y_1}{b^2}\) = 1.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 7 Definite Integrals will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Definite Integrals Formulas

→ If F(x) is an indefinite integral (or) anti-derivative of a function f(x) defined on [a, b] then
\(\int_a^b\)f(x) dx = F(b) – F(a) …………….. (1).
The symbol \(\int_a^b\)f (x) dx is called the definite integral of f(x) from x = a to x = b. The numbers ’a’ and ’b’ are called the limits of integration, ’a’ is called the lower limit and ’b’ is called the upper limit. If we use the notation \([\mathrm{F}(\mathrm{x})]_{\mathrm{a}}^{\mathrm{b}}\) to denote
F(b) – F(a), then from (1) \(\int_a^b\)f (x) dx = \([\mathrm{F}(\mathrm{x})]_{\mathrm{a}}^{\mathrm{b}}\) = [(F(x) at x = b) – (F(x) at x = a)].

→ Fundamental properties of definite integrals:
Property – 1 : \(\int_a^a\) f (x) dx = 0

Property-2: \(\int_a^b\) f(x)dx = \(\int_a^b\)f(t)dt

Property-3: \(\int_a^b\)f(x)dx = – \(\int_b^a\)f(x)dx

Property-4: \(\int_a^b\)f(x)dx = \(\int_a^c\)f(x)dx + \(\int_c^b\)f(x)dx, if a < c < b

Property-5: \(\int_0^a\)f (x)dx = \(\int_0^a\)f (a – x)dx

Property- 6: \(\int_{-a}^a\)f(x) dx = 2\(\int_0^a\)f(x)dx, if f(x) is even
= 0, if f(x) is odd

Property – 7: \(\int_0^{2 a}\)f(x) dx = 2\(\)f(x)dx, if f(2a – x) = f(x)
= 0, if f(2a – x) = – f(x)

Properly – 8: \(\int_a^b\)f(x)dx = \(\int_a^b\)f(a + b – x)dx

Properly-9: \(\int_0^{n a}\)f (x)dx = n\(\int_0^{a}\)f(x)dx, if f(a + x) = f(x)

Properly -10: \(\int_0^{\infty}\)f(x)dx = \({Lt}_{t \rightarrow \infty} \int_0^t\)f(x)dx and \(\int_{-\infty}^a\) f(x)dx = \({Lt}_{t \rightarrow-\infty} \int_t^a\)f(x)dx
and \(\int_{-\infty}^{\infty}\) f(x)dx = \({Lt}_{t \rightarrow \infty} \int_a^t\)f(x)dx + \({Lt}_{t \rightarrow-\infty} \int_t^a\)f(x)dx

Properly -11: |\(\int_a^b\)f(x) dx| ≤ \(\int_a^b\) |f(x)|dx

Properly -12: If f(x) ≥ 0, ∀x ∈ [a, b], then \(\int_a^b\)f(x)dx ≥ 0 and if f(x) ≥ g(x), ∀ x ∈ [a, b] then \(\int_a^b\)f(x)dx ≥ \(\int_a^b\) g(x)dx

→ Reduction Formulae:

• If I_n = \(\int_0^{\pi / 2}\)sinⁿ dx, then I_n = \(\frac{n-1}{n}\)I_n-2
• If I_n = \(\int_0^{\pi / 2}\)cosⁿ dx, then I_n = \(\frac{n-1}{n}\)I_n-2
• If I_n = \(\int_0^{\pi / 4}\)tanⁿ dx, then I_n = \(\frac{1}{n-1}\)I_n-2
• If I_n = \(\int_0^{\pi / 4}\)secⁿ dx, then I_n = \(\frac{(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_n = \(\int_{\pi / 4}^{\pi / 2}\)cotⁿ dx, then I_n = \(\frac{1}{n-1}\) – I_n-2
• If I_n = \(\int_{\pi / 4}^{\pi / 2}\)cosecⁿ dx, then I_n = \(\frac{-(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2
• If I_m,n = \(\int_0^{\pi / 2}\)sin^mx. cosⁿxdx then I_m,n = \(\frac{-(\sqrt{2})^{n-2}}{n-1}+\frac{n-2}{n-1}\)I_n-2

Let m and n be positive integers, then

Let n be an integer greater than or equal to 2.

Areas:
→ Let f be a continuous function on [a, b]. Then the area of the region bounded by curve y = f(x) with X – axis between the lines x = a and x = b is
(i) \(\int_a^b\)f(x)dx, if f(x) ≥ 0

(ii) –\(\int_a^b\)f(x)dx, if f(x) ≤ 0

→ Let a < c < b and if f(x) ≥ 0 on [a, cl and f(x) ≤ 0 on [b, C]. Then the area of the region bounded by the curve y = f(x) wIth X- axis between lines x = a and x = b is
\(\int_a^c\)f(x) dx – \(\int_c^b\)f(x) dx

→ The area of the region bounded by the curve x = f(y) with Y – axis between the lines y = c and y = d is
(i) \(\int_c^d\)f(y) dy, if f(y) ≥ 0

(ii) \(\int_c^d\)f(y) dy, If f(y) ≤ 0

→ Let c < e < d and If f(y) ≥ 0 on [c, e] and f(y) ≤ 0 on [e, d]. Then the area of the region bounded by the curve x = f(y) with Y-axis between the lines y = c and y =d is

\(\int_c^e\)f(y)dy – \(\int_d^e\)f(y) dy

→ The area of the region bounded by the curves y f(x), g(x) = y between the lines x = a and x = b is
(i) \(\int_a^b\)[f(x) – g(x)]dx, if f(x) ≥ g(x)

(ii) \(\int_a^b\)[g(x) – f(x)]dx; if f(x) ≤ g(x)

→ The area of the region bounded by the curves x = f(y), x = g(y) between the lines y = c and y = d is x = g(x) x = f(x)
(i) \(\int_c^d\)[f(y) – g(y)]dy, if f(y) > g(y)

(ii) \(\int_c^d\)[g(y) – f(y)]dy, if f(y) ≤ g(x)

→ Limit As A Definite Integral
Definite Integral as a limit of summation:
Definition :Let I be a continuous function on [a, b]. Divide [a, b] into ‘n’ sub Intervals ,[x₀, x₁]……….. [x_(n-1) , x_n] where a = x₀ < x₁ < x₂ < ……………… < x_n = b
Let, ξr ∈ [x_r-1, x] for r 1, 2 , ……………… n.

→ If \({Lt}_{n \rightarrow 0} \sum_{r=1}^n\) f(ξ_r) (x_r – x_r-1) exists, then f(x) is called an integrable function on [a, b] and the limit is called definite integral of f on [a, b]. It is denoted by \(\)f(x) dx
Note:
To simplify calculation we can take all sub intervals to be equal length, h
Then h = \(\frac{b-a}{n}\) and \(\int_a^b\)f(x)dx = \({Lt}_{n \rightarrow \infty} h \sum_{r=1}^n f\left(\xi_Y\right)\)

Also we take, ξ_r = x_r-1, then ξ_r = a + (r – 1)h and hence.
\(\int_a^b\)f(x)dx = \({Lt}_{n \rightarrow \infty} h \sum_{r=1}^n\)f(a +(r – 1)h] = \({Lt}_{h \rightarrow 0} h \sum_{r=1}^h\)f[a + (r – 1)h]

If a = 0, b = 1, then \(\int_0^1\)f(x)dx = \({Lt}_{n \rightarrow \infty} \frac{1}{n} \sum_{r=1}^n f\left(\frac{r-1}{n}\right)+\left(\frac{r-1}{n}\right)={Lt}_{n \rightarrow 0} \frac{1}{n} \sum_{r=0}^{n-1} f\left(\frac{r}{n}\right)\)

If a = 0, b = p then \(\int_0^P\)f(x)dx = \({Lt}_{n \rightarrow \infty} \frac{1}{n} \sum_{r=1}^{n p}\left(\left(\frac{r-1}{n}\right)\right.\)

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 8 Differential Equations will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Differential Equations Formulas

→ An equation involving one dependent variable and its derivatives with respect to one or more independent variables is called a differential equation. If the equation contains only one independent variable then it is called an ordinary differential equation and if it contains more than one independent variable then it is called a partial differential equation,

→ If the differential equation is of the form f(x) dx + g(y)dy = 0 then its solution is ∫ f(x) dx + ∫ g(y) dy = 0.

→ The order of a differential equation is the order of the highest derivative occurring in it and the largest exponent of the highest order derivative in the equation is called the degree of the differential equation.

→ By eliminating the arbitrary constants in the given equation, we can formulate the differential equation.

→ If the differential equation is of the form \(\frac{d y}{d x}=\frac{f(x, y)}{g(x, y)}\), where f and g are homogeneous functions of x and y of same degree, then we put y = vx and obtain the form Φ(υ) dυ = \(\frac{d x}{x}\) and on integration gives the solution.

→ If the differential equation is of the form
\(\frac{d y}{d x}=\frac{a x+b y+c}{a^{\prime} x+b^{\prime} y+c^{\prime}}\), where a, b, c, a, b, c are constants.

• If b = – a’ then its solution can be obtained by term by term integration after regrouping.
• If \(\frac{a}{a^{\prime}}=\frac{b}{b^{\prime}}\) = m then we put ax + by = v and bring it in the form Φ(υ) dυ = \(\frac{d x}{x}\) and then integrate.
• If \(\frac{a}{a^{\prime}} \neq \frac{b}{b^{\prime}}\), then put x = X + h, y = Y + k (h, k are obtained by solving ah + bk + c = 0 and
  a’h + b’k + c’ = 0 and bring it to the form \(\)
  Then take Y = VX and obtain Φ(V) dV = \(\frac{d X}{X}\) and then integrate.

→ If the differential equation is of the form \(\frac{d y}{d x}\) + Py = Q then the solution is
ye_∫pdx = C + ∫Q_e∫pdxdx.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 3 Parabola will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B Parabola Formulas

→ The locus of a point moving on a plane such that its distance from a fixed point and a fixed straight line in the plane are in a constant ratio ‘e’ is called a conic and e is called the eccentricity of the conic. Fixed point is called focus and the fixed straight line is called the directrix. If e = 1, the conic is called a Parabola.

→ Equation of a parabola in the standard form is y2 = 4ax (a > 0) with focus (a, 0), axis y = 0, equation of directrix is x + a = 0 and length of the latus rectum is 4a.

→ Various different forms of parabola (general)
Table: 1
(i) Form: y² = 4ax
Vertex: (0, 0)
Focus: (a, 0)
Directrix: x + a = 0
Axis: y = 0

(ii) Form: x² = 4ay
Vertex: (0, 0)
Focus: (0, a)
Directrix: y + a = 0
Axis: x = 0

(iii) Form: y² = -4ax
Vertex: (0, 0)
Focus: (-a, 0)
Directrix: x – a = 0
Axis: y = 0

(iv) Form: x² = -4ay
Vertex: (0, 0)
Focus: (0, -a)
Directrix: y – a = 0
Axis: x = 0

Table: 2
(i) Form:(y – k)² = 4a(x – h)
Vertex: (h, k)
Focns: (h + a, k)
Axis: y = k
EquaffonotDlrectrlx: x – h + a = 0

(ii) Form: (y – k)² = -4a(x – h)
Vertex: (h, k)
Focus: (h – a, k)
Axis: y – k = 0
Equation of Directrix: x – h – a = 0

(iii) Form: (x – h)² = -4a(y – k)
Vertex: (h, k)
Focus: (h, k – a)
Axis: x – h = 0
Equation of Directrix : y – k -a = 0

(iv) Form : (x – h)² = 4a(y – k)
Vertex: (h, k)
Focus: (h, a + k)
Axis: x – h = 0
Equation of Directrix: y – k + a = 0

(v) Form: (x – α)² + (y – β)² = \(\frac{(l x+m y+n)^2}{l^2+m^2}\)
Vertex : Point A
Focus: (α, β)
Axis: m(x – α) – l(y – β) = 0
Equation of Directrix: lx + my + n = 0

→ The equation of parabola when its axis is parallel to X – axis is x = ly² + my + n and when axis is parallel to Y- axis is y = lx² + mx + n.

→ Focal distance of a point (x₁, y₁) on the parabola y² = 4ax is x₁ + a.

→ Parametric equations of the parabola are x = at², y = 2at.

→ P(x₁, y₁) lies outside, on or inside the parabola y² = 4ax according as S₁₁ \(\frac{\geq}{<}\) 0.

→ y = mx + c (m * 0) is a tangent to the parabola y² = 4ax when c = a/m.

→ y = mx + a/m (m ≠ 0) is always a tangent to the parabola y² = 4ax and point of contact is \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)

→ Equation of the tangent at the point (x₁, y₁) on the parabola y² = 4ax is yy₁ = 2a (x + x₁) or S₁ = 0. .

→ Equation of the normal at the point (x₁, y₁) on the parabola S = 0 is y – y₁ = \(-\frac{y_1}{2 a}\) (x – x₁).

→ Equation of tangent at a point ‘t’ i.e„ (at², 2at) on y² = 4ax is x = yt + at².

→ Equation of normal at a point ‘t’ on y² = 4ax is y + xt = 2at + at³.

Learning these TS Inter 2nd Year Maths 2B Formulas Chapter 2 System of Circles will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2B System of Circles Formulas

→ We denote circles by S = x² + y² + 2gx + 2fy + c = 0 and S’ = x² + y² + 2g’x + 2f’y + c’ = 0.

→ If C₁, C₂ are the centres and r₁, r₂ are radii of two intersecting circles S = 0 and S’ = 0 and C₁C₂ = d then if θ is the angle between them, then cos θ = \(\frac{d^2-r_1^2-r_2^2}{2 r_1 r_2}\)

→ If 0 is the angle between two intersecting circles S = 0 and S’ = 0, then
cos θ = \(\frac{c+c^{\prime}-2 g g^{\prime}-2 f^{\prime}}{2 \sqrt{g^2+f^2-c} \sqrt{g^2+f^2-c^{\prime}}}\)

→ Two circles S = 0 and S’ = 0 are orthogonal ⇔ 2(gg’ + ff’) = c + c’.

→ If S = 0, S’ = 0 are any two intersecting circles and λ, µ are two real numbers such that λ + µ ≠ 0 and λS + µS’ = 0 represents a circle passing through the intersection of circles S = 0, S’ = 0.

→ If S = 0, S’ = 0 are any two intersecting circles and ke R (≠ -1) then S + kS’ = 0 represents a circle passing through their point of intersection.

→ If S = 0 and a straight line L = 0 intersect, then for any real number k, S + kL = 0 represents a circle passing through their intersection.

→ The equation of common chord of two intersecting circles S = 0, S’ = 0 is S – S’ = 0.

→ The equation of common tangent at the point of contact when the circles S = 0, S’ = 0 touch each other is S – S’ = 0.

→ The radical axis of two circles is defined to be the locus of a point which moves such that its powers with respect to the two given circles are equal.

→ The radical axis of two circles S = 0, S’ = 0 is

• the common chord when the two circles intersect at two distinct points.
• the common tangent at the point of contact when the circles touch each other.

→ The radical axis of any two circles bisects the line segment joining the points of contact of the common tangent of these two circles.

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Hyperbola Important Questions Short Answer Type

Question 1.
One focus of a hyperbola is located at the point (1, -3) and the corresponding directrix is the line y = 2. Find the equation of the hyperbola if its eccentricity is \(\frac{3}{2}\).
Solution:

Given that focus S = (1, -3)
The equation of the directrix is y – 2 = 0
Eccentricity e = \(\frac{3}{2}\)
Let P(x, y) be any point on the hyperbola.
Since P(x, y) lies on the hyperbola then SP
\(\frac{SP}{PM}\) = e
SP = e . PM
⇒ \(\sqrt{(x-1)^2+(y+3)^2}=\frac{3}{2}\left|\frac{0 \cdot x+y \cdot 1-2}{\sqrt{0^2+1^2}}\right|\)
⇒ \(\sqrt{(x-1)^2+(y+3)^2}=\frac{3}{2}|y-2|\)
Squaring on both sides
⇒ (x – 1)² + (y + 3)² = \(\frac{9}{4}\)(y – 2)²
⇒ x² + 1 – 2x + y² + 9 + 6y = \(\frac{9}{4}\)(y² + 4 – 4y)
⇒ 4x² + 4 – 8x + 4y² + 24y + 36 = 9y² – 36y + 36
⇒ 4x² – 5y² – 8x + 60y + 4 = 0
∴ The equation of the hyperbola is 4x² – 5y² – 8x + 60y + 4 = 0.

Question 2.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola x² – 4y² = 4. [(AP) Mar. ’20, ’18, ’16; May ’16; (TS) Mar. ’19]
Solution:
Given the equation of the hyperbola is x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{4 y^2}{4}=1\)
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
Here a = 2, b = 1
It is a hyperbola.
Centre = (0, 0)

Question 3.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 16y² – 9x² = 144. [(AP) Mar. ’18, May ’17]
Solution:
Given the equation of the hyperbola is 16y² – 9x² = 144
⇒ \(\frac{y^2}{9}-\frac{x^2}{16}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=-1\)
Here a = 4, b = 3
It is a conjugate hyperbola.
Centre C = (0, 0)

Question 4.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 5x² – 4y² + 20x + 8y = 4.
Solution:
Given equation of the hyperbola is 5x² – 4y² + 20x + 8y = 4
⇒ (5x² + 20x) + (-4y² + 8y) = 4
⇒ 5(x² + 4x) – 4(y² – 2y) = 4
⇒ 5(x² + 2 . 2x + 2² – 2²) – 4(y² – 2 . 1 . y + 1² – 1²) = 4
⇒ 5((x + 2)² – 4) – 4((y – 1)² – 1) = 4
⇒ 5(x + 2)² – 20 – 4(y – 1)² + 4 = 4
⇒ 5(x + 2)² – 4(y – 1)² = 20

we get h = -2; k = 1; a = 2; b = √3
It is a hyperbola.
Centre C = (h, k) = (-2, 1)

⇒ x = -2 ± \(\frac{4}{3}\)
⇒ 3x = -6 ± 4
⇒ 3x = -10 or 3x = -2
⇒ 3x + 10 = 0 or 3x + 2 = 0
The length of the latus rectum

Question 5.
If the line lx + my + n = 0 is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then show that a²l² – b²m² = n². (May ’07)
Solution:

Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let the line lx + my + n = 0 ………(1)
be a tangent to the given hyperbola at P(x₁, y₁)
∴ The equation of the tangent at P(x₁, y₁) is S₁ = 0
\(\frac{\mathrm{xx}_1}{\mathrm{a}^2}-\frac{\mathrm{yy}_1}{\mathrm{~b}^2}-1=0\)
Now (1) and (2) represent the same line.

Since P(x₁, y₁) lies on line (1) then
lx₁ + my₁ + n = 0
\(l\left(\frac{-\mathrm{a}^2 l}{\mathrm{n}}\right)+\mathrm{m}\left(\frac{\mathrm{b}^2 \mathrm{~m}}{\mathrm{n}}\right)+\mathrm{n}=0\)
⇒ -a²l² + b²m² + n² = 0
⇒ n² = a²l² – b²m²
⇒ a²l² – b²m² = n²

Question 6.
Find the equations of the tangents to the hyperbola x² – 4y² = 4 which are (i) parallel (ii) perpendicular to the line x + 2y = 0. [Mar. ’19 (AP) (TS) ’15 (TS); Mar. ’14; May ’14, ’13]
Solution:
Given the equation of the hyperbola is x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
Given the equation of the straight line is x + 2y = 0
(i) The equation of the tangent parallel to the line x + 2y = 0 is x + 2y + k = 0 ………(1)
2y = -x – k
y = \(\frac{-\mathrm{x}}{2}-\frac{\mathrm{k}}{2}\)
Comparing with y = mx + c,
we get m = \(\frac{-1}{2}\), c = \(\frac{-k}{2}\)
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ \(\left(\frac{-k}{2}\right)^2=4\left(\frac{-1}{2}\right)^2-1\)
⇒ \(\frac{k^2}{4}=\frac{4}{4}-1\)
⇒ k² = 0
⇒ k = 0
Substitute the value of k in equation (1)
x + 2y + 0 = 0
⇒ x + 2y = 0
∴ No parallel tangents to x + 2y = 0.
(ii) The equation of the tangent perpendicular to line x + 2y = 0 is
2x – y + k = 0
⇒ y = 2x + k ……..(2)
Comparing with y = mx + c,
we get m = 2, c = k.
Since equation (2) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ k² = 4(2)² – (1)² = 16 – 1
⇒ k² = 15
⇒ k = ±√15
Substitute the value of k in equation (2)
y = 2x ± √15
∴ The required perpendicular tangents are y = 2x ± √15

Question 7.
Find the equations of the tangents to the hyperbola 3x² – 4y² =12 which are (i) Parallel and (ii) Perpendicular to the line y = x – 7. [(TS) Mar. ’20, May ’18, ’15; (AP) Mar. ’17, ’15, May ’16, ’15]
Solution:
Given the equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
Here a² = 4, b² = 3
Given the equation of the straight line is y = x – 7
⇒ x – y – 7 = 0
(i) The equation of the tangent parallel to the line x – y – 7 = 0 is
x – y + k = 0 ………(i)
y = x + k
Comparing with y = mx + c,
we get m = 1, c = k
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ k² = 4(1)² – 3
⇒ k² = 1
⇒ k = ±1
Substitute the value of k in equation (1)
∴ The required parallel tangents are x – y ± 1 = 0
(ii) The equation of the tangent perpendicular to the line x – y – 7 = 0 is
x + y + k = 0 …….(2)
⇒ y = -x – k
Comparing with y = mx + c,
we get m = -1, c = -k
Since equation (2) is a tangent to the given hyperbola then
c² = a²m² – b²
(-k)² = 4(-1)² – 3
⇒ k² = 4 – 3
⇒ k² = 1
⇒ k = ±1
Substitute the value of k in equation (2)
∴ The required perpendicular tangents are x + y ± 1 = 0.

Question 8.
Find the equations of the tangents drawn to the hyperbola 2x² – 3y² = 6 through (-2, 1).
Solution:
Given the equation of the hyperbola is 2x² – 3y² = 6
⇒ \(\frac{x^2}{3}-\frac{y^2}{2}=1\)
Here a² = 3, b² = 2
Let, the given point P(x, y) = (-2, 1)
Let, the equation of the tangent to the hyperbola is
y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y = mx ± \(\sqrt{3 m^2-2}\) ……..(1)
Since, this tangent passes through the point P(-2, 1)
y = m(-2) ± \(\sqrt{3 m^2-2}\)
⇒ 1 = -2m ± \(\sqrt{3 m^2-2}\)
⇒ 1 + 2m = ±\(\sqrt{3 m^2-2}\)
Squaring on both sides
(1 + 2m)² = (±\(\sqrt{3 m^2-2}\))²
⇒ 1 + 4m² + 4m = 3m² – 2
⇒ m² + 4m + 3 = 0
⇒ m² + 3m + m + 3 = 0
⇒ m(m + 3) + 1(m + 3) = 0
⇒ (m + 3)(m + 1) = 0
⇒ m + 3 = 0 (or) m + 1 = 0
⇒ m = -3 (or) m = -1
Case (i): If m = -1, then the required tangents are from (1)
y = (-1)x ± \(\sqrt{3(-1)^2-2}\)
⇒ y = -x ± \(\sqrt{3-2}\)
⇒ y = -x ± 1
⇒ x + y ± 1 = 0
Since, the point (-2, 1) does not lie on the line x + y – 1 = 0
∴ The tangent is x + y + 1 = 0
Case (ii): If m = -3, then the required tangents are from (1)
y = (-3)x ± \(\sqrt{3(-3)^2-2}\)
⇒ y = -3x ± \(\sqrt{27-2}\)
⇒ y = -3x ± √25
⇒ 3x + y ± 5 = 0
Since, the point (-2, 1) does not lie on the line 3x + y – 5 = 0
∴ The tangent is 3x + y + 5 = 0
∴ Required tangents are x + y + 1 = 0, 3x + y + 5 = 0

Question 9.
Find the equation of the hyperbola whose asymptotes are the straight lines x + 2y + 3 = 0, 3x + 4y + 5 = 0, and which passes through the point (1, -1).
Solution:
Given that the asymptotes of a hyperbola are
x + 2y + 3 = 0 ……….(1)
3x + 4y + 5 = 0 ……….(2)
Let, the given point P = (1, -1)
The equation of the hyperbola whose asymptotes are the straight lines (1) & (2) is
(x + 2y + 3) (3x + 4y + 5) + k = 0 ……….(3)
Since equation (3) passes through the point P(1, -1) then
(1 + 2(-1) + 3) (3(1) + 4(-1) + 5) + k = 0
⇒ (1 – 2 + 3) (3 – 4 + 5) + k = 0
⇒ 8 + k = 0
⇒ k = -8
Substitute the value of ‘k’ in eq. (3)
∴ The required equation of the hyperbola is (x + 2y + 3) (3x + 4y + 5) – 8 = 0
⇒ 3x² + 4xy + 5x + 6xy + 8y² + 10y + 9x + 12y + 15 – 8 = 0
⇒ 3x² + 10xy + 8y² + 14x + 22y + 7 = 0

Question 10.
Prove that the product of the perpendicular distances from any point on a hyperbola to its asymptotes is constant.
Solution:
Let S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0 be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equations of asymptotes of hyperbola S = 0 are \(\frac{x}{a}+\frac{y}{b}=0\) and \(\frac{x}{a}-\frac{y}{b}=0\)
⇒ bx + ay = 0 ……..(1)
and bx – ay = 0 ……… (2)
Let PM be the length of the perpendicular drawn from P(a sec θ, b tan θ) on line (1).
∴ PM = \(\frac{|b a \sec \theta+a b \tan \theta|}{\sqrt{a^2+b^2}}\)
Let PN be the length of the perpendicular drawn from P (a sec θ, b tan θ) on line (2).


∴ The product of the perpendicular distances from any point on a hyperbola to its asymptotes is a constant.

Question 11.
Find the centre, foci, eccentricity, equation of the directrices, and length of the latus rectum of the hyperbola 9x² – 16y² + 72x – 32y – 16 = 0. (May ’01)
Solution:
Given equation of the hyperbola is 9x² – 16y² + 72x – 32y -16 = 0
⇒ (9x² + 72x) +(-16y² – 32y) = 16
⇒ 9(x² + 8x) – 16 (y² + 2y) = 16
⇒ 9(x² + 2 . 4 . x + 4² – 4²) – 16(y² + 2 . 1 . y + 1² – 1²) = 16
⇒ 9((x + 4)² – 16) – 16((y + 1)² – 1) = 16
⇒ 9(x + 4)² – 144 – 16(y + 1)² + 16 = 16
⇒ 9(x + 4)² – 16(y + 1)² = 144

we get h = -4, k = -1, a = 4, b = 3.
It is a hyperbola.
Centre C = (h, k) = (-4, -1)

x = -4 ± \(\frac{16}{5}\)
5x = -20 + 16 or 5x = – 20 – 16
5k = -4 or 5x = -36
5x + 4 = 0 or 5x + 36 = 0
Length of latus rectum = \(\frac{2 \mathrm{~b}^2}{\mathrm{a}}=\frac{9}{2}\)

Question 12.
Find the centre, eccentricity, foci, directrices, and the length of the latus rectum of the hyperbola 4x² – 9y² – 8x – 32 = 0.
Solution:
Given equation of the hyperbola is 4x² – 9y² – 8x – 32 = 0
⇒ (4x² – 8x) + (-9y²) = 32
⇒ 4(x² – 2x) – 9y² = 32
⇒ 4((x)² – 2 . 1 . x + 1² – 1²) – 9y² = 32
⇒ 4((x – 1)² – 1) – 9y² = 32
⇒ 4(x – 1)² – 4 – 9y² = 32
⇒ 4(x – 1)² – 9y² = 36

we get a = 3, b = 2, h = 1, k = 0
It is a hyperbola.
Centre C(h, k) = (1, 0)

Question 13.
Tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) make angles θ₁, θ₂ with transverse axis of a hyperbola. Show that the point of intersection of these tangents lies on the curve 2xy = k(x² – a²), when tan θ₁ + tan θ₂ = k. [(TS) May ’19, ’16; (AP) May ’18]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let P(x₁, y₁) be the point of intersection of the tangents

Question 14.
Prove that the point of intersection of two perpendicular tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) lies on the circle x² + y² = a² – b². [(TS) May ’17; Mar. ’16]
Solution:
Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Equation of any tangent to the hyperbola is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
Suppose P(x₁, y₁) is the point of intersection of a tangent.
Since P lies on the tangent then
y₁ = mx₁ ± \(\sqrt{a^2 m^2-b^2}\)
y₁ – mx₁ = ±\(\sqrt{a^2 m^2-b^2}\)
Squaring on both sides

This is a quadratic equation in m given the values for m say m₁ and m₂.
The tangents are perpendicular then m₁m₂ = -1

∴ P(x₁, y₁) lies on the circle x² + y² = a² – b²

Question 15.
Show that the locus of feet of the ⊥ars drawn from foci to any tangent of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is the auxiliary circle of the hyperbola.
Solution:

Let the equation of hyperbola be
S = \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\)
Let P(x₁, y₁) be the foot of the ⊥ar drawn from either of the foci to a tangent.
The equation of the tangent to the hyperbola S = 0 is
y = mx ± \(\sqrt{a^2 m^2-b^2}\) …….(1)
The equation to the ⊥ar from either focus (±ae, 0) on this tangent is
y – y₁ = \(\frac{1}{m}\)(x – x₁)


∴ P lies on x² + y² = a² which is a circle with the centre as the origin, the centre of the hyperbola.

Question 16.
Find the centre, eccentricity, foci, length of latus rectum, and equations of the directrices of the hyperbola 4(y + 3)² – 9(x – 2)² = 1. [(AP) May ’19]
Solution:
Given hyperbola is 4(y + 3)² – 9(x – 2)² = 1
⇒ \(\frac{(y+3)^2}{\frac{1}{4}}-\frac{(x-2)^2}{\frac{1}{9}}=1\)

Question 17.
Show that the equation of a hyperbola in the standard form is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). [May ’02, ’99, ’98]
Solution:
Proof: Let ‘S’ be the focus, ‘e’ be the eccentricity and L = 0 be the directrix of the hyperbola.

Let ‘P’ be a point on the hyperbola.
Let MZ be the projection of PS on the directrix L = 0 respectively.
Let ‘N’ be the projection of ‘P’ on SZ.
Since e > 1 we can divide SZ both internally and externally in the ratio e : 1.
Let A, A’ be the points of division of ‘SZ’ in the ratio e : 1 internally and externally respectively.
Let AA’ = 2a.
Let ‘C’ be the midpoint of AA’.
Points A, A’ lies on the hyperbola then
\(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
Now \(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{e}}{1}\)
SA = e AZ
CS – CA = e (CA – CZ) ……..(1)
and \(\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
SA’ = eZA’
CS + CA’ = e (CZ + CA’) ……….(2)
Now (1) + (2),
(CS – CA) + (CS + CA’) = e (CA – CZ) + e(CA’ + CZ)
CS – CA + CS + CA’ = e (CA – CZ + CZ + CA’)
2CS – CA + CA’ = e (CA + CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
2CS – CA + CA = e (CA + CA)
2CS = 2eCA
CS = e CA
CS = ae (∵ CA = a)
∴ The coordinates of focus S = (ae, 0)
Now (1) – (2),
(CS – CA) – (CS + CA’) = e(CA – CZ) – e(CA’ + CZ)
CS – CA – CS – CA’ = e(CA – CZ – CA’ – CZ) – CA – CA’ = e (CA – 2CZ – CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
-CA – CA = e(CA – 2CZ – CA)
– 2CA = -2e CZ
CA = e CZ
a = e CZ
CZ = \(\frac{a}{e}\)
∴ The equation of the directrix is x = \(\frac{a}{e}\).
Take CS, the principal axis of the hyperbola as the X-axis, and CY ⊥ CS as Y-axis.
Then S = (ae, 0) and the hyperbola is in the standard form.
Let P = (x, y)
Now, PM = ZN = CN – CZ = x – \(\frac{a}{e}\)
P lies on the hyperbola
\(\frac{SP}{PM}\) = e
SP = e PM
\(\sqrt{(x-a e)^2+(y-0)^2}=e\left(x-\frac{a}{e}\right)\)
Squaring on both sides
(x – ae)² + y² = \(\mathrm{e}^2\left(\mathrm{x}-\frac{\mathrm{a}}{\mathrm{e}}\right)^2\)

where b² = a²(e² – 1) > 0
The locus of ‘P’ is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
∴ The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

Question 18.
Show that the difference in focal distances of any point on the hyperbola is constant
(or)
The difference of the focal distances of any point on the hyperbola is constant i.e. if ‘P’ is a point on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) with foci S and S’ then S’P – SP = 2a.
Solution:

Let P (x, y) be any point on the hyperbola whose centre is the origin ‘C’.
Foci are S, S’
Directrices of ZM and Z’M’.
Let PN, PM, PM’ be the perpendiculars drawn from ‘P’ upon X-axis and the two directrices respectively.
Now, \(\frac{SP}{PM}\) = e
SP = e PM
= e ZN
= e (CN – CZ)
= e (x – \(\frac{a}{e}\))
Also = \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}=\mathrm{e}\)
S’P = ePM’
= eNZ’
= e (CN + CZ’)
= e (x + \(\frac{a}{e}\))
LHS = S’P – SP
= \(e\left(x+\frac{a}{e}\right)-e\left(x-\frac{a}{e}\right)\)
= ex + a – ex + a
= 2a (constant)
∴ S’P – SP = 2a

Question 19.
Show that the condition for straight line y = mx + c to be a tangent to the hyperbola S = 0 is c² = a²m² – b². [Mar. ’03]
Solution:
Suppose y = mx + c ………(1) is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at P is
\(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}-1=0\) ……..(2)
Now (1) and (2) represent the same line

Question 20.
Show that the equation of the normal at P(θ) on the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b². [Mar. ’06]
Solution:
The equation of the tangent at P(θ) is \(\frac{x \sec \theta}{a}-\frac{y \tan \theta}{b}=1\)
Slope of tangent = \(\frac{\frac{-\sec \theta}{a}}{\frac{-\tan \theta}{b}}=\frac{b \sec \theta}{a \tan \theta}\)
Slope of normal = \(-\frac{a \tan \theta}{b \sec \theta}\)
∴ The equation of the normal at P is
y – b tan θ = \(-\frac{a \tan \theta}{b \sec \theta}\) (x – a sec θ)
⇒ by sec θ – b² sec θ tan θ = -ax tan θ + a² sec θ tan θ
⇒ ax tan θ + by sec θ = (a² + b²) sec θ tan θ
⇒ \(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}=a^2+b^2\)

Question 21.
If the line lx + my = 1 is a normal to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), then show that \(\frac{a^2}{l^2}-\frac{b^2}{m^2}=\left(a^2+b^2\right)^2\).
Solution:

Given equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Let the line lx + my – 1 = 0 ……….(1) be normal to the given hyperbola at P(θ).
The equation of normal at P(θ) to the given hyperbola is
\(\frac{a x}{\sec \theta}+\frac{b y}{\tan \theta}\) = a² + b² …….(2)
Now (1) & (2) represent the same line.

which is the required condition.

Question 22.
Show that the equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents
(i) an ellipse if ‘c’ is a real constant less than 5.
(i) a hyperbola if ‘c’ is any real constant between 5 and 9.
(iii) Show that each ellipse in (a) and each hyperbola in (b) has foci at the two points (±2, 0), independent of the value ‘c’.
Solution:
(i) Given equation is \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\)
This equation represents an ellipse if
9 – c > 0 and 5 – c > 0
9 > c and 5 > c
c < 9 and c < 5
∴ c < 5
(ii) Given equation is \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\)
This equation represents a hyperbola if
9 – c > 0 and 5 – c < 0
9 > 0 and 5 < c
c < 9 and c > 5
∴ 5 < c < 9
(iii) In case (i): a² = 9 – c, b² = 5 – c
Now, a² – b² = (9 – c) – (5 – c)
⇒ a² – a²(1 – e²) = 9 – c – 5 + c
⇒ a²e² = 9 – 5
⇒ a²e² = 4
⇒ ae = 2
∴ foci are (±ae, 0) = (±2, 0)
In case (ii): a² = 9 – c, b² = c – 5
Now, a² + b² = 9 – c + c – 5
⇒ a² + a²(e² – 1) = 9 – 5
⇒ a²e² = 4
⇒ ae = 2
∴ foci are (±ae, 0) = (±2, 0)
These are independent of the value of ‘c’

Question 23.
A circle cuts the rectangular hyperbola xy = 1, in the points (x₁, y₁), r = 1, 2, 3, 4. Prove that x₁x₂x₃x₄ = y₁y₂y₃y₄ = 1.
Solution:
Let the circle be x² + y² = a²
Since (t, \(\frac{1}{2}\)) (t ≠ 0) lies on xy = 1
The points of intersection of the circle and the hyperbola are given by
\(t^2+\frac{1}{t^2}=a^2\)
⇒ t⁴ – a²t² + 1 = 0
⇒ t⁴ + 0 . t³ – a²t + 0 . t + 1 = 0
If t₁, t₂, t₃, t₄ are the roots of the above biquadratic, then
product of the roots t₁t₂t₃t₄ = \(\frac{1}{1}\) = 1

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 6 Binomial Theorem will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Binomial Theorem Formulas

→ If a, x are real numbers and n is a positive integer, then

• (x + a)ⁿ = ⁿC₀ xⁿ. a⁰ + ⁿC₁. x^n-1 . a¹ + ⁿC₂. x^n-2. a² + ………… + ⁿC_r. x^n-r. a^r + ……………. + (-1)^{r n}C_n. x⁰ . aⁿ
• (x – a)ⁿ = ⁿC₀ xⁿ. a⁰ – ⁿC₁. x^n-1 . a¹ + ⁿC₂. x^n-2. a² + ………… + ⁿC_r. x^n-r. a^r + ……………. + (-1)^{r n}C_n. x⁰ . aⁿ

→ Each of the above two expansions contain (n + 1) terms in R.H.S.

→ The general term of (x + a)ⁿ is T_r+1 = ⁿC_r x^n-r . a^r (0 ≤ r ≤ n)

→ If n is fixed we write ⁿC_r = C_r and C₀, C₁ C₂ ………….. C_n are called the binomial coefficients.

• C₀ + C₁ + C₂ …………….. + C_n = 2ⁿ
• C₀ – C₁ + C₂ – C₃ + ……………. + (-1)ⁿC_n = 0
• C₀ + C₂ + C₄ + ………….. = C₁ + C₃ + C₅ + …………… = 2^n-1

→ \(\sum_{r=0}^n\)C_r = 2ⁿ
\(\sum_{r=1}^n\)r. C_r = n. 2^n-1
\(\sum_{r=2}^n\) r(r – 1). C_r = n(n – 1).2^n-2
\(\sum_{r=1}^n\) r² .C_r = n(n + 1) 2^n-2

→ (i) If n is even then the expansion of (x + a)ⁿ has only one middle term. It is
T_{\(\frac{n}{2}\)+1} = ⁿC_{\(\frac{n}{2}\)} . x^{\(\frac{n}{2}\)}. a^{\(\frac{n}{2}\)}

(ii) If n is odd, then the expansion of (x + a)ⁿ has two middle terms. They are
T_{\(\frac{n+1}{2}\)} = nC_{\(\left(\frac{n-1}{2}\right)\)} . x^{\(\frac{n+1}{2}\)}. a^{\(\frac{n-1}{2}\)} and T_{\(\frac{n+3}{2}\)} = nC_{\(\left(\frac{n+1}{2}\right)\)} . x^{\(\frac{n-1}{2}\)} . a^{\(\frac{n+1}{2}\)}

→ Numerically greatest term in the expansion of (1 + x)” :

• If \(\frac{(\mathrm{n}+1)|\mathrm{x}|}{1+|\mathrm{x}|}\) is not an integer and if its integral part \(\left[\frac{(n+1)|x|}{1+|x|}\right]\) = r, a positive integer then T_r+1 is the numerically greatest term in the expansion of (i + x)ⁿ.
• If \(\frac{(n+1)|x|}{1+|x|}\) is positive integer, say m, then |T_m| = |T_m+1| and hence T_m and T_m+1 both are numerically greatest terms in the expansion of (1 + x)ⁿ.

→ If x is a real number such that |x| < 1 and p. q are positive integers, then

→ If n is a positive integer and x is a real number such that j x j < 1, then

• If |x| is so small that x² and higher powers of x may be neglected, then (1 + x)ⁿ = 1 + nx.
• If |x| is so small that x³ and higher powers of x may be neglected, then
  (1 + x)ⁿ = 1 + nx + \(\frac{n(n-1)}{2 !}\)x².
• if |x| is so small that x⁴ and higher powers of x may be neglected, then
  (1 + x)ⁿ = 1 + nx + \(\frac{n(n-1)}{2 !}\)x² + \(\frac{n(n-1)(n-2)}{3 !}\)x³

→ (1 + x)^p/q = 1 + \(\frac{\frac{p}{q}}{1 !}\)x + \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right)}{2 !}\)x² + \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right)\left(\frac{p}{q}-2\right)}{3 !}\)x³ + ……. + \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right) \cdots\left(\frac{p}{q}-r+1\right)}{r !}\).x^r + …………
T_r+1 = \(\frac{\frac{p}{q}\left(\frac{p}{q}-1\right)\left(\frac{p}{q}-2\right) \ldots \ldots\left(\frac{p}{q}-r+1\right)}{r !}\). x^r for r ∈ N.

→ Let n ∈ N and a, b, c ∈ R, then (a + b + c)ⁿ contains \(\frac{(\mathrm{n}+1)(\mathrm{n}+2)}{2}\) terms.
Also (a +b + c)ⁿ = \(\sum_{{0 \leq p, q, r \leq n \\ p+q+r=n}} \frac{n !}{p ! q ! r !}\) a^p . b^q. c^r