TS Inter 2nd Year Chemistry Study Material Chapter 1 Solid State

Telangana TSBIE TS Inter 2nd Year Chemistry Study Material 1st Lesson Solid State Textbook Questions and Answers.

TS Inter 2nd Year Chemistry Study Material 1st Lesson Solid State

Very Short Answer Questions (2 Marks)

Question 1.
Define the term ‘amorphous’. Give a few examples of amorphous solids.
Answer:
An amorphous solid is a substance whose constituent particles do not possess a regular orderly arrangement. Ex : Glass, plastics, rubber, starch etc.

Question 2.
What makes a glass different from a solid such as quartz?
Answer:
Glass is an amorphous form of silica and do not posses long range regular structure. It do not posses sharp melting point.

Quartz is a crystalline form of silica and have long range regular structure. It has sharp melting point. If the molten quartz Is cooled rapidly it becomes glass.

Question 3.
Classify each of the following solids as ionic, metallic, molecular, network (covalent) or amorphous.
a) Tetra phosphorous deoxide
b) Graphite
c) Brass
d) Ammonium phosphate (NH₄)₃ PO₄
e) SIC
f) Rb
g) I₂
h) LiBr
i) P₄
j) Si
k) plastic.
Answer:

Question 4.
What is meant by the term coordination number?
Answer:
The number of nearest neighbours of a particle in a packing is called coordination number, eg : in hexagonal close packing coordination number is 12.

Question 5.
What is the coordination number of atoms in cubic close – pack structure ?
Answer:
In cubic close – packed structure coordi-nation number is 12.

Question 6.
What is the coordination number of atoms in a body – centered cubic structure ?
Answer:
In a body centred cubic structure coordi-nation number is 8.

Question 7.
Stability of a crystal is reflected in the magnitude of Its melting point. Comment.
Answer:
If the interparticle forces are stronger more energy is required to separate them. The crystals in which jilter particle forces are stronger are stable. More stable crystals have higher melting points than less stable crystals. Hence we can say that stability of a crystal is reflected in magnitude of its melting point.

Question 8.
How are the intermolecular forces among the molecules affect the melting point ?
Answer:
If the intermolecular forces among the molecules are stronger, more energy is required to separate them. Such solids require more amount of energy to melt. Hence they have higher melting points. If the intermolecular forces are weak, less energy is sufficient to melt them. Such solids have low melting points.

Question 9.
How do you distinguish between hexagonal close packing and cubic close packing structures ?
Answer:
In hexagonal close – packing every third layer is similar to the first layer. Thus there is ABABAB ………. arrangement. In cubic close packing every fourth layer is similar to first, there is ABC ABC…. arrangement.

Question 10.
How do you distinguish between crystal lattice and unit cell ?
Answer:
A crystal lattice may be defined as a regular three dimensional arrangement of identical points in space.
A unit cell may be defined as a three dimensional group of lattice points that generates the whole lattice by translation or stacking. It is the smallest repetitive portion of the crystal lattice.

Question 11.
How many lattice points are there in one unit cell of face – centered cubic lattice ?
Answer:
A face centred cubic unit cell has lattice points at the corners of the cube and at face centres. So it contain 8 + 6 = 14 lattice points.

Question 12.
How many lattice points are there in one unit cell of face centered tetragonal lattice ?
Answer:
A face centred tetragonal unit cell has 4 atoms per unit cell.

Question 13.
How many lattice points are there in one unit cell of body centered cubic lattice ?
Answer:
A body centred cubic unit cell has lattice points at the corners of the cube and at the body centre. So the total number of lattice points in one unit cell of a body centred cubic lattice is 9.

Question 14.
What is a semiconductor ?
Answer:
Semiconductors are solids with conductivi-ties in the intermediate range from 10^-6 to 10⁴ ohm^-1 m^-1. Their conductivity increases with increase in temperature.

Question 15.
What is Schottky defect ? (AP & TS ’15)
Answer:
The Schottky defect is simply a vacancy defect in ionic solids. This is due to missing of equal number of positive and negative ions. It is more common in ionic compounds

with high coordination number and in the ionic scJlids which contain positive and negative ions of equal size. This defect decreases density of the substance, eg. NaCl, KCl, CsCl, AgBr.

Question 16.
What is Frenkel defect ? (AP & TS ’15) (Mar. 2018 . TS)
Answer:
Frenkel defect arises when the smaller ion of ionic solids is dislocated from its normal site to an interstitial site. Frenkel defects

are common in ionic solids having low coordination number and large difference in the sizes of positive and negative ions. The density of the substance do not change, eg. ZnS, AgCl, AgBr and Agl.

Question 17.
What is interstitial defect ?
Answer:
If the constituent particles of a solid occupies the interstitial sites instead of lattice points, it is called interstitial defect. It is observed in non – ionic solids.

Question 18.
What are F – centres ?
Answer:
A compound may have excess metal ion if a negative ion is absent from its lattice site, leaving a hole which is occupied by electron to maintain electrical neutrality. The holes occupied by electrons are called F – centres.

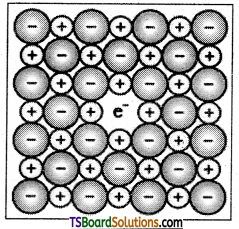
Question 19.
Explain ferromagnetism with suitable example.
Answer:
The substances which are strongly attracted by external magnetic field are called ferromagnetic substances. They contain unpaired electrons, eg. iron, cobalt, nickel.

Question 20.
Explain paramagnetism with suitable example.
Answer:
Substances which are weakly attracted by a magnetic field are called paramagnetic substances. This is due to the presence of one or more unpaired electrons. Ex : O₂, Cu⁺², Fe⁺³, Cr⁺³ etc.

Question 21.
Explain Ferromagnetism with suitable example.
Answer:
When the magnetic moments of the domains in a substance are aligned in parallel and anti parallel directions in unequal numbers, then they are said to exhibit Fern magnetism. They are weakly attracted by magnetic field.
Eg: Fe₃O₄, MgFe₂O₄, NiFe₂O₄ etc.

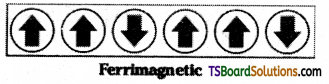
Question 22.
Explain Antiferro magnetism with suitable example.
Answer:
When the magnetic moments of the domain in a substance are aligned in opposite directions and cancel out each others moment, then they are said to exhibit Anti ferromagnetism.

Question 23.
Why x-ray are needed to probe the crystal structures ?
Answer:
According to a fundamental principle of optics, the wavelength of light used to observe an object must be no greater than twice the length of the object itself. Since atoms have diameters of around 2 × 10^-10 m and the visible light detected by our eyes has wavelength of 4 – 7 × 10^-7 m, it is impossible to see atoms using even the tinest optical microscope. Hence, to see atoms we must use light wdth a wave length of approximately 10^-10 m, which is in the x – ray region of electromagnetic spectrum.

Short Answer Questions (4 Marks)

Question 24.
Explain similarities and differences between metallic and ionic crystals.
Answer:
Similarities:

1. In metallic and Ionic solids the constituent particles are in regular arrangement. So both have a regular shape.
2. In both solids the bond is non – directional.
3. Both solids are hard.

Differences:

1. In metallic crystals the constituent particles are positive ions immersed in sea of mobile electrons but in ionic solids the constituent particles are positive and negative ions.
2. In metallic crystals binding force is metallic bond whereas in ionic crystals is ionic bond.
3. Metallic crystals are conductors of electricity while ionic crystals are insulators in solid state and act as conductors in molten state and aqueous solutions.
4. Metallic crystals are malleable and ductile while ionic crystals are brittle.

Question 25.
Explain why ionic solids are hard and brittle.
Answer:
Ionic solids are hard because in ionic solids, ions are held together by strong electrostatic attractive forces. If sufficient force is applied on ionic crystals, the ions with similar charges come close due to displacement. Thus the crystal breaks due to repulsions between similar charges.
Hence Ionic solids are brittle.

Question 26.
Calculate the efficiency of packing In case of a metal of simple cubic crystal.
Answer:
Packing efficiency in simple cubic lattice:
In a simple cubic lattice the atoms are located only on the corners of the cube. The particles touch each other along the edge.
Thus, the edge length or šide of the cube
‘a’, and the radius of each particle, r are related as a = 2r

Simple cubic unit cell. The spheres are in contact with each other along the edge of the cube.
The volume of the cubic unit cell = a³
= (2r)³ = 8r³
Since a simple cubic unit cell contains only 1 atom.
The volume of the occupied space = \(\frac{4}{3} \pi r^3\)
Packing efficiency

Question 27.
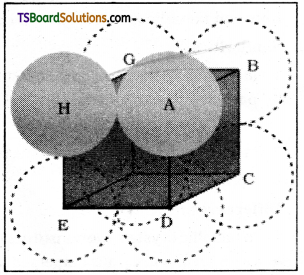
Calculate the efficiency of packing in case of a metal of body – centred cubic crystal.
Answer:
From Fig it is clear that the atom at the centre will be in touch with the other two atoms diagonally arranged.
In ΔEFD
b² = a² + a² = 2a²
b = \(\sqrt{2} a\)
Now in ΔAFD
c² = a² + b² = a² + 2a² = 3a²
c = \(\sqrt{3} a\)

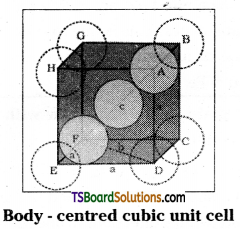
(sphere along the body diagonal are shown with solid boundaries).
The length of the body diagonal c is equal to 4r.

where r is the radius of the sphere (atom), as all the three špheres along the diagonal touch each other.
Therefore, \(\sqrt{3} a\) = 4r = a = \(\frac{4 r}{\sqrt{3}}\)
Also we can write, r = \(\frac{\sqrt{3}}{4} a\)
In this type of structure, total number of atoms is 2 and their volume is 2 × \(\left(\frac{4}{3}\right) \pi r^3\)
Volume of the cube, a³ will be equal to
\(\left(\frac{4}{\sqrt{3}} \mathrm{r}\right)^3\) or a³ = \(\left(\frac{4}{\sqrt{3}} \mathrm{r}\right)^3\)
Therefore
Packing efficiency

Question 28.
Calculate the efficiency of packing in case of face – centered cubic crystal.
Answer:
Both types of close packing (hep and ccp) are equally efficient. Let us calculate the efficiency of packing in ccp structure. In Fig. let the unit cell edge length be a’ and face diagonal AC = b.
In Δ ABC
AC² = b² = BC² + AB² = a² + a² = 2a² (or)
b = \(\sqrt{2}\)
If r is the radius of the sphere, we find b = 4r = \(\sqrt{2 a}\) (or) a = \(\frac{4 r}{\sqrt{2}}\) = \(2 \sqrt{2 r}\)
(we can also write, r = \(\frac{a}{2 \sqrt{2}}\))

Cubic close packing other sides are not provided with spheres for sake of clarity

We know, that each unit cell in ccp structure, has effectively 4 spheres. Total volume of four spheres is equal to 4 × (4/3) πr³ and volume of the cube is a³ or \((2 \sqrt{2} r)^3\).
Therefore,
Packing efficiency
Volume occupied by four spheres

The same packing efficiency occurs in hep arrangement also.

Question 29.
A cubic solid is made of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body – centre. What is the formula of the compound ? What are the coordination numbers of P and Q ?
Answer:
The atom at corner makes \(\frac{1}{8}\) contribution while atom at body centre makes 1 contri-bution to the unit cell.
No. of atoms of Q per unit cell
= 8 (at corners) × \(\frac{1}{8}\) = 1
No. of atoms of P per unit cell
= 1 (at body centre) × 1 = 1
∴ Formula of the compound is PQ.
The atom at the body centre would be in contact with all the atoms at the corners. Hence the coordination number of P would be 8. Similarly coordination number of Q is also 8.

Question 30.
If the radius of the octahedral void is ‘r’ and radius of the atoms in close packing is ‘R’, derive relation between r and R.
Answer:
The octahedral void can be represented as follows.

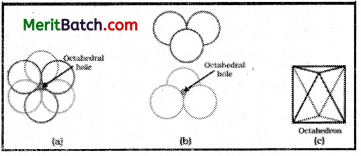
Though an octahedral void is surrounded by six spheres only four are shown in the figure. The spheres present above and below the void are omitted.
Let the length of one side of the square ABCD is a cm.
In right angled ΔABC,
The diagonal AC
= \(\sqrt{\mathrm{AB}^2+\mathrm{BC}^2}\) = \(\sqrt{a^2+a^2}\) = \(\sqrt{2} a\)
But AC = 2R + 2r ∴ 2R + 2r = \(\sqrt{2} a\)
But a = 2R ∴ 2R + 2r = \(\sqrt{2} .2 \mathrm{R}\)
Dividing by 2R we get 1 + \(\frac{r}{R}\) = \(\sqrt{2}\)
\(\frac{r}{R}\) = \(\sqrt{2}\) – 1 = 1.414 – 1 = 0.414

Question 31.
Describe the two main types of semiconductors and contrast their conduction mechanism. (Mar. ’19, ’18. AP)
Answer:
Semiconductors are o two types. They are
1) Intrinsic semiconductors
2) Extrinsic semiconductors.

1) Intrinsic semiconductors: In this type of semiconductors, electrical conductivity increases with rise in temperature, since more electrons can jump to conduction band. Eg :Silicon and Germanium.

2) Extrinsic semiconductors: In this type of semiconductors, conductivity is increased by adding a appropriate amount of suitable impurity. This process is called Doping. Doping can be done with an impurity which is electron rich or electron deficient. These are of two types.

a) n – type semiconductors : The semi-conductors in which the increase in conductivity is due to the negatively charged electron are called n-type semiconductors.
Eg : Silicon and germanium of group 14 doped with a group 15 elements like P or As form n – type semiconductors.

b) p – type semiconductors : The semi-conductors in which the increase in conductivity is due to the positively charged holes are called p – type semi-conductors.
Ex : Silicon or germanium can also be doped with group B elements like B, Al or Ga from p-type semiconductors.

Question 32.
Classify each of the following as either a p – type or a n – type semiconductor.
1) Ge doped with In
2) Si doped with B.
Answer:
1) Ge is an element of group -14. Its outer electronic configuration is 4s² 4p². When it is doped with In group – 13 element having 5s² 5p¹ configuration it can form three covalent bonds with germanium. The fourth bond of germanium contains only one electron and hence it is an electron deficient bond or a hole is created. Conductivity is due to these holes. Therefore it is a p – type semiconductor.

2) Silicon is an element of group -14 with an outer electron configuration 2s² 2p². When it is doped with Boron, an element of group -13 with 3s² 3p¹ configuration, it can form three covalent bonds with silicon. The fourth bond of silicon contain only one electron and hence it is an electron deficient bond or a hole is created. Conductivity is due to these holes. Therefore it is a p – type semi-conductor.

Question 33.
Analysis shows that nickel oxide has the formula Ni_0.98O_1.00. What fractions of nickel exist as Ni²⁺ and Ni³⁺ ions ?
Answer:
From the given formula it is clear that for every 100 oxide ions there are only 98 nickel ions. Suppose, out of 98 nickel ions x exist as Ni²⁺ and the remaining (98 – x) exist as Ni³⁺
Total positive charge on 98 nickel ions = x × 2 + (98 – x) 3
Total negative charge on 100 oxide ions
= 100 × 2 = 200
Due to electrical neutrality,
x × 2 + (98 – x)3 = 200
2x + 294 – 3x = 200
x = 94
∴ Fraction of nickel as Ni²⁺ = \(\frac{94}{98}\) × 100
= 96%
Fraction of nickel as Ni³⁺ = (100 – 96)% = 4%

Question 34.
Gold (atomic radius = 0.144nin) crystallizes in a face centred unit cell. What is the length of a side of the unit cell?
Answer:
Radius of gold atom r = 0.144 nm
In face centred unit cell, lace diagonal
= 4r = \(\sqrt{2} a\)
∴ a = \(\frac{4 \mathrm{r}}{\sqrt{2}}\) = \(2 \sqrt{2}\) × r = 2 × 1.414 × 0.144mn
= 0.407 nm
Edge length of unit cell, a = 0.407 nm

Question 35.
In terms of band theory, what is the difference between a conductor and an insulator?
Answer:
In a metal the outer orbitals of very large number of atoms overlap to form a very large number of molecular orbitals that are delocalised over the metal. As a result a large number of energy levels are crowded together into bands. The highest occupied energy band is called the valence band while the lowest unoccupied energy band is called conduction band. The energy difference separating the valence band and conduction band is called band gap or energy gap.

In conductors the valence band is only partially filled. So electrons may easily excited from lower energy level to higher energy level by supplying a very small amount of energy. When a voltage is applied to a metal crystal, electrons are excited to the unoccupied orbitals in the same band and move towards the positive terminal. Thus, a material with partly filled energy band is a conductor.

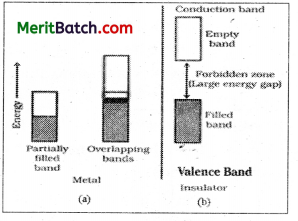
In case of insulators, the highest occupied band is completely filled. The energy gap between the fully filled valence band and the vacant conduction band is very large and it is not possible to excite the electrons to the conduction band. So they become insulators.

Question 36.
In terms of band theory, what is the’ difference between a conductor and a semiconductor?
Answer:
In a metal the outer orbitals of very large number of atoms overlap to form a very large number of molecular orbitals that are delocalised over the metal. As a result a large number of energy levels are crowded together into bauds. The highest occupied energy band is called the valence hand while the lowest unoccupied energy band is called conduction band. The energy difference separating the valence band and conduction band is called band gap or energy gap.

In conductors the valence band is only partially filled. So electrons may easily excited from lower energy level to higher energy level by supplying a very small amount of energy. When a voltage is applied to a metal crystal, electrons are excited to the unoccupied orbitals in the same band and move towards the positive terminal. Thus, a material with partly filled energy band is a conductor.

In the case of semiconductors, the forbidden band i.e., the energy gap bet-ween valence band and conduction band is little. The thermal energy available at room temperature is enough to excite some electrons from the highest occupied band to the next permitted energy band. So conductivity occurs but their conductivity is in between the conductors and insulators.

Question 37.
If NaCl is doped with 1 × 10^-3mol percent of SrCl₂, what is the concentration of cation vacancies?
Answer:
Every Sr²⁺ ion causes one cation vacancy (because two Na⁺ ions are replaced by one Sr²⁺).
Therefore, introduction of 10^-3 moles of SrCl₂ per 100 moles of NaCl would introduce 10^-3 mole cation vacancies in 100 moles of NaCl.
No. of vacancies per mole of NaCl
= \(\frac{10^{-3}}{100}\) × 6.02 × 10²³
= 6.02 × 10¹⁸ vacancies mol^-1.

Question 38.
Derive Bragg’s equation. (TS Mar. 19) (AP 17, 16, 15; TS 16, 15; IPE 14)
Answer:
When a beam of X – rays strikes a crystal, the constituent particles of the crystal scatter or deflect some of the X – rays from their original path. The scattered X – rays can be detected on a photographic plate. From the diffraction pattern, the distance between constituent particles in a crystal can be studied.

In the above figure X – rays with wave-length λ strike a crystal face at an angle θ and then reflect at the same angle. The rays that strike an atom in the second layer are diffracted at the same angle θ, but because the second layer of atoms away from the X – ray source, the distance that the X – rays has to travel is more to reach the second layer. The path difference is indicated by AB in the figure. AB is equal to the distance between atomic layers d(=zB) times the sine of the angle θ.

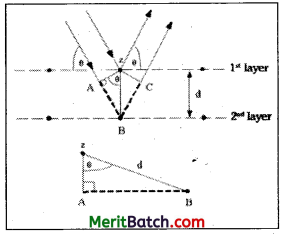
sin θ = \(\frac{\mathrm{AB}}{\mathrm{d}}\) ; so AB = d sin θ
The X – rays have to travel a total extra distance AB + BC.
AB + BC = 2d sin θ (∴ AB = BC)
The different X – rays striking the two layers of atoms are in – phase initially and also they will be in – phase after reflection only the extra distance AB + BC is equal to a whole number of wavelengths nX where n is an integer (1, 2, 3, 4….)
∴ AB + BC = 2d sin θ = nλ
This is known as Bragg’s equation.
By knowing the value of φ, λ the value of θ can be measured, and the value of n is a small integer, usually 1. Thus the distance d between layers of atoms in a crystal can be calculated.

Long Answer Questions (8 Marks)

Question 39.
How do you determine the atomic mass of an unknown metal if you know its density and dimension of its unit cell ? Explain.
Answer:
From the dimensions of the unit cell, it is possible to calculate the volume of the unit cell. From the knowledge of the density of unit cell we can calculate the mass of atoms in the unit cell or vice versa.
If we know the edge length of a cubic crystal of an element or compound, we can easily calculate its density as described below.

Consider a unit cell of edge ‘a’ picometer (pm)
The length of the edge of the cell = a pm
= a × 10^-12m
= a × 10^-10 cm
Volume of unit cell = (a × 10^-10 cm)³
= a³ × 10^-30 cm³

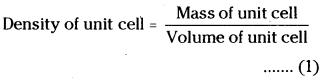
Mass of unit cell = Number of atoms in unit cell × mass of each atom = Z × m
Where Z = number of atoms in unit cell and m = mass of each atom.

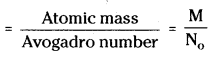
Mass of unit cell = Z × \(\frac{M}{N_o}\)
Substituting in (1) we get
∴ Density of unit cell = \(\frac{\mathrm{Z} \times \mathrm{M}}{\mathrm{a}^3 \times 10^{-30} \times \mathrm{N}_o}\) gm cm^-3

If ‘a’ is in pm, then density will be in g cm^-3. Density of unit cell is the same as the density of the substance. li the density of the metal and dimensions of unit cell are known the atomic mass can be calculated
by using the above equation.

Question 40.
Silver crystallizes In FCC lattice. If edge of the cell is 4.07 × 10^-8cm and density is 10.5 gcm^-3. Calculate the atomic mass of silver.
Answer:
The edge length of unit cell, .
a = 4.077 × 10^-8cm.
Number of atoms in FCC unit cell Z = 4
Density d = 10.5 g cm^-3
Atomic mass M =?
Avogadro constant N₀ = 6.023 × 10²³
We know that density
d = \(\frac{\mathrm{ZM}}{\mathrm{a}^{-3} \mathrm{~N}_{\mathrm{o}}}\) or M = \(\frac{d a^3 \mathrm{~N}_{\mathrm{o}}}{\mathrm{Z}}\)
M = \(\frac{10.5 \times\left(4.077 \times 10^{-8}\right)^3 \times 6.023 \times 10^{23}}{4}\)
= 107.8
∴ Atomic mass of silver = 107.8U

Question 41.
Niobium crystallizes In body – centred cubic structure. If density is 8.55 g cm^-3. Calculate atomic radius of niobium using its atomic mass 93U.
A. Density = 8.55 g cm³
Let length of tie edge = a cm
Volume of unit cell = a³ cm³

Number of atoms per unit cell = 2 (bcc)
Mass of unit cell = \(\frac{2 \times 93}{6.023 \times 10^{23}}\)
Volume of unit cell =

= \(\frac{2 \times 93}{6.023 \times 10^{23} \times 8.55}\) = 36.12 × 10^-24 cm³
∴ a³ = 36.12 × 10^-24 cm³
Edge length a = (36.12 × 10^-4)^1/3
= 3.306 × 10^-8 cm
= 3.306 × 10^-10 m
Now radius, in body centred cubic r = \(\frac{\sqrt{3}}{4} a\)
= \(\frac{\sqrt{3} \times 3.306 \times 10^{-10}}{4}\)
= 1.431 × 10^-10 m
= 0.143 nm. (or) 143 pm.

Question 42.
Copper crystallizes Into a fcc lattice with edge length 3.61 × 10^-8cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm^-3.
Answer:
Volume of the unit cell = (361 × 10^-10)³ cm³
= 47.4 × 10^-24 cm³
Molar mass of copper = 63.5 g mol^-1
In a face centred cubic unit cell, there are four atoms per unit cell.
Mass of unit cell = \(\frac{4 \times 63.5 \mathrm{~g} \mathrm{~mol}^{-1}}{6.02 \times 10^{23} \mathrm{~mol}^{-1}}\)

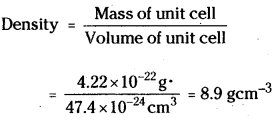
Thus the calculated value of density is in agreement with the measured value of density.

Question 43.
Ferric oxide crystallizes in a hexagonal close packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of ferric oxide.
Answer:
In hexagonal close packed arrangement of oxide ions, each oxide ion has one octahedral hole associated with it.
For each O^2- ion there is one octahedral void in the structure and two of three are occupied by Fe³⁺ ion.
∴ Number of Fe³⁺ ions present per oxide ion = \(\frac{2}{3}\)
Thus the formula of ferric oxide should be Fe_2/3 O₁ or Fe₂ O₃.

Question 44.
Aluminium crystallizes in a cubic close packed structure. Its metallic radius is 125 pm.
(i) What is the length of the side of the unit cell ?
(ii) How many unit cells are there in 1.00 cm3 of aluminium ?
Answer:
i) In cubic close packed structure, the face diagonal of the unit cell is equal to four times the atomic radius.
Face diagonal = 4 × r = 4 × 125 pm = 500 pm
But face diagonal = \(\sqrt{2}\) × edge length

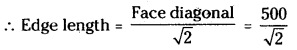
= 354 pm.

ii) Volume of one unit cell = a³
= (3.54 × 10^-8 cm)³
No of unit cells in 1.00 cm³
= \(\frac{100}{\left(3.54 \times 10^{-8}\right)^3}\) = 2.26 × 10²²

Question 45.
How do you obtain the diffraction pattern for a crystalline substance ?
Answer:
The diffraction pattern for a crystalline sub-stance can be obtained by Debye – Scherrer method.

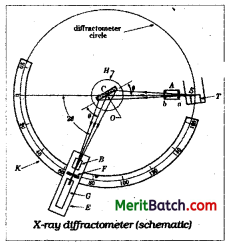
A monochromatic X – ray beam from a source ‘S’ is made incident on a crystal powder sample filled in a thin walled glass capillary tube ‘C’. As a result of diffraction from all sets of lattice planes, diffraction maxima arise which are recorded with a detector placed on the circumference of a circle centred on the powder specimen. The essential features of a diffractometer are shown in figure. A powder specimen C is supported on a table H, which can be rotated about an axis 0 perpendicular to the plane of the drawing. The X – ray source S is also normal to the plane of the drawing and therefore parallel to the diffractometer axis O. X – rays diverge from the source S and are diffracted by the specimen to form con-vergent diffracted beam which comes to a focus at the slit F and then enters ionisation chamber or photographic plate G.

The ioni-sation chamber contains methyl bromide vapours. The energy of the X – rays causes ionisation so that there is a flow of current. The current is measured with electrometer E. The extent of ionisation in the vapours is shown by the electrometer reading. As the intensity of the diffracted X – rays increase, the degree of ionisation also increases. For a set of parallel planes making an angle ‘θ’ with the incident beam of X – rays that satisfy Bragg’s equation, the intensity of the diffracted beam is measured. In Debye – Scherrer powder method the angle 2θ for the diffracted X – rays corresponding to each and every lattice plane is measured along with the intensities of diffracted X – rays with the help of the electrometer. A graph is drawn between the diffracted angle (2θ) and intensity of X – rays. This gives the diffraction pattern for a crystal line substance.

Intext Questions – Answers

Question 1.
Why are solids rigid ?
Answer:
In solids

1. the intermolecular distances are short,
2. intermolecular forces are strong,
3. the constituent particles (atoms, molecules or ions) have fixed positions and can only oscillate about their mean positions. So solids are rigid and incompressible.

Question 2.
Why do solids have a definite volume ?
Answer:
In solids the strong intermolecular forces bring the particles (atoms, molecules or ions) so close that they cling to one another and occupy fixed positions. So solids have definite volume and shape.

Question 3.
Classify the following as amorphous or crystalline solids : Polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper.
Answer:
Amorphous solids : Polyurethane, teflon, cellophane, polyvinyl chloride, fibre glass.
Crystalline solids : Naphthalene, benzoic acid, potassium nitrate, copper.

Question 4.
Why is glass considered a super cooled liquid ?
Answer:
Glass is an amorphous solid. The structure of amorphous solids is similar to that of liquids. So glass is considered as a super cooled liquid.

Question 5.
Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of the solid. Would It show cleavage property?
Answer:
In amorphous solids the particles do not have long range order and their arrangement is irregular along all directions. So the value of any physical property would be same along any direction. This property is known as isotropy.

Question 6.
Classify the following solids into different categories based on the nature of inter- molecular forces operating in them: Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide.
Answer:

1. Molecular solids: Benzene, urea, ammonia, water and argon. Among these benzene and argon contain dispersion or London forces. Urea, ammonia and water contain hydrogen bonding.
2. Ionic solids : Potassium sulphate, zinc sulphide.
3. Metallic solids: Tin, rubidium.
4. Covalent or network solids : Graphite and silicon carbide.

Question 7.
Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it ?
Answer:
In covalent or network solids the adjacent atoms are bonded through covalent bonds throughout the crystal. Covalent bonds are strong and directional in nature, therefore atoms are held very strongly at their positions. Such solids are very hard and brittle. They have extremely high melting points. Hence solid A is covalent solid.

Question 8.
Ionic solids conduct electricity in molten state but not in solid state. Explain.
Answer:
Ionic solids do not conduct electricity in solid state because ions are held by strong electrostatic forces and are not free to move. However, in molten state the ions become free to move. Hence ionic substances conduct electricity in molten state.

Question 9.
What type of solids are electrical conductors, malleable and ductile ?
Answer:
Metallic solids are electrical conductors, malleable and ductile.

Metals are orderly collection of positive ions surrounded by and held together by a sea of free electrons which are mobile and spread throughout the crystal. These free moving electrons are responsible for high electrical and thermal conductivity of metals.

Question 10.
Give the significance of a ‘lattice point’.
Answer:
If the three dimensional arrangement of constituent particles in a crystal is repre-sented diagramatically, in which each particle is depicted as a point, the arrangement is called crystal lattice and the points are called lattice points. Thus a lattice point represents a particle (atom, molecule or ion) in a crystal.

Question 11.
Name the parameters that characterise a unit cell.
Answer:
A unit cell is characterised by

1. its dimensions along the three edges a, b and c. These edges may or may not be mutually perpendicular.
2. Angles between the edges α (between b and c), β (between a and c) and γ (between a and b).
   Thus a unit cell is characterised by six parameters, a, b, c, α, β and γ.

Question 12.
Distinguish between
i) Hexagonal and monoclinic unit cells.
ii) Face centred and end – centred unit cells.
Answer:
(i) In hexagonal unit cell a = b ≠ c and α = β = 90°, γ = 120° but in monoclinic unit cell a ≠ b ≠ c and α = γ = 90°, β ≠ 120°.
(ii) In face centred unit cell a ≠ b ≠ c and α = β = γ = 90° but in end – centred unit cell a ≠ b ≠ c and α = β = γ = 90°.

Question 13.
Explain how much portion of an atom located at
i) corner and
ii) body centre of a cubic unit cell is part of its neighbouring unit cell.
Answer:
i) Each atom at a corner is shared between eight adjacent unit cells. Therefore only \(\frac{1}{8}\)th of an atom belongs to a particular unit cell.
ii) The atom at the body centre wholly belongs to the unit cell in which it is present.

Question 14.
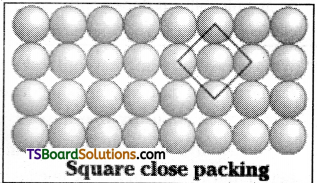
What is the two dimensional coordination number of a molecule in square close – packed layer?
Answer:
In a square close packed layer, the two dimensional coordination number of a molecule is 4.

Question 15.
A compound forms hexagonal close – packed structure. What is the total number of voids in 0.5 mol of it ? How many of these are tetrahedral voids ?
Answer:
Let the number of close packed spheres be ‘N’ then
The number of octahedral voids = N
The number of tetrahedral voids = 2N
∴ Total number of voids = 3N
Since 1 mol of a substance contain N_o (Avogadro number) particles (atoms or molecules or ions). The total number of voids in one mol is 3N_o. In 0.5 mol the total number of voids is 1 .5N_o. Among these the number of tetrahedral voids is 1.0N_o.

Question 16.
A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy 1/3 rd of tetrahedral voids. What is the formula of the compound?
Answer:
In cubic close packing structure with each atom of N there would be two tetrahedral voids. Because only 1/3 rd of tetrahedral voids are occupied by M there would be 2/3 M for each N. Thus formula of the compound is M_2/3 N or M₂N₃.

Question 17.
Which of the following lattices has the highest packing efficiency
i) simple cubic
ii) body centred cubic and
iii) hexagonal close – packed lattice ?
Answer:
The efficiency of
i) simple cubic is 52.4%
ii) body centred cubic is 68% and
iii) hexagonal close – packed lattice is 74%. So hexagonal close – packed lattice has highest packing efficiency.

Question 18.
An element with molar mass 2.7 × 10^-2 kg mol^-1 forms a cubic unit cell with edge length 405 pm. If its density is 2.7 × 10^-3 kg m^-3, what is the nature of the cubic unit cell ?
Answer:
Density d = 2.7 × 10³ kg m^-3
Molar mass M = 2.1 × 10^-2 kg mol^-1
Edge length, a = 405 pm or 405 × 10^-12 m
Density d = \(\frac{\mathrm{Z} \times \mathrm{M}}{\mathrm{a}^3 \times \mathrm{N}_{\mathrm{A}}}\)
or Z = \(\frac{\mathrm{d} \times \mathrm{a}^3 \times \mathrm{N}_{\mathrm{A}}}{\mathrm{M}}\)
= \(\frac{2.7 \times 10^3 \times\left(405 \times 10^{-12}\right)^3 \times 6.022 \times 10^{23}}{2.7 \times 10^{-2}}\) = 4
Since the number of atoms per unit cell is 4 the cubic unit cell must be face centred cube (fcc) (or) ccp. „

Question 19.
What type of defect can arise when a solid is heated ? Which physical property is affected by it and in what way ?
Answer:
On heating a solid vacancy defects may arise. Due to the vacancies the density of the solid would be effected. The density of the solid would decrease due to vacancy defects.

Question 20.
What type of stoichiometric defect is shown by
i) ZnS
ii) AgBr ?
Answer:
i) ZnS shows Frenkel defect.
ii) AgBr shows Frenkel defect as well as Schottky defect.

Question 21.
Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it.
Answer:
If a cation of higher valence is introduced into an ionic solid as impurity, it occupies some site that occupied by host cations. In order to maintain electrical neutrality some host ions are missing from their sites leaving behind vacancies. For example, when Sr²⁺ ions are added to NaCl as impurity, each Sr²⁺ ion replaces two Na⁺ ions. Sr²⁺ ion occupies the site of one Na⁺ ion and the other site remains vacant. Thus, the number of vacancies equal to the number of Sr²⁺ ions added are produced.

Question 22.
Ionic solids, which have anionic vacan-cies due to metal excess defect, develop colour. Explain with the help of a suitable example.
Answer:
The colour is due to the excitation of electrons in F- centres by absorbing energy from visible light falling on the crystals, e.g. the anion vacancies in NaCl impart yellow colour to the compound.

Question 23.
A group 14 element is to be converted into n – type semiconductor by doping it with a suitable impurity. To which group should this impurity belong ?
Answer:
To convert the group 14 element into n -type semiconductor it should be doped with an impurity containing extra electron required for bonding. The impurity element should belong to group -15. It may be phosphorous or arsenic. Silicon doped with group – 15 element behaves as a n – type semiconductor.

Question 24.
What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic ? Justify your answer.
Answer:
Ferromagnetic substances would make better permanent magnets because in ferromagnetic substances all the domains get oriented in one direction. When such a substance is placed in a magnetic field. A strong magnetic effect is produced. These substances remain magnetised even when magnetic field is removed.