TS Inter Second Year Maths 2A Complex Numbers Important Questions Very Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Complex Numbers Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Complex Numbers Important Questions Very Short Answer Type

Question 1.
Find the additive inverse of (√3, 5). [March ’90]
Solution:
Let z = (√3, 5)
The additive inverse of z is – z = – (√3, 5) = (- √3, – 5)

Question 2.
If z = (cos θ, sin θ), find (z – \(\frac{1}{z}\)). [TS – Mar. 2019]
Solution:
Given that z = (cos θ, sin θ)
The multiplicative inverse of z is
z^-1 = \(\frac{1}{z}=\left(\frac{a}{a^2+b^2}, \frac{-b}{a^2+b^2}\right)\)
= \(\left(\frac{\cos \theta}{\cos ^2 \theta+\sin ^2 \theta}, \frac{-\sin \theta}{\cos ^2 \theta+\sin ^2 \theta}\right)\)
= \(\left(\frac{\cos \theta}{1}, \frac{-\sin \theta}{1}\right)\)
= (cos θ – sin θ)
z – \(\frac{1}{z}\) = (cos θ, sin θ) – (cos θ, – sin θ)
= (cos θ – cos θ, sin θ + sin θ)
= (0, 2 sin θ)

Question 3.
Find the multiplicative inverse of (sin θ, cos θ).
Solution:
Let z = (sin θ, cos θ)
The multiplicative inverse of z is
z^-1 = \(\left(\frac{a}{a^2+b^2}, \frac{-b}{a^2+b^2}\right)\)
z^-1 = \(\left(\frac{\sin \theta}{\cos ^2 \theta+\sin ^2 \theta}, \frac{-\cos \theta}{\cos ^2 \theta+\sin ^2 \theta}\right)\)
= \(\left(\frac{\sin \theta}{1}, \frac{-\cos \theta}{1}\right)\)
= (sin θ, – cos θ)

Question 4.
Express \(\frac{4+2 i}{1-2 i}+\frac{3+4 i}{2+3 i}\) in the form a + ib.
Solution:

Question 5.
Find the real and imaginary parts of the complex number \(\frac{a+i b}{a-i b}\). [TS – Mar. 2015]
Solution:

Question 6.
Express (1 – i)³ (1 + i) in the form a + ib.
Solution:
Let z = (1 – i)³ (1 + i)
= (1 – i)² (1 – i) (1 + i)
= (1 + i² – 2i) (1 – i²)
= (1 – 1 – 2i) (1 – (- 1)) (∵ i² = – 1)
= (- 2i) (2)
= – 4i = 0 + i (- 4)
It is in the form a + ib.

Question 7.
Find the multiplicative inverse of 7 + 24i. [TS – Mar. 2016, AP – May 2015]
Solution:
Let z = 7 + 24i
z^-1 = \(\)
∴ The multiplicative inverse of complex number z = 7 + 24i is
z = \(\left(\frac{7-24 i}{7^2+(24)^2}\right)\)
= \(\left(\frac{7-24 \mathrm{i}}{49+576}\right)=\frac{7-24 \mathrm{i}}{625}\) .

Question 8.
If 4x + i(3x – y) = 3 – 6i where x and y are real numbers, then find the values of\ x and y.
Solution:
Given that 4x + i(3x – y) = 3 – 6i
Comparing real and imaginary parts on both sides
4x = 3
x = \(\frac{3}{4}\)

3x – y = – 6
3 (\(\frac{3}{4}\)) – y = – 6
y = \(\frac{9}{4}\) + 6
= \(\frac{9+24}{4}\)
= \(\frac{33}{4}\)
∴ x = \(\frac{3}{4}\), y = \(\frac{33}{4}\)

Question 9.
Find the complex conjugate of (3 + 4i) (2 – 3i). [May ’14, Mar. 1997, AP – Mar. ’18, May ’16]
Solution:
Let z = (3 + 4i) (2 – 3i)
= 6 – 9i + 8i – 12i²
= 6 – i + 12
z = 18 – i
∴ The conjugate of z is \(\overline{\mathrm{z}}=\overline{(18-\mathrm{i})}\) = 18 + ¡

Question 10.
Find the square root of – 5 + 12i. [Board Paper]
Solution:

Question 11.
Find the square root of – 47 + i. 8√3. [March ’13(old), May ’12, ’09, May ’10, ’03]
Solution:

Question 12.
Simplify i² + i⁴ + i⁶ + …………… + (2n + 1) terms.
Solution:
= i² + i⁴ + i⁶ + …………… + (2n + 1) terms
= i² + (i²)² + (i²)³ + …………….. + (2n + 1) terms
= – 1 + 1 – 1 + ……………. + (2n + 1) terms = – 1

Question 13.
Simplify i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (- i)²⁶.
Solution:
i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (- i)²⁶.
= (i²)⁹ – 3 (i²)³ . i + i² (1 + (i²)²) (i²)¹³
= (- 1)⁹ – 3 (- 1)³ . i + (- 1) (1 + (- 1)²) (- 1)¹³
= – 1 + 3i + 2 = 1 + 3i

Question 14.
If (a + ib)² = x + iy, find x² + y². [TS – May 2015]
Solution:
Given that,
(a + ib)² = x + iy
a² + i²b² + 2abi = x + iy
a² – b² + i(2ab) =x + iy
Comparing real and imaginary parts on both sides
x = a² – b², y = 2ab
∴ x² + y² = (a² + b²)² + 4a²b² = (a² + b²)²

Question 15.
Find the least positive integers n, satisfying \(\left(\frac{1+i}{1-i}\right)^n\) = 1.
Solution:

If n = 4
⇒ i⁴ = 1
∴ The required least positive integer, n = 4.

Question 16.
Write z = – √7 + i √21 in the polar form. [AP – May 2015; March 11]
Solution:

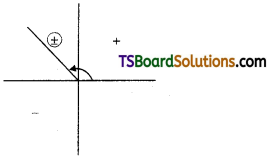
Let, z = – √7 + i √21
= r (cos θ + i sin θ)
then r cos θ = – √7, r sin θ = √21
r = \(\sqrt{x^2+y^2}=\sqrt{(-\sqrt{7})^2+(\sqrt{21})^2}\)
= \(\sqrt{7+21}=\sqrt{28}=2 \sqrt{7}\)
Hence,
2√7 cos θ = – √7
cos θ = \(-\frac{1}{2}\)
2√7 sin θ = √21
2√7 sin θ = √3 . √7
sin θ = \(\frac{\sqrt{3}}{2}\)
∴ θ lies in the Q2.
∴ θ = \(\frac{2 \pi}{3}\)
∴ z = – √7 + i√21
= 2√7 (cos \(\frac{2 \pi}{3}\) + i sin \(\frac{2 \pi}{3}\)).

Question 17.
Express – 1 – i in polar form with principle value of the amplitude.
Solution:

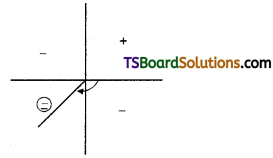
Let, – 1 – i = r (cos θ + i sin θ)
Then r cos θ = – 1; r sin θ = – 1
r = \(\sqrt{(-1)^2+(-1)^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = – 1
cos θ = \(\frac{-1}{\sqrt{2}}\)
∴ θ lies in the Q3.
∴ θ = – \(\frac{3 \pi}{4}\)

√2 sin θ = – 1
sin θ = \(\frac{-1}{\sqrt{2}}\)

∴ – 1 – i = √2 (cos (- \(\frac{3 \pi}{4}\)) + i sin (- \(\frac{3 \pi}{4}\)))

Question 18.
Express – 1 – i√3 in the modulus amplitude form.
Solution:

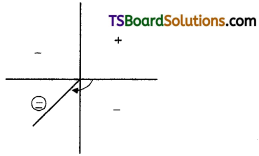
Let – 1 – i√3 = r (cos θ + i sin θ)
Then r cos θ = – 1, r sin θ = – √3
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}\)
= \(\sqrt{(-1)^2+(-\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence, 2 cos θ = – 1, 2 sin θ = – √3
cos θ = – \(\frac{1}{2}\), sin θ = \(\frac{-\sqrt{3}}{2}\)
∴ θ lies in the Q3.
∴ θ = – \(\frac{2 \pi}{3}\)
∴ For the given complex number modulus = 2
Principle amplitude = – \(\frac{2 \pi}{3}\)
∴ – 1 – i √3 = 2 [cos (- \(\frac{2 \pi}{3}\)) + i sin (- \(\frac{2 \pi}{3}\))]

Question 19.
If z₁ = – 1 and z₂ = – 1 then find Arg(z₁z₂).
Solution:
Given, z₁ = – 1
= cos π + i sin π
∴ Arg z₁ = π
z₂ = – i
= cos (- \(\frac{\pi}{2}\)) + i sin (- \(\frac{\pi}{2}\))
∴ Arg z₂ = – \(\frac{\pi}{2}\)
Now,
Arg (z₁z₂) = Arg z₁ + Arg z₂
= π – \(\frac{\pi}{2}\) = \(\frac{\pi}{2}\)

Question 20.
If z₁ = – 1, z₂ = i, then find Arg (\(\frac{z_1}{z_2}\)).
[May 14 11, March 09 Board Paper TS-Mar. 16; AP – Mar. 18, 17]
Solution:
Given z₁ = – 1
= cos π + i sin π
∴ Arg z₁ = π
z₂ = i
= cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
∴ Arg z₂ = \(\frac{\pi}{2}\)
Now, Arg \(\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}\right)\) = Arg z₁ – Arg z₂
= π – \(\frac{\pi}{2}\) = \(\frac{\pi}{2}\)

Question 21.
If (cos 2α + i sin 2α) (cos 2β + i sin 2β) = cos θ + i sin θ, then find the value of θ.
Solution:
Given,
(cos 2α + i sin 2α) (cos 2β + i sin 2β) = cos θ + i sin θ
cis (2α) . cis (2β) = cis θ
cis (2α + 2β) = cis θ
cos (2α + 2β) + i sin (2α + 2β) = cos θ + i sin θ
Comparing real parts on both sides, we get
cos θ = (2α + 2β)
θ = 2 (α + β)

Question 22.
If √3 + i = r (cos θ + i sin θ) then find the value of θ in radian measure.
Solution:

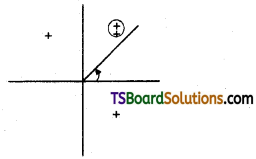
Given that,
√3 + i = r (cos θ + i sin θ)
Then r cos θ = √3, r sin θ = 1
r = \(\sqrt{x^2+y^2}=\sqrt{(\sqrt{3})^2+(1)^2}\)
= \(\sqrt{3+1}=\sqrt{4}\) = 2
Hence,
2 cos θ = √3
cos θ = \(\frac{\sqrt{3}}{2}\)
2 sin θ = 1
sin θ = \(\frac{1}{2}\)
∴ θ lies in the Q1.
∴ θ = \(\frac{\pi}{6}\)

Question 23.
If x + iy = cis α . cis β, then find the value of x² + y². [AP – Mar. 18]
Sol.
Given that,
x + iy = cis α . cis β
= cis (α + β)
= cos (α + β) + i sin (α + β)
Now, comparing real parts on both sides.
we get x = cos (α + β)
Comparing imaginary parts on both sides
we get y = sin (α + β)
Now,
x² + y² = cos² (α + β) + sin² (α + β) = 1.

Question 24.
If (√3 + i)¹⁰⁰ = 2⁹⁹ (a + ib) then show that a² + b² = 4. [AP – Mar.2016] [AP – Mar. 2019]
Solution:
Given that,
(√3 + i)¹⁰⁰ = 2⁹⁹ (a + ib)

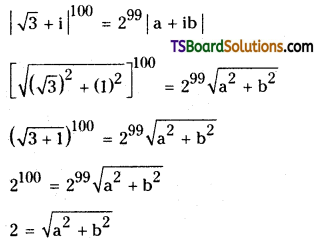
Squaring on both sides,
a² + b² = 4

Question 25.
If z = x + iy and |z| = 1, then find the locus of z. [TS – Mar. 2019]
Solution:
Given, z = x + iy
|z| = 1
|x + iy| = 1
\(\sqrt{x^2+y^2}\) = 1
Squaring on both sides,
x² + y² = 1
∴ Locus of z is x² + y² = 1.

Question 26.
If the amplitude of (z – 1) is \(\frac{\pi}{2}\) then find the locus of z. [TS – May 2015]
Solution:
Let, z = x + iy
Now, z – 1 = x + iy – 1
= (x – 1) + iy
If z = x + iy then θ = tan^-1 (\(\frac{y}{x}\))
Given that,
the amplitude of (z – 1) is \(\frac{\pi}{2}\)
tan^-1 (\(\frac{y}{x-1}\)) = \(\frac{\pi}{2}\)
\(\frac{y}{x-1}\) = tan \(\frac{\pi}{2}\)
\(\frac{y}{x-1}\) = ∞ = \(\frac{1}{0}\)
x – 1 = 0
x = 1
∴ Locus of z is x = 1.

Question 27.
If the Arg \(\overline{\mathbf{z}}_1\) and Arg z₂ are \(\frac{\pi}{5}\) and \(\frac{\pi}{3}\) respectively, then find (Arg z₁ + Arg z₂). [AP-May, Mar. 2016]
Solution:
If z = x + iy then θ = tan^-1 (\(\frac{y}{x}\))
If \(\overline{\mathrm{Z}}\) = x – iy then θ = tan^-1 (\(\frac{-y}{x}\))
= – tan^-1 (\(\frac{y}{x}\))
Given that,
Arg \(\overline{\mathbf{z}}_1\) = \(\frac{\pi}{5}\)
Arg z₁ = – \(\frac{\pi}{5}\)
Arg z₂ = \(\frac{\pi}{3}\)
Now,
Arg z₁ + Arg z₂ = – \(\frac{\pi}{5}\) + \(\frac{\pi}{3}\)
= \(\frac{-3 \pi+5 \pi}{15}=\frac{2 \pi}{15}\).

Question 28.
If z = \(\frac{1+2 i}{1-(1-i)^2}\) then find Arg(z).
Solution:
z = \(\frac{1+2 i}{1-(1-i)^2}\)
= \(\frac{1+2 \mathrm{i}}{1-\left(1+\mathrm{i}^2-2 \mathrm{i}\right)}\)
= \(\frac{1+2 i}{1-1-i^2+2 i}\)
= \(\frac{1+2 \mathrm{i}}{1+2 \mathrm{i}}\) = 1
∴ z = 1 = 1 + i(0)
∴ Arg z = tan^-1 (\(\frac{y}{x}\))
= tan^-1 (\(\frac{0}{1}\))
= tan (0) = 0°

Question 29.
Simplify \(\frac{(2+4 i)(-1+2 i)}{(-1-i)(3-i)}\) and find its modulus.
Solution:
Given,

Question 30.
Simplify \(\frac{(1+i)^3}{(2+i)(1+2 i)}\) and find its modulus.
Solution:
Given, \(\frac{(1+i)^3}{(2+i)(1+2 i)}\)

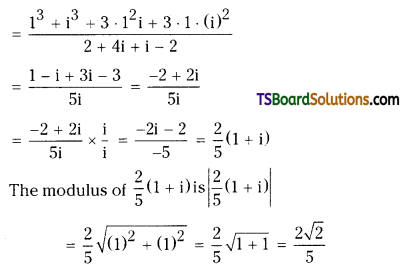
Question 31.
If (1 – i) (2 – i) (3 – i) ……….. (1 – ni) = x – iy, then prove that 2 . 5 . 10 …………….. (1 + n²) = x² + y².
Solution:
Given that,
(1 – i) (2 – i) (3 – i) (1 – ni) = x – iy

Squaring on bothsides,
2 . 5 . 10 . …………… (1 + n²) = x² + y².

Question 32.
If the real part of \(\frac{z+1}{z+i}\) is 1, then find the locus of z.
Solution:
Let, z = x + iy
Now,

Given that,
the real part of \(\frac{z+1}{z+i}\) is 1.
⇒ \(\frac{x^2+x+y^2+y}{x^2+(y+1)^2}\) = 0
x² + y² + x + y = x² + y² + 2y + 1
x – y – 1 = 0
∴ The locus of z is x – y – 1 = 0.

Question 33.
If |z – 3 + i| = 4 determine the locus of z. [March 14, May 08]
Solution:
Let z = x + iy
Given, |z – 3 + i| = 4
|x + iy – 3 + i| = 4
|(x – 3) + i (y + 1)| = 4
\(\sqrt{(\mathrm{x}-3)^2+(\mathrm{y}+1)^2}\) = 4
Squaring on both sides
(x – 3)² + (y + 1)² = 16
x² + 9 – 6x + y² + 2y + 1 – 16 = 0
x² + y² – 6x + 2y – 6 = 0
∴ The locus of z is x² + y² – 6x – 2y – 6 = 0.

Question 34.
If |z + ai| = |z – ai|, then find the locus of z.
Solution:
Let, z = x + iy
Given, |z + ai| = |z – ai|
|x + iy + ai| = |x – iy – ai|
|x + i(y + a)| = |x + i(y – a)|
\(\sqrt{(x)^2+(y+a)^2}=\sqrt{(x)^2+(y-a)^2}\)
Squaring on both sides
x² + (y + a)² = x² + (y – a)²
(y + a)² – (y – a)² = 0
4ya = 0
y = 0
∴ The locus of z is y = 0.

Question 35.
Find the equation of the straight line joining the points represented by (- 4 + 3i), (2 – 3i) in the Argand plane.
Solution:
Let the two complex numbers be represented in the Argand plane by the points P, Q respectively.
Then P = (- 4, 3), Q = (2, – 3)
∴ The equation of \(\overline{\mathrm{PQ}}\) is
y – y₁ = \(\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathrm{x}_2-\mathrm{x}_1}\) (x – x₁)
y – 3 = \(\frac{-3-3}{2+4}\) (x + 4)
y – 3 = \(\frac{-6}{6}\) (x + 4)
y – 3 = – 1 (x + 4)
y – 3 = – x – 4
x + y + 1 = 0.

Question 36.
z = x + iy represents a point in the Argand plane. Find the locus of z such that z = 2.
Solution:
Given, z = x + iy
=> P = (x, y)
|z| = 2
|x + iy| = 2
\(\sqrt{\mathrm{x}^2+\mathrm{y}^2}\) = 2
Squaring on both sides
x² + y² = 4
x² + y² – 4 = 0
∴ Locus of P is x² + y² – 4 = 0
The locus represents a circle with centre (0, 0) and radius 2 units.

Question 37.
The point ‘P’ represents a complex number z in the Argand plane. If the amplitude of z is \(\frac{\pi}{4}\), determine the locus of P.
Solution:
Let z = x + iy
⇒ P = (x, y)
Given that,
Amp(z) = \(\frac{\pi}{4}\)
tan^-1 (\(\frac{y}{x}\)) = \(\frac{\pi}{4}\)
\(\frac{y}{x}\) = tan \(\frac{\pi}{4}\)
\(\frac{y}{x}\) = 1
y = x
x = y
∴ Locus of P is x = y i.e., x – y = 0.
The locus represents a line passing through origin and making an angle of 45° with the (+) ve direction of X – axis.

Question 38.
Find the equation of the perpendicular bisector of the line segment joining the points 7 + 7i, 7 – 7i in the Argand plane.
Solution:

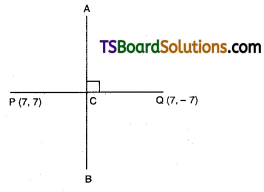
Let the two complex numbers be represented in the Argand plane by the points P, Q respectively.
Then P = (7, 7), Q = (7, – 7)
Since, C is the midpoint of \(\overline{\mathrm{PQ}}\) then
C = \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2}{2}, \frac{\mathrm{y}_1+\mathrm{y}_2}{2}\right)\)
= \(\left(\frac{7+7}{2}, \frac{7-7}{2}\right)=\left(\frac{14}{2}, \frac{0}{2}\right)\) = (7, 0)
Slope of \(\overline{\mathrm{PQ}}\) is m = \(\frac{y_2-y_1}{x_2-x_1}\)
= \(\frac{-7-7}{7-7}=\frac{-14}{0}\)
∵ \(\overline{\mathrm{AB}}\) is ⊥ to \(\overline{\mathrm{PQ}}\) then
slope of \(\overline{\mathrm{AB}}\) = \(\frac{-1}{\mathrm{~m}}=\frac{-1}{\frac{-14}{0}}\) = o
The equation of the straight line \(\overline{\mathrm{AB}}\) is
y – y₁ = \(-\frac{1}{m}\) (x – x₁)
y – 0 = 0 (x – 7)
⇒ y = 0.

Question 39.
Find the equation of the straight line joining the points – 9 + 6i, 11 – 4i in the Argand plane.
Solution:
Let the two complex numbers be represented in the Argand plane by the point P, Q respectively.
Then P = (- 9, 6), Q = (11, – 4)
∴ The equation of \(\overline{\mathrm{PQ}}\) is
y – y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x – x₁)
y – 6 = \(\frac{-4-6}{11+9}\) (x + 9)
y-6 = \(\frac{-10}{20}\) (x + 9)
y – 6 = \(\frac{-1}{2}\) (x + 9)
2y – 12 = – x – 9
x + 2y – 3 = 0.

Question 40.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i – 2 – 2i, – 2√3 + 2√3i are the vertices of an equilateral triangle. [AP – May 15, 07, TS-Mar. 18]
Solution:
Let the three complex numbers be represented in the Argand plane by the points P, Q, R respectively.
Then P = (2, 2), Q = (- 2, – 2). R = (- 2√3, 2√3)
Now,
PQ = \(\sqrt{(2+2)^2+(2+2)^2}\)
= \(\sqrt{(4)^2+(4)^2}=\sqrt{16+16}=\sqrt{32}\)

QR = \(\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2}\)
= \(\sqrt{4+12-8 \sqrt{3}+4+12+8 \sqrt{3}}=\sqrt{32}\)

PR = \(\sqrt{(2+2 \sqrt{3})^2+(2-2 \sqrt{3})^2}\)
= \(\sqrt{4+12+8 \sqrt{3}+4+12-8 \sqrt{3}}=\sqrt{32}\)

∴ PQ = QR = PR
∴ Given points form an equilateral triangle.

Question 41.
If z = 2 – 3i, then show that z² – 4z + 13 = 0. [TS- Mar. 18, Mar. 08, AP – Mar. 2019]
Solution:
Given that z = 2 – 3i
z – 2 = – 3i
Squaring on both sides
(z – 2)² = (- 3i)²
z² + 4 – 4z = 9i²
z² – 4z + 4 = – 9
∴ z² – 4z + 13 = 0

Question 42.
Find the multiplicative inverse of (3, 4).
Solution:
(\(\frac{3}{25}\), \(\frac{4}{25}\))

Question 43.
Write \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\) in the form of a + ib.
Solution:
\(\frac{-8}{13}\) + i (0)

Question 44.
Write the complex number (1 + 2i)³ in the form a + ib. [TS – Mar. 2017]
Solution:
– 11 – 2i

Question 45.
Find the multiplicative inverse of √5 + 3i.
Solution:
\(\frac{\sqrt{5}}{14}-\frac{3}{14} i\)

Question 46.
Write the conjugate of (2 + 5i) (- 4 + 6i).
Solution:
– 38 + 8i.

Question 47.
Find the square roots of 3 + 4i. [March ’13 (old). May ’12, ’09, May ’10, ’03]
Solution:
± (2 + i)

Question 48.
Find the square roots of 7 + 24i. [TS – May 2016, Mar. ‘14]
Solution:
± (4 + 3i)

Question 49.
Find the square roots of – 8 – 6i.
Solution:
± (1 – 3i)