TS Inter Second Year Maths 2B Circles Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Circles Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Circles Important Questions Very Short Answer Type

Question 1.
Find the centre and radius of the circle x² + y² + 6x + 8y – 96 = 0. (Mar. ’94)
Solution:
Given the equation of the circle is
x² + y² + 6x + 8y – 96 = 0 …….(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
We get 2g = 6 ⇒ g = 3
2f = 8 ⇒ f = 4
c = -96
Centre c = (-g, -f) = (-3, -4)
radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(3)^2+(4)^2+96}\)
= √121
= 11

Question 2.
Find the centre and radius of the circle x² + y² + 2x – 4y – 4 = 0
Solution:
Given the equation of the circle is
x² + y² + 2x – 4y – 4 = 0 …….(1)
Comparing (1) with
x² + y² + 2gx + 2fy + c = 0
We get 2g = 2 ⇒ g = 1
2f = -4 ⇒ f = -2
c = -4
Centre c = (-g, -f) = (-1, 2)
radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(1)^2+(-2)^2+4}\)
= √9
= 3

Question 3.
Find the centre and radius of the circle x² + y² + 2ax – 2by + b² = 0
Solution:
Given the equation of the circle is
x² + y² + 2ax – 2by + b2 = 0 …….(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
We get 2g = 2a ⇒ g = a
2f = -2b ⇒ f = -b
c = b²
Centre c = (-g, -f) = (-a, b)
radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(a)^2+(-b)^2-b^2}\)
= √a²
= a

Question 4.
Find the centre and radius of the circle 3x² + 3y² – 6x + 4y – 4 = 0.
Solution:
Given equation of the circle is 3x² + 3y² – 6x + 4y – 4 = 0
⇒ x² + y² – 2x + \(\frac{4}{3}\)y – \(\frac{4}{3}\) = 0 ………(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0

Question 5.
Find the centre and radius of the circle \(\sqrt{1+\mathrm{m}^2}\) (x² + y²) – 2cx – 2mcy = 0. (May ’10)
Solution:

Question 6.
If the circle x² + y² + ax + by – 12 = 0 has the centre at (2, 3), then find a, b, and the radius of the circle. (May ’09, ’07, Mar. ’08)
Solution:
Given the equation of the circle is
x² + y² + ax + by – 12 = 0 ……..(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
we get 2g = a ⇒ g = \(\frac{a}{2}\)
2f = b ⇒ f = \(\frac{b}{2}\)
c = -12

Question 7.
If x² + y² + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3). Find g, f, and its radius. [(AP) May ’19]
Solution:
Given the equation of the circle is
x² + y² + 2gx + 2fy – 12 = 0 ……..(1)
Centre of (1) is C = (-g, -f)
Given that centre C = (2, 3)
∴ (-g, -f) = (2, 3)
⇒ g = -2, f = -3
Now Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(-2)^2+(-3)^2-(-12)}\)
= √25
= 5

Question 8.
If x² + y² + 2gx + 2fy = 0 represents a circle with centre (-4, -3) then find g, f, and the radius of the circle. [(AP) May ’17]
Solution:
Given the equation of the circle is
x² + y² + 2gx + 2fy = 0 …….(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
we get g = g, f = f, c = 0
Centre of (1) is C = (-g, -f)
Given that centre, C = (-4, -3)
∴ (-g, -f) = (-4, -3)
we get g = 4, f = 3
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(4)^2+(3)^2-0}\)
= √25
= 5

Question 9.
Find the value of ‘a’, if 2x² + ay² – 3x + 2y – 1 = 0 represents a circle, and also find its radius. [(AP) Mar. ’15]
Solution:
Given equation is
2x² + ay² – 3x + 2y – 1 = 0 …….(1)
Comparing (1) with
ax² + 2hxy + by² + 2gx + 2fy + c = 0
We get a = 2, h = 0, b = a, g = \(\frac{-3}{2}\), f = 1, c = -1
Now, equation (1) represents a circle
then a = b
⇒ 2 = a
∴ a = 2
The equation of the circle is
2x² + 2y² – 3x + 2y – 1 = 0
\(x^2+y^2-\frac{3}{2} x+y-\frac{1}{2}=0\)
Comparing the above equation with x² + y² + 2gx + 2fy + c = 0

Question 10.
If the circle x² + y² – 4x + 6y + a = 0 has a radius of 4 then find ‘a’. [(AP) Mar. ’16]
Solution:
Given the equation of the circle is
x² + y² – 4x + 6y + a = 0 …….(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
We get 2g = -4 ⇒ g = -2
2f = 6 ⇒ f = 3
c = a
Given that Radius, r = 4
⇒ \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=4\)
⇒ \(\sqrt{(-2)^2+(3)^2-a}=4\)
⇒ \(\sqrt{4+9-a}\) = 4
⇒ \(\sqrt{13-\mathrm{a}}\) = 4
Squaring on both sides
13 – a = 16
⇒ 13 – 16 = a
⇒ a = -3
∴ a = -3

Question 11.
If x² + y² – 4x + 6y + c = 0 represents a circle with a radius of 6 then find the value of ‘c’.
Solution:
Given equation of the circle is x² + y² – 4x + 6y + c = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -2, f = 3, c = c
Given that radius r = 6
⇒ \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}=6\)
⇒ \(\sqrt{(-2)^2+(3)^2-c}=6\)
⇒ \(\sqrt{4+9-\mathrm{c}}\)
⇒ \(\sqrt{13-c}=6\)
Squaring on both sides
13 – c = 36
⇒ 13 – 36 = c
⇒ c = -23

Question 12.
Find the equation of the circle passing through (-2, 3) having the centre at (0, 0).
Solution:

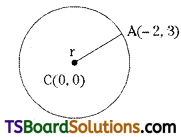
Given centre C(h, k) = (0, 0)
Let the given point A (-2, 3)
Since A(-2, 3) is a point on the circle.
Radius r = CA = \(\sqrt{(-2-0)^2+(3-0)^2}\) = √13
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 0)² + (y – 0)² = (√13)²
⇒ x² + y² = 13
⇒ x² + y² – 13 = 0

Question 13.
Find the equation of the circle passing through the origin and having the centre at (-4, -3). (Mar. ’04; May ’02)
Solution:
Given centre, C(h, k) = (-4, -3)
Let, the given point A(0, 0).
Since, A(0, 0) is a point on the circle.
∴ Radius, r = CA = \(\sqrt{(-4-0)^2+(-3-0)^2}\)
= √25
= 5
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x + 4)²+ (y + 3)² = (5)²
⇒ x² + 16 + 8x + y² + 9 + 6y = 25
⇒ x² + y² + 8x + 6y + 25 = 25
⇒ x² + y² + 8x + 6y = 0

Question 14.
Find the equation of the circle passing through (3, 4) and having the centre at (-3, 4).
Solution:
Given centre C(h, k) = (-3, 4)
Let the given point A = (3, 4)

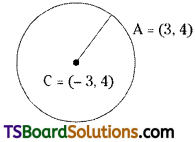
Since ‘A’ is the point on the circle.
∴ Radius, r = CA = \(\sqrt{(-3-3)^2+(4-4)^2}\)
= √36
= 6
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x + 3)² + (y – 4)² = 6²
⇒ x² + 9 + 6x + y² + 16 – 8y = 36
⇒ x² + y² + 6x – 8y – 11 = 0

Question 15.
Find the equation of the circle which is concentric with x² + y² – 6x – 4y – 12 = 0 and passing through (-2, 14). [(TS) May ’17; Mar & May ’14]
Solution:

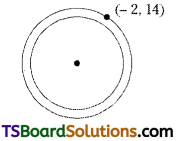
Given equation of the circle is x² + y² – 6x – 4y – 12 = 0
Equation of the circle concentric with the circle
x² + y² – 6x – 4y – 12 = 0 is x² + y² – 6x – 4y + k = 0 …….(1)
Equation (1) passes through (-2, 14) then
(-2)² + (14)² – 6(-2) – 4(14) + k = 0
⇒ 4 + 196 + 12 – 56 + k = 0
⇒ 156 + k = 0
⇒ k = -156
The required circle from (1) is x² + y² – 6x – 4y – 156 = 0.

Question 16.
Find the equation of the circle with (-4, 3), (3, -4) as ends of a diameter.
Solution:
Let A = (x₁, y₁) = (-4, 3), B = (x₂, y₂) = (3, -4) are the given points.
∴ The required equation of the circle is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x + 4) (x – 3) + (y – 3) (y + 4) = 0
⇒ x² – 3x + 4x – 12 + y² + 4y – 3y – 12 = 0
⇒ x² + y² + x + y – 24 = 0

Question 17.
Find the other end of the diameter of the circle x² + y² – 8x – 8y + 27 = 0 if one end of it is (2, 3). [(AP) Mar. ’20; May ’12]
Solution:
Given the equation of the circle is x² + y² – 8x – 8y + 27 = 0.
Let A(2, 3) be the given point.
Comparing (1) with x² + y² + 2gx + 2fy + c = 0, we get
g = -4, f = -4, c = 27
Centre of the circle, C(h, k) = (-g, -f) = (4, 4)
Let, B(x, y) be the other end of the diameter

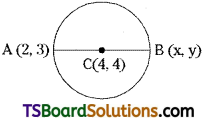
∵ ‘C’ is the midpoint of \(\overline{\mathrm{AB}}\) then (4, 4) = \(\left(\frac{2+x}{2}, \frac{3+y}{2}\right)\)
\(\frac{2+x}{2}\) = 4
⇒ 2 + x = 8
⇒ x = 8 – 2
⇒ x = 6
\(\frac{3+y}{2}\) = 4
⇒ 3 + y = 8
⇒ y = 8 – 3
⇒ y = 5
∴ The other end of the diameter is B = (6, 5).

Question 18.
Obtain the parametric equation of the circle represented by x² + y² = 4. (Mar. ’14)
Solution:
Given the equation of the circle is x² + y² = 4
This is of the form x² + y² = r²
Centre C = (h, k) = (0, 0); Radius r = 2
∴ The parametric equations of the circle are
x = h + r cos θ = 0 + 2 cos θ = 2 cos θ
y = k + r sin θ = 0 + 2 sin θ = 2 sin θ
0 ≤ θ ≤ 2π

Question 19.
Find the parametric equations of the circle (x – 3)² + (y – 4)² = 8². [Mar. ’18, ’16 (AP)]
Solution:
Given equation of the circle is (x – 3)² + (y – 4)² = 8²
This is of the form (x – h)² + (y – k)² = r²
we get h = 3, k = 4, r = 8
∴ Centre (h, k) = (3, 4)
Radius r = 8
∴ The parametric equations are
x = h + r cos θ = 3 + 8 cos θ
y = k + r sin θ = 4 + 8 sin θ
0 ≤ θ ≤ 2π

Question 20.
Obtain the parametric equations of the circle represented by x² + y² + 6x + 8y – 96 = 0.
Solution:
Given the equation of the circle is
x² + y² + 6x + 8y – 96 = 0 …….(1)
Comparing (1) with
x² + y² + 2gx + 2fy + c = 0, we get
2g = 6 ⇒ g = 3
2f = 8 ⇒ f = 4
c = -96
Centre, C(h, k) = (-g, -f) = (-3, -4)
Radius, r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{3^2+4^2+96}\)
= √121
= 11
The parametric equations of the circle are
x = h + r cos θ = -3 + 11 cos θ
y = k + r sin θ = -4 + 11 sin θ
0 ≤ θ ≤ 2π

Question 21.
Find the parametric equations of the circle x² + y² – 6x + 4y – 12 = 0. [(AP) May ’15; Mar. ’10, ’06]
Solution:
Given the equation of the circle is
x² + y² – 6x + 4y – 12 = 0 ……….(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0, we get
2g = -6 ⇒ g = -3
2f = 4 ⇒ f = 2
f = -12
Centre, C(h, k) = (-g, -f) = (3, -2)
Radius, r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(-3)^2+(2)^2+12}\)
= √25
= 5
The parametric equations of the circle are
x = h + r cos θ = 3 + 5 cos θ
y = k + r sin θ = -2 + 5 sin θ
0 ≤ θ ≤ 2π

Question 22.
Find the length of the tangent from (3, 3) to the circle x² + y² + 6x + 18y + 26 = 0. (Mar. ’05)
Solution:
Given equation of the circle is x² + y² + 6x + 18y + 26 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we get
g = 3, f = 9, c = 26
Given point P(x₁, y₁) = (3, 3)
Length of the tangent = \(\sqrt{S_{11}}\)
= \(\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}}\)
= \(\sqrt{(3)^2+(3)^2+2(3)(3)+2(9)(3)+26}\)
= \(\sqrt{9+9+18+54+26}\)
= √116

Question 23.
If the length of the tangent from (2, 5) to the circle x² + y² – 5x + 4y + k = 0 is √37, then find k. [(TS) May, Mar. ’18; (AP) May ’17]
Solution:
Given equation of the circle is x² + y² – 5x + 4y + k = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we get
g = \(\frac{-5}{2}\), f = 2, c = k
Let the given point P(x₁, y₁) = (2, 5)
Given that the length of the tangent = √37
∴ \(\sqrt{S_{11}}\) = √37

Question 24.
If the length of the tangent from (5, 4) to the circle x² + y² + 2ky = 0 is 1, then find ‘k’. [(TS) Mar. ’20, ’15, May 15; (AP) May ’18, Mar. ’15; May ‘16, ‘15]
Solution:
The given equation of the circle is x² + y² + 2ky = 0.
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0 we get
g = 0, f = k, c = 0
Let, the given point P(x₁, y₁) = (5, 4)
Given the length of the tangent = 1
\(\sqrt{S_{11}}\) = 1
⇒ S₁₁ = 1
⇒ \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}=1\)
⇒ (5)² + (4)² + 2(0)(5) + 2k(4) + 0 = 1
⇒ 25 + 16 + 8k = 1
⇒ 8k = -40
⇒ k = \(\frac{-40}{8}\) = -5

Question 25.
Show that the line lx + my + n = 0 is normal to the circle S = 0 if and only if lg + mf = n.
Solution:
The straight line lx + my + n = 0 is normal to the circle.
S = x² + y² + 2gx + 2fy + c = 0
If the centre, C(-g, -f) lies on lx + my +n = 0 then
l(-g) + m(-f) + n = 0
⇒ -lg – mf + n = 0
⇒ lg + mf = n

Question 26.
Find the equation of the polar of (2, 3) with respect to the circle x² + y² + 6x + 8y – 96 = 0. [May ’96]
Solution:
Given equation of the circle is x² + y² + 6x + 8y – 96 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
we get g = 3, f = 4, c = -96
Let the given point P(x₁, y₁) = (2, 3)
The equation of polar P(2, 3) w.r.t the given circle is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(2) + y(3) + 3(x + 2) + 4(y + 3) – 96 = 0
⇒ 2x + 3y + 3x + 6 + 4y + 12 – 96 = 0
⇒ 5x + 7y – 78 = 0

Question 27.
Find the polar of (1, -2) with respect to x² + y² – 10x – 10y + 25 = 0. [(TS) Mar. ’15]
Solution:
Given equation of the circle is x² + y² – 10x – 10y + 25 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
We get g = -5, f = -5, c = 25
Let the given point P(x₁, y₁) = (1, -2)
The equation of polar P(1, -2) w.r.t the given circle is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(-2) – 5(x + 1) – 5(y – 2) + 25 = 0
⇒ x – 2y – 5x – 5 – 5y + 10 + 25 = 0
⇒ -4x – 7y + 30 = 0
⇒ 4x + 7y – 30 = 0

Question 28.
Find the value of k if the points (1, 3) and (2, k) are conjugate with respect to the circle x² + y² = 35. [(AP) May ’19, Mar. ’17; (TS) Mar. ’19, ’16, May ’17]
Solution:
Given the equation of the circle is x² + y² = 35
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = 0, f = 0, c = -35
Let, the given points are A(x₁, y₁) = (1, 3), B(x₂, y₂) = (2, k)
Since the given points are conjugate then S₁₂ = 0
⇒ x₁x₂+ y₁y₂+ g(x₁ + x₂) + f(y₁ + y₂) + c = 0
⇒ 1(2) + 300 + 0(1 + 2) + 0(3 + k) – 35 = 0
⇒ 2 + 3k – 35 = 0
⇒ 3k = 33
⇒ k = 11

Question 29.
If(4, k) and (2, 3) are conjugate points with respect to the circle x² + y² = 17 then find k.
Solution:
Given equation of the circle is x² + y² – 17 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
g = 0, f = 0, c = -17
Let, the given points be
A(x₁, y₁) = (4, k), B(x₂, y₂) = (2, 3)
Since the given points are conjugate then
S₁₂ = 0
⇒ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = o
⇒ 4(2) + k(3) + 0(4 + 2) + 0(k + 3) – 17 = 0
⇒ 8 + 3k + 0 + 0 – 17 = 0
⇒ 3k – 9 = 0
⇒ 3k = 9
⇒ k = 3

Question 30.
Find the value of ‘k’ if the points (4, 2) and (k, -3) are conjugate points with respect to the circle x² + y² – 5x + 8y + 6 = 0. [(AP) Mar. ’19; (TS) ’17; May ’14]
Solution:
Given equation of the circle is x² + y2 – 5x + 8y + 6 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0, we get
g = \(\frac{-5}{2}\), f = 4, c = 6
Let the given points are
A(x₁, y₁) = (4, 2) and B(x₂, y₂) = (k, -3)
Since the given points are conjugate then S₁₂ = 0
⇒ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
⇒ 4(k) + 2(-3) + \(\frac{-5}{2}\) (4 + k) + 4(2 – 3) + 6 = 0
⇒ 4k – 6 – 10 – \(\frac{5k}{2}\) – 4 + 6 = 0
⇒ \(\frac{-5k}{2}\) + 4k – 14 = 0
⇒ \(\frac{-5 k+8 k-28}{2}\) = 0
⇒ 3k – 28 = 0
⇒ 3k = 28
⇒ k = \(\frac{28}{3}\)

Question 31.
Find the die equation of the circle with centre (2, -3) and radius 4.
Solution:
Given centre c(h, k) = (2, -3)
radius r = 4
The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y + 3)² = (4)²
⇒ x² + 4 – 4x + y² + 9 + 6y = 16
⇒ x² + y² – 4x + 6y – 3 = 0

Question 32.
Find the equation of the circle with centre (-a, -b) and radius \(\sqrt{\mathbf{a}^2-\mathbf{b}^2}\).
Solution:
Given centre c(h, k) = (-a, -b)
radius r = \(\sqrt{\mathbf{a}^2-\mathbf{b}^2}\)
The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x + a)² + (y + b)² = \(\left(\sqrt{a^2-b^2}\right)^2\)
⇒ x² + a² + 2ax + y² + b² + 2by = a² – b²
⇒ x² + y² + 2ax + 2by + 2b² = 0

Question 33.
Find the equation of the circle with centre c(a, -b) and radius a + b.
Solution:
Given centre c(h, k) = (a, -b)
radius r = a + b
The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x – a)² + (y + b)² = (a + b)²
⇒ x² + a² – 2ax + y² + b² + 2by = a² + b² + 2ab
⇒ x² + y² – 2ax + 2by – 2ab = 0

Question 34.
Find the centre and radius of the circle 3x² + 3y² – 5x – 6y + 4 = 0.
Solution:
Given equation of the circle is 3x² + 3y² – 5x – 6y + 4 = 0

Question 35.
Find the equation of the circle whose extremities of a diameter are (1, 2) and (4, 5).
Solution:
Let A(x₁, y₁) = (1, 2) and B(x₂, y₂) = (4, 5) be the two given points.
∴ The equation of the required circle is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 1)(x – 4) + (y – 2)(y – 5) = 0
⇒ x² – 4x – x + 4 + y² – 2y – 5y + 10 = 0
⇒ x² + y² – 5x – 7y + 14 = 0

Question 36.
Find the position of the point P(3, 4) w.r.t the circle x² + y² – 4x – 6y – 12 = 0.
Solution:
Given equation of the circle is x² + y² – 4x – 6y – 12 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -3, c = -12
Given point P(x₁, y₁) = (3, 4)
Now, S11 = \(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}\)
= (3)² + (4)² + 2(-2)(3) + 2(-3)(4) – 12
= 9 + 16 – 12 – 24 – 12
= 25 – 48
= -23
Since S₁₁ < 0, then the point, P(3, 4) is inside the given circle.

Question 37.
Find the position of the point (1, 5) with respect to the circle x² + y² – 2x – 4y + 3 = 0.
Solution:
Given equation of the circle is x² + y² – 2x – 4y + 3 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
We get g = -1, f = -2, c = 3
Given point P(x₁, y₁) = (1, 5)
Now S11 = \(\mathrm{x}_1{ }^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}\)
= (1)² + (5)² + 2(-1)(1) + 2(-2)(5) + 3
= 1 + 25 – 2 – 20 + 3
= 29 – 22
= 7
Since S₁₁ > 0, then the point, P(1, 5) is outside the given circle.

Question 38.
Find the power of (1, 2) with respect to the circle x² + y² + 6x + 8y – 96 = 0.
Solution:
The given equation of the circle is x² + y² + 6x + 8y – 96 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = 3, f = 4, c = -96
Point P(x₁, y₁) = (1, 2)
∴ The power of P(1, 2) w.r.t the given circle is S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}\)
= (1)² + (2)² + 2(3)(1) + 2(4)(2) – 96
= 1 + 4 + 6 + 16 – 96
= -69

Question 39.
Find the power of the die point (-1, 1) with respect to the circle x² + y² – 6x + 4y – 12 = 0. [(TS) Mar. ’16]
Solution:
The given equation of the circle is x² + y² – 6x + 4y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = -3, f = 2, c = -12
Point P(x₁, y₁) = (-1, 1)
∴ The power of P(-1, 1) w.r.t the given circle is
S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}\)
= (-1)² + (1)² + 2(-3)(-1) + 2(2)(1) – 12
= 1 + 1 + 6 + 4 – 12
= 12 – 12
= 0

Question 40.
Find the length of the tangent from (2, 5) to the circle x² + y² – 5x + 4y – 5 = 0.
Solution:
The given equation of the circle is x² + y² – 5x + 4y – 5 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0,
we get g = \(\frac{-5}{2}\), f = 2, c = -5
Point, P(x₁, y₁) = (2, 5)
∴ The length of the tangent = \(\sqrt{S_{11}}\)

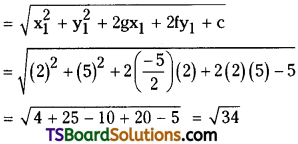
Question 41.
Find the length of the tangent from (-2, 5) to the circle x² + y² – 25 = 0. [(TS) May ’16]
Solution:
The given equation of the circle is x² + y² – 25 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = 0, f = 0, c = -25
Point P(x₁, y₁) = (-2, 5)
∴ The length of the tangent = \(\sqrt{S_{11}}\)

Question 42.
Find the length of the tangent from (12, 17) to the circle x² + y² – 6x – 8y – 25 = 0.
Solution:
The given equation of the circle is x² + y² – 6x – 8y – 25 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0,
We get g = -3, f = -4, c = -25
Point P(x₁, y₁) = (12, 17)
∴ The length of the tangent = \(\sqrt{S_{11}}\)

Question 43.
Find the equation of the tangent at P(-1, 1) of the circle x² + y² – 6x + 4y – 12 = 0. [(TS) Mar. ’16]
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = -3, f = 2, c = -12
The given point P(x₁, y₁) = (-1, 1)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-1) + y(1) + (-3) (x – 1) + 2(y + 1) + c = 0
⇒ -x + y – 3x + 3 + 2y + 2 – 12 = 0
⇒ -4x + 3y – 7 = 0
⇒ 4x – 3y + 7 = 0

Question 44.
Find the area of the triangle formed by the tangent at P(x1, y1) to the circle x² + y² = a² with the coordinate axes. [(AP) Mar. ’20; Apr. ’00, ’98, ’93]
Solution:
Given the equation of the circle is x² + y² = a²
The equation of the tangent at P(x₁, y₁) to the given circle is S₁ = 0.

Question 45.
Find the chord of contact of (1, 1) w.r.t the circle x² + y² = 9. [(AP) Mar. ’20]
Solution:
Given the equation of the circle is x² + y² = 9
Comparing this equation with x² + y² + 2gx + 2fy + c = 0,
We get g = 0, f = 0, c = -9
Given point P(x₁, y₁) = (1, 1)
∴ The equation of chord of contact is S1 = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(1) + 0(x + 1) + 0(y + 1) – 9 = 0
⇒ x + y – 9 = 0

Question 46.
Find the pole of ax + by + c = 0 with respect to the circle x² + y² = r². [(AP) May ’16]
Solution:
Given the equation of the circle is x² + y² = r²
Let P(x₁, y₁) be the pole of ax + by + c = 0 …….(1)
The polar of P w.r. t the circle x² + y² = r² is S₁ = 0
xx₁ + yy₁ – r² = 0 ……(2)
Now (1) and (2) represent the same line

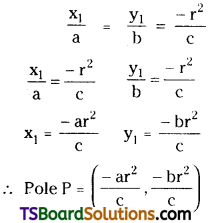
Question 47.
Discuss the relative position of the pair of circles (x – 2)² + (y + 1)² = 9, (x + 1)² + (y – 3)² = 4.
Solution:
Given equations of the circles are
(x – 2)² + (y + 1)² = 9 ……..(1)
(x + 1)² + (y – 3)² = 4 ………(2)
For circle (1),
Centre c₁ = (2, -1); radius r₁ = 3
For circle (2),
Centre c₂ = (-1, 3); radius r₂ = 2
c₁c₂ = \(\sqrt{(2+1)^2+(-1-3)^2}\)
= \(\sqrt{9+16}\)
= √25
= 5
Now r₁ + r₂ = 3 + 2 = 5
∴ c₁c₂ = r₁ + r₂
∴ The given circles touch each other externally.

Question 48.
Find the number of common tangents that exist for the pair of circles x² + y² = 4, x² + y² – 6x – 8y + 16 = 0. (May ’93)
Solution:
Given equations of the circles are
x² + y² = 4 ……(1)
x² + y² – 6x – 8y + 16 = 0 ………(2)
For circle (1),
centre, C₁ = (0, 0); Radius, r₁ = 2
For circle (2),
centre, C₂ = (3, 4)
Radius, r₂ = \(\sqrt{(-3)^2+(-4)^2-16}\) = √9 = 3
C₁C₂ = \(\sqrt{(0-3)^2+(0-4)^2}\) = √25 = 5
Now, r₁ + r₂ = 3 + 2 = 5
∴ C₁C₂ = r₁ + r₂
∴ The given circles touch each other externally.
∴ No. of common tangents = 3

Question 49.
Find the equation of the circle with centre (-7, -3) and radius ‘4’. (May ’93)
Solution:
Given centre, C(h, k) = (-7, -3)
radius, r = 4
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x + 7)² + (y + 3)² = 4²
⇒ x² + 49 + 14x + y² + 9 + 6y = 16
⇒ x² + y² + 14x + 6y + 42 = 0

Question 50.
Find the equation of the circle passing through (2, -1) having the centre at (2, 3).
Solution:
Given centre, C(h, k) = (2, 3)
Let, the given point A(2, -1)
Since, A(2, -1) is a point on the circle
∴ Radius, r = CA = \(\sqrt{(2-2)^2+(-1-3)^2}\)
= \(\sqrt{0+(-4)^2}\)
= √16
= 4
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = 4²
⇒ x² + 4 – 4x + y² + 9 – 6y = 16
⇒ x² + y² – 4x – 6y – 3 = 0

Question 51.
Find the values of a, b if ax² + bxy + 3y² – 5x + 2y – 3 = 0 represents a circle. Also, find the radius and centre of the circle.
Solution:
Given equation is ax² + bxy + 3y² – 5x + 2y – 3 = 0 …….(1)
Comparing the equation (1) with ax² + 2hxy + by² + 2gx + 2fy + c = 0
We get a = a,
2h = b ⇒ h = \(\frac{b}{2}\)
b = 3
Now, equation (1) represents a circle, then
(i) a = b ⇒ a = 3
(ii) h = 0 ⇒ \(\frac{b}{2}\) = 0 ⇒ b = 0
The equation of the circle is 3x² + 3y² – 5x + 2y – 3 = 0
⇒ \(x^2+y^2-\frac{5}{3} x+\frac{2}{3} y-1=0\)
Comparing the above equation with x² + y² + 2gx + 2fy + c = 0, we get

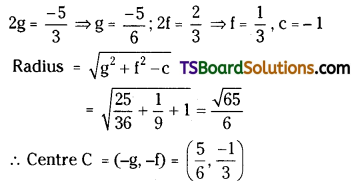
Question 52.
Find the equation of the circle with (4, 2), (1, 5) as ends of a diameter. [(AP) Mar. ’19]
Solution:
Let A(x₁, y₁) = (4, 2) and B(x₂, y₂) = (1, 5) are the two given points.
∴ The equation of the required circle is (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ (x – 4) (x – 1) + (y – 2) (y – 5) = 0
⇒ x² – 4x – x + 4 + y² – 5y – 2y + 10 = 0
⇒ x² + y² – 5x – 7y + 14 = 0

Question 53.
Show that A(3, -1) lies on the circle x² + y² – 2x + 4y = 0. Also, find the other end of the diameter through A. (May ’99, ’95, ’91)
Solution:
Given equation of the circle is x² + y² – 2x + 4y = 0 ……(1)
Given point A = (3, -1)
Now substituting the point A (3, -1) in equation (1)
(3)² + (-1)² – 2(3) + 4 (-1) = 0
9 + 1 – 6 – 4 = 0
10 – 10 = 0
0 = 0
∴ The point A(3, -1) lies on the circle x² + y² – 2x + 4y = 0.

Comparing the equation with x² + y² + 2gx + 2fy + c = 0
We get g = -1, f = 2, c = 0
Centre C = (-g, -f) = (1, -2)
Let B = (x, y) be the other end of the diameter.
Since ‘C’ is the midpoint of \(\overline{\mathrm{AB}}\) then
C = \(\left[\frac{\mathrm{x}_1+\mathrm{x}_2}{2}, \frac{\mathrm{y}_1+\mathrm{y}_2}{2}\right]\)
(1, -2) = \(\left(\frac{3+\mathrm{x}}{2}, \frac{-1+\mathrm{y}}{2}\right)\)
\(\frac{3+x}{2}\) = 1
⇒ 3 + x = 2
⇒ x = 2 – 3
⇒ x = -1
\(\frac{-1+\mathrm{y}}{2}\) = -2
⇒ -1 + y = -4
⇒ y = -4 + 1
⇒ y = -3
∴ Other end of the diameter B(x, y) = (-1, -3)

Question 54.
Find the equation of the circle passing through (3, -4) and concentric with x² + y² + 4x – 2y + 1 = 0.
Solution:
Given equation of the circle is x² + y² + 4x – 2y + 1 = 0
The equation of the circle concentric with the given circle is
x² + y² + 4x – 2y + k = 0 ……..(1)
The circle (1) passes through (3, -4) then
(3)² + (-4)² + 4(3) – 2(-4) + k = 0
⇒ 9 + 16 + 12 + 8 + k = 0
⇒ 45 + k = 0
⇒ k = -45
∴ The equation of the required circle is x² + y² + 4x – 2y – 45 = 0

Question 55.
Find the lengths of the intercepts made by the circle x² + y² + 8x – 12y – 9 = 0 on coordinate axes.
Solution:
Given equation of the circle is x² + y² + 8x – 12y – 9 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = 4, f = -6, c = -9
Length of the intercept made on X-axis = \(2 \sqrt{\mathrm{g}^2-\mathrm{c}}\)
= \(2 \sqrt{(4)^2+9}\)
= 2√25
= 2(5)
= 10
Length of the intercept made on Y-axis = \(2 \sqrt{\mathrm{f}^2-\mathrm{c}}\)
= \(2 \sqrt{(-6)^2+9}\)
= 2√45
= 6√5

Question 56.
Find the power of the point (3, 4) with respect to x² + y² – 4x – 6y – 12 = 0.
Solution:
Given equation of the circle is x² + y² – 4x – 6y- 12 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we get
g = -2, f = -3, c = -12
Given point P(x₁, y₁) = (3, 4)
Power of (3, 4) is S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\)
= (3)² + (4)² + 2(-2) (3) + 2(-3) (4) – 12
= 9 + 16 – 12 – 24 – 12
= -23

Question 57.
Find the polar of (1, 2) with respect to x² + y² = 7. (Mar. ’95)
Solution:
Given equation of the circle is x² + y² – 7 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we get
g = 0, f = 0, c = -7
Let the given point P(x₁, y₁) = (1, 2)
The equation of polar of P(1, 2) w.r.t. the given circle is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(2) + 0(x + 1) + 0(y + 2) – 7 = 0
⇒ x + 2y – 7 = 0

Question 58.
Find the pole of the line 3x + 4y – 12 = 0 with respect to x² + y² = 24.
Solution:
Comparing 3x + 4y – 12 = 0 with the equation lx + my + n = 0, we get
l = 3, m = 4, n = -12
Comparing x² + y² = 24 with x² + y² = a²
we get a² = 24
∴ Pole = \(\left(\frac{-l \mathrm{a}^2}{\mathrm{n}}, \frac{-m \mathrm{a}^2}{\mathrm{n}}\right)\)
= \(\left(\frac{-3(24)}{-12}, \frac{-4(24)}{-12}\right)\)
= (6, 8)

Question 59.
Show that the points (-6, 1) and (2, 3) are conjugate points with respect to the circle x² + y² – 2x + 2y + 1 = 0. (Mar. ’96)
Solution:
Given equation of the circle is x² + y² – 2x + 2y + 1 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -1, f = 1, c = 1
Let the given points are P(x₁, y₁) = (-6, 1), Q(x₂, y₂) = (2, 3)
Now S₁₂ = x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c
= (-6)(2) + 1(3) – 1(-6 + 2) + 1(1 + 3) + 1
= 12 + 3 – (-4) + 1(4) + 1
= -12 + 3 + 4 + 4 + 1
= -12 + 12
= 0
Since S₁₂ = 0 then, the given points are conjugate w.r.t. the given circle.

Question 60.
Find the pair of tangents drawn from (0, 0) to x² + y² + 10x + 10y + 40 = 0. (Mar. ’94)
Solution:
Given equation of the circle is x² + y² + 10x + 10y + 40 = 0
Here g = 5, f = 5, c = 40
Let the given point P(x₁, y₁) = (0, 0)
The equation of the pair of tangents drawn from (0, 0) to x² + y² + 10x + 10y + 40 = 0 is \(\mathrm{S}_1^2\) = SS₁₁
⇒ (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c)² = (x² + y² + 2gx + 2fy + c) \(\left(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\right)\)
⇒ [x(0) + y(0) + 5(x + 0) + 5(y + 0) + 40]² = (x² + y² + 10x + 10y + 40) [0 + 0 + 2(5)(0) + 2(5)(0) + 40]
⇒ (5x + 5y + 40)² = (x² + y² + 10x + 10y + 40)(40)
⇒ 25(x + y + 8)² = (x² + y² + 10x + 10y + 40)(40)
⇒ 5(x² + y² + 64 + 2xy + 16y + 16x) = (x² + y² + 10x + 10y + 40) (8)
⇒ 5x² + 5y² + 320 + 10xy + 80y + 80x = 8x² + 8y² + 80x + 80y + 320
⇒ 3x² – 10xy + 3y² = 0

Question 61.
Find the equation to the pair of tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0.
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 2 = 0
Here, g = -3, f = 2, c = -2
Let, the given point P(x₁, y₁) = (3, 2)
∴ The equation of the pair of tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0 is SS₁₁ = \(\mathrm{S}_1^2\)
⇒ (x² + y² + 2gx + 2fy + c) \(\left(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{g}_1+2 \mathrm{fy} \mathrm{y}_1+\mathrm{c}\right)\) = (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c)²
⇒ (x² + y² – 6x + 4y – 2) [(3)² + (2)² + 2(-3)(3) + 2(2) (2) – 2] = [x(3) + y(2) – 3(x + 3) + 2(y + 2) + (-2)]²
⇒ (x² + y² – 6x + 4y – 2) (9 + 4- 18 + 8- 2) = (3x + 2y – 3x – 9 + 2y + 4 – 2)²
⇒ (x² + y² – 6x + 4y – 2) = (4y – 7)²
⇒ x² + y² – 6x + 4y – 2 = 16y² + 49 – 56y
⇒ x² – 15y² – 6x + 60y – 51 = 0

Question 62.
Find the pair of tangents from (4, 10) to the circle x² + y² = 25.
Solution:
Given the equation of the circle is x² + y² = 25
Here, g = 0, f = 0, c = -25
Let the given point P(x₁, y₁) = (4, 10)
The equation of the pair of tangents drawn from (4, 10) to x² + y² = 25 is SS₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + y² + 2gx + 2fy + c) \(\left(x_1^2+y_1^2+2 g x_1+2 f y_1+c\right)\) = [xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c]²
⇒ (x² + y² – 25)((4)² + (10)² + 2(0)(4) + 2(0)(10) – 25) = [x(4) + y(10) + 0(x + 4) + 0(y + 10) – 25]²
⇒ (x² + y² – 25) (16 + 100 – 25) = (4x + 10y – 25)²
⇒ (x² + y² – 25) (91) = 16x² + 100y² + 625 + 80xy – 500y – 200x
⇒ 91x² + 91y² – 2275 = 16x² + 100y² + 625 + 80xy – 500y – 200x
⇒ 75x² – 80xy – 9y² + 200x + 500y – 2900 = 0

Question 63.
Find the angle between the pair of tangents drawn from (1, 3) to the circle x² + y² – 2x + 4y – 11 = 0. [(TS) Mar. ’16]
Solution:
Given equation of the circle is x² + y² – 2x + 4y – 11 = 0

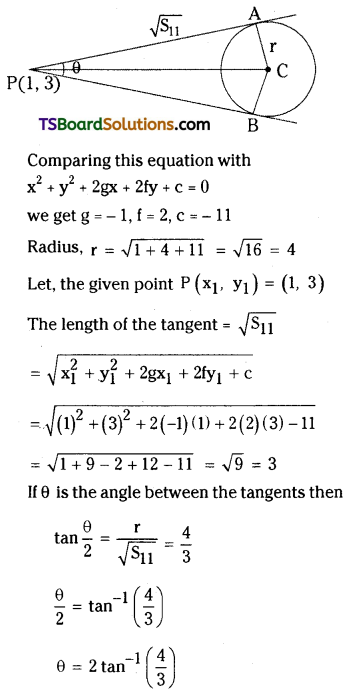
Question 64.
m Find the equation of a circle with centre (1, 4) and radius 5. [Mar. ’17 (AP)]
Solution:
Given centre C(h, k) = (1, 4)
radius r = 5
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x – 1)² + (y – 4)² = (5)²
⇒ x² + 1 – 2x + y² + 16 – 8y = 25
⇒ x² + y² – 2x – 8y – 8 = 0

Question 65.
Obtain the parametric equation of the circle 4(x² + y²) = 9. [Mar. ’17 (TS)]
Solution:
Given equation of the circle is 4(x² + y²) = 9
⇒ x² + y² = \(\frac{9}{4}\)
This is of the form x² + y² = r²
centre C = (h, k) = (0, 0)
radius r = \(\frac{3}{2}\)
∴ The parametric equations of the circle are
x = h + r cos θ = 0 + \(\frac{3}{2}\) cos θ = \(\frac{3}{2}\) cos θ
y = k + r sin θ = 0 + \(\frac{3}{2}\) sin θ = \(\frac{3}{2}\) sin θ
0 ≤ θ ≤ 2π

Question 66.
Find the centre and radius of the circle 3x² + 3y² + 6x – 12y – 1 = 0.
Solution:
Given equation of the circle is 3x² + 3y² + 6x – 12y – 1 = 0
⇒ x² + y² + 2x – 4y – \(\frac{1}{3}\) = 0 …….(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0, we get

Question 67.
Find the equation of the circle whose extremities of a diameter are (1, 2), (4, 6).
Solution:
Let A(x₁, y₁) = (1, 2) and B(x₂, y₂) = (4, 6) are the two given points.
∴ The equation of the required circle is (x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 1) (x – 4) + (y – 2) (y – 6) = 0
⇒ x² – 4x – x + 4 + y² – 6y – 2y + 12 = 0
⇒ x² + y² – 5x – 8y + 16 = 0

Question 68.
Find the number of common tangents to the circles x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0.
Solution:
Given equations of the circles are
x² + y² + 6x + 6y + 14 = 0 ……..(1)
x² + y² – 2x – 4y – 4 = 0 ………(2)
For the circle (1), centre, C₁ = (-3, -3)

Now, r₁ + r₂ = 2 + 3 = 5 = √25
∴ C₁C₂ > r₁ + r₂
∴ Number of common tangents = 4

Question 69.
Find the equation of the circle whose centre is (-1, 2) and which passes through (5, 6). [Mar. ’18 (TS)]
Solution:
Given centre c(h, k) = (-1, 2) and P(5, 6) be a point on the circle

Radius r = CP = \(\sqrt{(5+1)^2+(6-2)^2}\)
= \(\sqrt{36+16}\)
= √52
Equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x + 1)² + (y – 2)² = (√52)²
⇒ x² + 1 + 2x + y² + 4 – 4y = 52
⇒ x² + y² + 2x – 4y – 47 = 0

Question 70.
Write the parametric equations of the circle 2x² + 2y² = 7. [Mar. ’19 (TS)]
Solution:
Given the equation of the circle is 2x² + 2y² = 7
⇒ x² + y² = \(\frac{7}{2}\)
This is of the form x² + y² = r²
centre C = (h, k) = (0, 0)
radius r = \(\frac{\sqrt{7}}{\sqrt{2}}\)
∴ The parametric equations of the circle are
x = h + r cos θ = 0 + \(\frac{\sqrt{7}}{\sqrt{2}}\) cos θ = \(\frac{\sqrt{7}}{\sqrt{2}}\) cos θ
y = k + r sin θ = 0 + \(\frac{\sqrt{7}}{\sqrt{2}}\) sin θ = \(\frac{\sqrt{7}}{\sqrt{2}}\) sin θ
0 ≤ θ ≤ 2π

Question 71.
Prove that the equation of the circle with centre C(h, k) and radius r is (x – h)² + (y – k)² = r².
Solution:
Let P(x, y) be a point P lies in the circle then PC = r

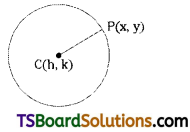
⇒ PC = r
⇒ \(\sqrt{(\mathrm{x}-\mathrm{h})^2+(\mathrm{y}-\mathrm{k})^2}\) = r
squaring on both sides
⇒ \(\left(\sqrt{(x-h)^2+(y-k)^2}\right)^2=r^2\)
⇒ (x – h)² + (y – k)² = r²
∴ The locus of P is (x – h)² + (y – k)² = r²
∴ The equation of the circle is (x – h)² + (y – k)² = r²

Question 72.
Prove that the equation of the circle with centre O(0, 0) and radius ‘r’ is x² + y² = r².
Solution:
Let P(x, y) be a point.
P lies in the circle then PO = r

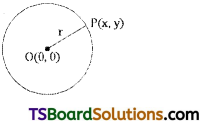
\(\sqrt{\mathrm{x}^2+\mathrm{y}^2}\) = r
Squaring on both sides
∴ x² + y² = r²

Question 73.
Find the equation of the circle with centre (cos α, sin α) and radius 1.
Solution:
Given centre C(h, k) = (cos α, sin α)
radius r = 1
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x – cos α)² + (y – sin α)² = (1)²
⇒ x² + cos²α – 2x cos α + y² + sin²α – 2y sin α = 1
⇒ x² + y² – 2x cos α – 2y sin α + 1 – 1 = 0
⇒ x² + y² – 2x cos α – 2y sin α = 0

Question 74.
Find the equation of the circle with centre \(\left(\frac{-1}{2},-9\right)\) and radius 5.
Solution:
Given centre C(h, k) = \(\left(\frac{-1}{2},-9\right)\)
radius r = 5
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ \(\left(\mathrm{x}+\frac{1}{2}\right)^2+(\mathrm{y}+9)^2=(5)^2\)
⇒ x² + x + \(\frac{1}{4}\) + y² + 81 + 18y – 25 = 0
⇒ x² + y² + x + 18y + 56 + \(\frac{1}{4}\) = 0
⇒ 4x² + 4y² + 4x + 72y + 1 + 224 = 0
⇒ 4x² + 4y² + 4x + 72y + 225 = 0

Question 75.
Find the equation of the circle with centre \(\left(\frac{5}{2}, \frac{-4}{3}\right)\) and radius 6.
Solution:
Given centre C(h, k) = \(\left(\frac{5}{2}, \frac{-4}{3}\right)\)
radius r = 6
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ \(\left(x-\frac{5}{2}\right)^2+\left(y+\frac{4}{3}\right)^2=(6)^2\)
⇒ \(x^2+\frac{25}{4}-5 x+y^2+\frac{16}{9}+\frac{8 y}{3}=36\)
⇒ \(\frac{36 x^2+225-180 x+36 y^2+64+96 y}{36}\) = 36
⇒ 36x² + 36y² – 180x + 96y + 289 = 1296
⇒ 36x² + 36y² – 180x + 96y – 1007 = 0

Question 76.
Find the equation of the circle with centre (1, 7) and radius \(\frac{5}{2}\).
Solution:
Given centre C(h, k) = (1, 7)
radius r = \(\frac{5}{2}\)
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x – 1)² + (y – 7)² = \(\left(\frac{5}{2}\right)^2\)
⇒ x² + 1 – 2x + y² + 49 – 14y = \(\frac{25}{4}\)
⇒ 4x² + 4 – 8x + 4y² + 196 – 56y = 25
⇒ 4x² + 4y² – 8x – 56y + 175 = 0

Question 77.
Find the equation of the circle with centre (0, 0) and radius 9.
Solution:
Given centre C(h, k) = (0, 0)
radius r = 9
∴ The equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x – 0)² + (y – 0)² = (9)²
⇒ x² + y² – 81 = 0

Question 78.
Find the centre and radius of the circle 2x² + 2y² – 3x + 2y – 1 = 0.
Solution:
Given equation of the circle is 2x² + 2y² – 3x + 2y – 1 = 0

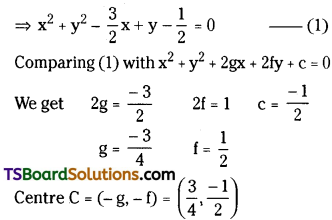
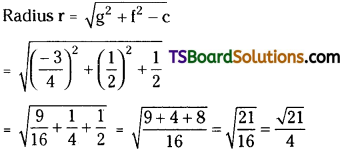
Question 79.
Find the equation of the circle having (7, -3), (3, 5) as the endpoints of a diameter.
Solution:
Let A(x₁, y₁) = (7, -3) and B(x₂, y₂) = (3, 5) are the two given points.
∴ The equation of the required circle is (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ (x – 7)(x – 3) + (y + 3)(y – 5) = 0
⇒ x² – 7x – 3x + 21 + y² – 5y + 3y – 15 = 0
⇒ x² + y² – 10x – 2y + 6 = 0

Question 80.
Find the equation of the circle having (1, 1), (2, -1) as the endpoints of a diameter.
Solution:
Let A(x₁, y₁) = (1, 1) and B(x₂, y₂) = (2, -1) are the two given points.
∴ The equation of the required circle is (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ (x – 1) (x – 2) + (y – 1) (y + 1) = 0
⇒ x² – 2x – x + 2 + y² – 1 = 0
⇒ x² + y² – 3x + 1 = 0

Question 81.
Find the equation of the circle having (0, 0), (8, 5) as the endpoints of a diameter.
Solution:
Let A(x₁, y₁) = (0, 0) and B(x₂, y₂) = (8, 5) are the two given points.
The equation of the required circle is (x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ (x – 0) (x – 8) + (y – 0) (y – 5) = 0
⇒ x² – 8x + y² – 5y = 0
⇒ x² + y² – 8x – 5y = 0

Question 82.
Obtain the parametric equations of the circle x² + y² – 4x – 6y – 12 = 0.
Solution:
Given the equation of the circle is
x² + y² – 4x – 6y – 12 = 0 ……..(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
We get 2g = -4 ⇒ g = -2
2f = -6 ⇒ f = -3
c = -12
Centre C(h, k) = (-g, -f) = (2, 3)
Radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(-2)^2+(-3)^2+12}\)
= √25
= 5
∴ The parametric equations of the circle are
x = h + r cos θ = 2 + 5 cos θ
y = k + r sin θ = 3 + 5 sin θ, 0 ≤ θ ≤ 2π.

Question 83.
Show that the power of a point P(x1, y1) w.r.t the circle S = 0 is S11.
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0 be the given circle and P(x₁, y₁) be any point in the plane, then centre C(-g, -f),

Question 84.
Prove that the length of the tangent drawn from an external point P(x₁, y₁) to the circle S = 0 is \(\sqrt{\mathbf{S}_{11}}\).
Solution:
Let S = x² + y² + 2gx + 2fy + c = 0 be the given circle

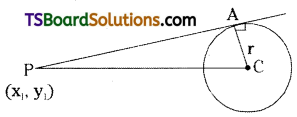
Centre C = (-g, -f) and Radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
Let the tangents drawn from P touches the circle at A.
∴ ∠PAC = 90°
⇒ OP² = PA² + CA²

Question 85.
Locate the position of the point P(1, 5) with respect to the circle x² + y² – 2x – 4y + 3 = 0.
Solution:
Given equation of the circle is x² + y² – 2x – 4y + 3 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
We get g = -1, f = -2, c = 3
Given point P(x₁, y₁) = (1, 5)
Now S₁₁ = \(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}\)
= (1)² + (5)² + 2(-1)(1) + 2(-2)(5) + 3
= 1 + 25 – 2 – 20 + 3
= 29 – 22
= 7
Since S₁₁ > 0, then the point P(1, 5) is outside the given circle.

Question 86.
Locate the position of the point P(4, 2) with respect to the circle 2x² + 2y² – 5x – 4y – 3 = 0.
Solution:
Given equation of the circle is 2x² + 2y² – 5x – 4y – 3 = 0
⇒ \(x^2+y^2-\frac{5}{2} x-2 y-\frac{3}{2}=0\)
Comparing this equation with x² + y² + 2gx + 2fy + c = 0

= 20 – 14 – \(\frac{3}{2}\)
= 6 – \(\frac{3}{2}\)
= \(\frac{9}{2}\) > 0
Since S₁₁ > 0, then the point P(4, 2) lies outside the circle.

Question 87.
Locate the position of the point P(2, -1) w.r.t the circle x² + y² – 2x – 4y + 3 = 0.
Solution:
Given equation of the circle is x² + y² – 2x – 4y + 3 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
We get g = -1, f = -2, c = 3
Given point P(x₁, y₁) = (2, -1)
Now S₁₁ = \(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\)
= (2)² – (-1)² + 2(-1)(2) + 2(-2)(-1) + 3
= 4 + 1 – 4 + 4 + 3
= 8 > 0
∵ S₁₁ > 0, then the point P(2, -1) lies outside the circle.

Question 88.
Locate the position of the point (2, 4) w.r.t the circle x² + y² – 4x – 6y + 11 = 0.
Solution:
Given equation of the circle is x² + y² – 4x – 6y + 11 = 0
Comparing this equation of the circle is x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -3, c = 11
Given point P(x₁, y₁) = (2, 4)
Now S₁₁ = \(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}\)
= (2)² + (4)² + 2(-2)(2) + 2(4)(-3) + 11
= 4 + 16 – 8 – 24 + 11
= 31 – 32
= -1 < 0
∵ S₁₁ < 0, then the point P(2, 4) lies inside the given circle.

Question 89.
Find the power of the point (5, -6) with respect to the circle x² + y² + 8x + 12y + 15 = 0.
Solution:
Given equation of the circle is x² + y² + 8x + 12y + 15 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 4, f = 6, c = 15
Point P(x₁, y₁) = (5, -6)
∴ The power of P(5, -6) w.r.t the given circle is S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{gx}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\)
S₁₁ =(5)² + (-6)² + 2(4)(5) + 2(6)(-6) + 15
= 25 + 36 + 40 – 72 + 15
= 116 – 72
= 44

Question 90.
Find the power of the point (2, 3) with respect to the circle x² + y² – 2x + 8y – 23 = 0.
Solution:
The given equation of the circle is x² + y² – 2x + 8y – 23 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -1, f = 4, c = -23
Point P(x₁, y₁) = (2, 3)
∴ The power of P(2, 3) w.r.t the given circle is S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{fy}_1+\mathrm{c}\)
S₁₁ = (2)² – (3)² + 2(-1)(2) + 2(4)(3) – 23
= 4 + 9 – 4 + 24 – 23
= 10

Question 91.
Find the power of the point (2, 4) with respect to the circle x² + y² – 4x – 6y – 12 = 0.
Solution:
The given equation of the circle is x² + y² – 4x – 6y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -3, c = -12
Point P(x₁, y₁) = (2, 4)
∴ The power of P(2, 4) w.r.t the given circle is S₁₁ = \(\mathrm{x}_1^2+\mathrm{y}_1^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{f} \mathrm{y}_1+\mathrm{c}\)
S₁₁ = (2)² + (4)² + 2(-2)(2) + 2(-3)(4) – 12
= 4 + 16 – 8 – 24 – 12
= -24

Question 92.
Find the length of tangent from P(-2, 5) to the circle x² + y² – 25 = 0.
Solution:
The given equation of the circle is x² + y² – 25 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 0, f = 0, c = -25
Point P(x₁, y₁) = (-2, 5)
∴ The length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

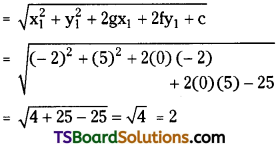
Question 93.
Find the equation of the tangent at (7, -5) of the circle x² + y² – 6x + 4y – 12 = 0.
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -3, f = 2, c = -12
The given point P(x₁, y₁) = (7, -5)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(7) + y(-5) – 3(x + 7) + 2(y – 5) – 12 = 0
⇒ 7x – 5y – 3x – 21 + 2y – 10 – 12 = 0
⇒ 4x – 3y – 43 = 0

Question 94.
Find the equation of the tangent at (3, 4) of the circle x² + y² – 4x – 6y + 11 = 0.
Solution:
The given equation of the circle is x² + y² – 4x – 6y + 11 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -3, c = 11
The given point P(x₁, y₁) = (3, 4)
The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(4) + (-2)(x + 3) – 3(y + 4) + 11 = 0
⇒ 3x + 4y – 2x – 6 – 3y -12 + 11 = 0
⇒ x + y – 7 = 0

Question 95.
Find the equation of the normal at (3, -4) of the circle x² + y² + x + y – 24 = 0.
Solution:
The given equation of the circle is x² + y² + x + y – 24 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = \(\frac{1}{2}\), f = \(\frac{1}{2}\), c = -24
The given point P(x₁, y₁) = (3, -4)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(-4) + \(\frac{1}{2}\)(x + 3) + \(\frac{1}{2}\)(y – 4) – 24 = 0
⇒ 3x – 4y + \(\frac{x}{2}+\frac{3}{2}+\frac{y}{2}\) – 2 – 24 = 0
⇒ 6x – 8y + x + 3 + y – 4 – 48 = 0
⇒ 7x – 7y – 49 = 0
⇒ x – y – 7 = 0
The slope of the tangent is m = \(\frac{-a}{b}=\frac{-1}{-1}\) = 1
The slope of the normal at P = \(\frac{-1}{\mathrm{~m}}=\frac{-1}{1}\) = -1
∴ The equation of the normal at P is
\(y-y_1=\frac{-1}{m}\left(x-x_1\right)\)
⇒ y + 4 = -1(x – 3)
⇒ y + 4 = -x + 3
⇒ x + y + 1 = 0

Question 96.
Find the equation of the normal at (3, 5) of the circle x² + y² – 10x – 2y + 6 = 0. [(AP) Mar. ’18]
Solution:
The given equation of the circle is x² + y² – 10x – 2y + 6 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -5, f = -1, c = 6
The given point P(x₁, y₁) = (3, 5)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(5) + (-5)(x + 3) – 1(y + 5) + 6 = 0
⇒ 3x + 5y – 5x – 15 – y – 5 + 6 = 0
⇒ -2x + 4y – 14 = 0
⇒ x – 2y + 7 = 0
The slope of the tangent at P is
m = \(\frac{-a}{b}=\frac{-1}{-2}\) = 1
The slope of the normal at
P = \(\frac{-1}{m}=\frac{-1}{\frac{1}{2}}\) = -2
∴ The equation of the normal at P(3, 5) is
\(y-y_1=\frac{-1}{m}\left(x-x_1\right)\)
⇒ y – 5 = -2(x – 3)
⇒ y – 5 = -2x + 6
⇒ 2x + y – 11 = 0

Question 97.
Find the equation of the normal at (1, 3) of the circle 3(x² + y²) – 19x – 29y + 76 = 0.
Solution:
The given equation of the circle is 3x² + 3y² – 19x – 29y + 76 = 0
⇒ \(x^2+y^2-\frac{19}{3} x-\frac{29}{3} y+\frac{76}{3}=0\)
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get \(\mathrm{g}=\frac{-19}{6}, \quad \mathrm{f}=\frac{-29}{6}, \mathrm{c}=\frac{76}{3}\)
The given point P(x₁, y₁) = (1, 3)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ \(x(1)+y(3)-\frac{19}{6}(x+1)-\frac{29}{6}(y+3)+\frac{76}{3}=0\)
⇒ 6x + 18y – 19x – 19 – 29y – 87 + 152 = 0
⇒ -13x – 11y + 46 = 0
⇒ 13x + 11y – 46 = 0
The slope of the tangent at P is
m = \(\frac{-a}{b}=\frac{-13}{11}\)
The slope of the normal at
P = \(\frac{-1}{\mathrm{~m}}=\frac{-1}{\frac{-13}{11}}=\frac{11}{13}\)
∴ The equation of the normal at P is
\(y-y_1=\frac{-1}{m}\left(x-x_1\right)\)
⇒ y – 3 = \(\frac{11}{33}\) (x – 1)
⇒ 13y – 39 = 11x – 11
⇒ 11x – 13y + 28 = 0

Question 98.
Find the equation of the normal at (1, 2) of the circle x² + y² – 22x – 4y + 25 = 0.
Solution:
The given equation of the circle is x² + y² – 22x – 4y + 25 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -11, f = -2, c = 25
The given point P(x₁, y₁) = (1, 2)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(3) – 11(x + 1) – 2(y + 2) + 25 = 0
⇒ x + 2y – 11x – 11 – 2y – 4 + 25 = 0
⇒ -10x + 10 = 0
⇒ x – 1 = 0
The slope of the tangent at P is m = \(\frac{-1}{0}\)
The slope of the normal at
P = \(\frac{-1}{m}=\frac{-1}{\frac{-1}{0}}=0\)
∴ The equation of the normal at P(1, 2) is
\(y-y_1=\frac{-1}{m}\left(x-x_1\right)\)
⇒ y – 2 = 0(x – 1)
⇒ y – 2 = 0

Question 99.
Find the equation of the circle with centre (-3, 4) and touching y-axis.
Solution:
Given centre C(h, k) = (-3, 4).
The equation of the y-axis is x = 0.

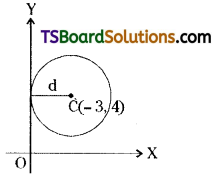
Since the required circle is touching the y-axis, the y-axis is the tangent to the required circle.
∴ Radius r = The perpendicular distance from the centre C(-3, 4) to the y-axis (x = 0)
∴ r = d = \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)
= \(\frac{|1(-3)+0(4)+0|}{\sqrt{(1)^2+(0)^2}}=\frac{|-3|}{1}\)
= 3
∴ The required equation of the circle is (x – h)² + (y – k)² = r²
⇒ (x + 3)² + (y – 4)² = (3)²
⇒ x² + 9 + 6x + y² + 16 – 8y = 9
⇒ x² + y² + 6x – 8y + 16 = 0

Question 100.
Find the equation of tangent and normal at (3, 2) of the circle x² + y² – x – 3y – 4 = 0. [(AP) May ’19]
Solution:
The given equation of the circle is x² + y² – x – 3y – 4 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = \(\frac{-1}{2}\), f = \(\frac{-3}{2}\), c = -4
The given point P(x₁, y₁) = (3, 2)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 6x + 4y – x – 3 – 3y – 6 – 8 = 0
⇒ 5x + y – 17 = 0
The slope of the tangent at P is
m = \(\frac{-5}{1}\) = -5
The slope of the normal at
P = \(\frac{-1}{m}=\frac{-1}{-5}=\frac{1}{5}\)
∴ The equation of the normal at P is
\(y-y_1=\frac{-1}{m}\left(x-x_1\right)\)
⇒ -2 = \(\frac{1}{5}\) (x – 3)
⇒ 5y – 10 = x – 3
⇒ x – 5y + 7 = 0

Question 101.
Find the equation of tangent and normal at (1, 1) of the circle 2x² + 2y² – 2x – 5y + 3 = 0.
Solution:
The given equation of the circle is 2x² + 2y² – 2x – 5y + 3 = 0
⇒ \(x^2+y^2-x-\frac{5}{2} y+\frac{3}{2}=0\) …..(1)
Comparing (1) with x² + y² + 2gx + 2fy + c = 0
We get \(\mathrm{g}=\frac{-1}{2}, \mathrm{f}=\frac{-5}{4}, \mathrm{c}=-\frac{3}{2}\)
The given point P(x₁, y₁) = (1, 1)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(1) – \(\frac{1}{2}\)(x + 1) – \(\frac{5}{4}\)(y + 1) + \(\frac{3}{2}\) = 0
⇒ 4x + 4y – 2x – 2 – 5y – 5 + 6 = 0
⇒ 2x – y – 1 = 0
The slope of the tangent at P is m = \(\frac{-2}{-1}\) = 2
The slope of the normal at P is \(\frac{-1}{\mathrm{~m}}=\frac{-1}{2}\)
∴ The equation of the normal at P is
\(y-y_1=\frac{-1}{m}\left(x-x_1\right)\)
⇒ \(y-1=\frac{-1}{2}(x-1)\)
⇒ 2y – 2 = -x + 1
⇒ x + 2y – 3 = 0

Question 102.
Show that the circle S = x² + y² + 2gx + 2fy + c = 0 touches the
(i) X-axis if g² = c
(ii) Y-axis if f² = c
Solution:
Given the equation of the circle is
S = x² + y² + 2gx + 2fy + c = 0
(i) The intercept made by S = 0 on X-axis = \(2 \sqrt{\mathrm{g}^2-\mathrm{c}}\)
Since, the circle touches the X-axis, then
\(2 \sqrt{\mathrm{g}^2-\mathrm{c}}\) = 0
⇒ \(\sqrt{g^2-c}\) = 0
⇒ g² – c = 0
⇒ g² = c

(ii) The intercept made by S = 0 on Y-axis is \(2 \sqrt{\mathrm{f}^2-\mathrm{c}}\)
Since, the circle touches the Y-axis, then
⇒ \(2 \sqrt{\mathrm{g}^2-\mathrm{c}}\)
⇒ \(\sqrt{f^2-c}\) = 0
⇒ f² – c = 0
⇒ f² = c

Question 103.
If the parametric values of two points A and B lying on the circle x² + y² – 6x + 4y – 12 = 0 are 30° and 60° respectively, then find the equation of the chord joining A and B.
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 12 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0

⇒ 2x – 6 + 2y + 4 = 5√3 + 5
⇒ 2x + 2y – 2 – 5 – 5√3 = 0
⇒ 2x + 2y – (7 + 5√3) = 0

Question 104.
Find the chord of contact of (0, 5) w.r.t the circle x² + y² – 5x + 4y – 2 = 0.
Solution:
Given equation of the circle is x² + y² – 5x + 4y – 2 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = \(\frac{-5}{2}\), f = 2, c = -2
Let, the given point P(x₁, y₁) = (0, 5)
∴ The equation of the chord of contact is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(0) + y(5) – \(\frac{5}{2}\)(x + 0) + 2(y + 5) – 2 = 0
⇒ 0 + 5y – \(\frac{5}{2}\)x + 2y + 10 – 2 = 0
⇒ 10y – 5x + 4y + 20 – 4 = 0
⇒ -5x + 14y + 16 = 0
⇒ 5x – 14y – 16 = 0

Question 105.
Find the chord of contact of (2, 5) w.r.t the circle x² + y² – 5x + 4y – 2 = 0.
Solution:
Given equation of the circle is x² + y² – 5x + 4y – 2 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = \(\frac{-5}{2}\), f = 2, c = -2
Let, the given point P(x₁, y₁) = (2, 5)
∴ The equation of the chord of contact is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(2) + y(5) – \(\frac{5}{2}\)(x + 2) + 2(y + 5) – 2 = 0
⇒ 2x + 5y – \(\frac{5}{2}\)x – 5 + 2y + 10 – 2 = 0
⇒ 2x – \(\frac{5}{2}\)x + 7y + 3 = 0
⇒ 4x – 5x + 14y + 6 = 0
⇒ -x + 14y + 6 = 0
⇒ x – 14y – 6 = 0

Question 106.
Show that the points (4, 2) and (3, -5) are conjugate points w.r.t the circle x² + y² – 3x – 5y + 1 = 0.
Solution:
Given equation of the circle is x² + y² – 3x – 5y + 1 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get \(\mathrm{g}=\frac{-3}{2}, \mathrm{f}=\frac{-5}{2}, \mathrm{c}=1\)
Let, the given point are A(x₁, y₁) = (4, 2), B(x₂, y₂) = (3, -5)
Now S₁₂ = x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0

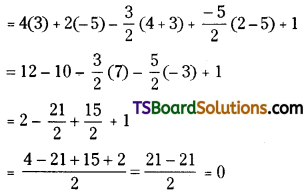
Since S₁₂ = 0, the given points are conjugate w.r.t the given circle.

Question 107.
Find the value of ‘k’ if the points (1, 3) and (2, k) are conjugate w.r.t the circle x² + y² = 35.
Solution:
Given the equation of the circle is x² + y² = 35
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 0, f = 0, c = -35
Let, the given points are A(x₁, y₁) = (1, 3), B(x₂, y₂) = (2, k)
Since the given points are conjugate, then S₁₂ = 0
⇒ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
⇒ 1(2) + 3(k) + 0(1 + 2) + 0(3 + k) – 35 = 0
⇒ 2 + 3k + 0 + 0 – 35 = 0
⇒ 3k – 33 = 0
⇒ 3k = 33
⇒ k = 11

Question 108.
Find the value of ‘k’ if the points (4, 2) and (k, -3) are conjugate points w.r.t the circle x² + y² – 5x + 8y + 6 = 0.
Solution:
Given equation of the circle is x² + y² – 5x + 8y + 6 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = \(\frac{-5}{2}\), f = 4, c = 6
Let, the given points are A(x₁, y₁) = (4, 2) and B(x₂, y₂) = (k, -3)
Since the given points are conjugate, then S₁₂ = 0
⇒ x₁x₂ + y₁y₂ + g(x₁ + x₂) + f(y₁ + y₂) + c = 0
⇒ 4(k) + 2(-3) – \(\frac{5}{2}\)(4 + k) + 4(2 – 3) + 6 = 0
⇒ 4k – 6 – \(\frac{20}{2}-\frac{5 \mathrm{k}}{2}\) – 4 + 6 = 0
⇒ \(\frac{-5 k}{2}\) + 4k – 14 = 0
⇒ \(\frac{-5 k+8 k-28}{2}\) = 0
⇒ 3k – 28 = 0
⇒ 3k = 28
⇒ k = \(\frac{28}{3}\)

Question 109.
Find the angle between the tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0.
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 2 = 0

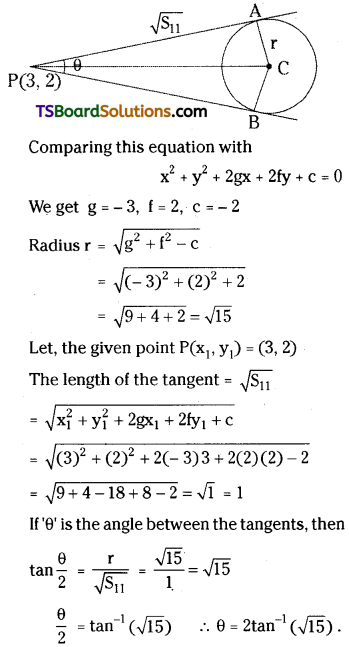
Question 110.
Discuss the relative position of the pair of circles x² + y² – 4x – 6y – 12 = 0, x² + y² + 6x + 18y + 26 = 0.
Solution:
Given equations of the circles are
x² + y² – 4x – 6y – 12 = 0 …….(1)
x² + y² + 6x + 18y + 26 = 0 ………(2)
for the circle (1), centre c₁ = (2, 3)

Now, r₁ + r₂ = 5 + 8 = 13
∴ c₁c₂ = r₁ + r₂
∴ The given circles touch each other externally.

Question 111.
Discuss the relative position of the pair of circles x² + y² – 2x + 4y – 4 = 0, x² + y² + 4x – 6y – 3 = 0.
Solution:
Given equations of the circles are
x² + y² – 2x + 4y – 4 = 0 …….(1)
x² + y² + 4x – 6y – 3 = 0 ………..(2)
For the circle (1), centre c₁ = (1, -2)

Question 112.
Find the number of possible common tangents that exist for the pairs of circles x² + y² + 6x + 6y + 14 = 0, x² + y² – 2x – 4y – 4 = 0.
Solution:
Given equations of the circles are
x² + y² + 6x + 6y + 14 = 0 ……..(1)
x² + y² – 2x – 4y – 4 = 0 ……….(2)
For the circle (1), Centre c₁ = (-3, -3)


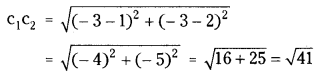
Now, r₁ + r₂ = 2 + 3 = 5 = √25
∴ c₁c₂ > r₁ + r₂
∴ Given circles, each circle lies completely outside the other.
∴ The number of common tangents = 4.

Question 113.
Find the number of possible common tangents that exist for the pairs of circles x² + y² – 4x – 2y + 1 = 0, x² + y² – 6x – 4y + 4 = 0.
Solution:
Given equations of the circles are
x² + y² – 4x – 2y + 1 = 0 ……..(1)
x² + y² – 6x – 4y + 4 = 0 ……….(2)
For the circle (1), Centre c₁ = (2, 1)

Now, |r₁ – r₂| = |2 – 3| = |-1| = 1
r₁ + r₂ = 2 + 3 = 5 = √25
∴ |r₁ – r₂| < c₁c₂ < r₁ + r₂
∴ The given circles intersect at two points.
∴ The number of common tangents = 2.

Question 114.
Find the number of possible common tangents that exist for the pairs of circles x² + y² – 4x + 2y – 4 = 0, x² + y² + 2x – 6y + 6 = 0.
Solution:
Given equations of the circles are
x² + y² – 4x + 2y – 4 = 0 ……..(1)
x² + y² + 2x – 6y + 6 = 0 ……..(2)
For the circle (1), Centre c₁ = (2, -1)


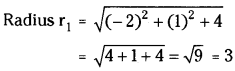
Now, r₁ + r₂ = 3 + 2 = 5
∴ c₁c₂ = r₁ + r₂
∴ The given circles touch each other externally.
∴ The number of common tangents = 3.

Question 115.
Find the number of possible common tangents that exist for the pairs of circles x² + y² + 4x – 6y – 3 = 0, x² + y² + 4x – 2y + 4 = 0.
Solution:
Given equations of the circles are
x² + y² + 4x – 6y – 3 = 0 ……..(1)
x² + y² + 4x – 2y + 4 = 0 ……….(2)
For the circle (1), Centre c₁ = (-2, 3)

Now, |r₁ + r₂| = |4 + 1| = 5
∴ c₁c₂ < |r₁ + r₂|
∴ In the given circles one circle lies completely inside the other.
∴ The number of common tangents = 0.

Question 116.
Find the equation of the pair of tangents from (10, 4) to the circle x² + y² = 25.
Solution:
The given equation of the circle is x² + y² = 25.
Here g = 0, f = 0, c = -25
Let, the given point P(x₁, y₁) = (10, 4)
∴ The equation of the pair of tangents drawn from (10, 4) to the circle x² + y² = 25 is
SS₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + y² + 2gx + 2fy+ c) \(\left(\mathrm{x}_1{ }^2+\mathrm{y}_1{ }^2+2 \mathrm{g} \mathrm{x}_1+2 \mathrm{fy}_1+\mathrm{c}\right)\) = (xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c)²
⇒ (x² + y² – 25) [(10)² + (4)² + 2(0)(10) + 2(0)(4) – 25] = [x(10) + y(4) + 0(x + 10) + 0(y + 4) – 25]²
⇒ (x² + y² – 25) (100 + 16 – 25) = (10x + 4y – 25)²
⇒ (x² + y² – 25) (91) = (10x + 4y – 25)²
⇒ 91x² + 91y² – 2275 = 100x² + 16y² + 625 + 80xy – 200y – 500x
⇒ 9x² + 80xy – 75y² – 500x – 200y + 2900 = 0