Mahesh

Here students can locate TS Inter 2nd Year Physics Notes 4th Lesson Electric Charges and Fields to prepare for their exam.

TS Inter 2nd Year Physics Notes 4th Lesson Electric Charges and Fields

→ Electrical charges given to conductors will flow from one end to other end. Charges moving through conductors leads to flow of current.

→ Electrical charges are two types

• positive charge,
• negative charge.

→ In the process of electrification we will remove or add electrons to substances with some techniques. Substance that looses electrons will become positive substance that gains electrons will become negative.

→ Quantisation of charge: Electric charge ‘Q ’ on a substance is an integral multiple of fundamental charge of electron, i.e., Q = ne. It is called Quantisation of charge.

→ Law of conservation of charge : The total charge of an isolated system is always con-stant. i.e., charge can not be created or des-troyed. This is known as “law of conservation of charge”.

→ Charge on electron e = 1.602 × 10^-19 C it is taken as fundamental charge.

→ Coulomb’s Law:
Force attraction (or) repulsion between the charges is proportional to product of charges and inversely proportional to the square of the distance between them.
∴ From Coulomb’s law F ∝ q₁q₂ and F ∝ 1/r²
F ∝ \(\frac{q_1 q_2}{r^2}\) (OR) F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
Where \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ N-m² / C² is a constant.
ε₀ is permittivity of free space.
Its value is 8.85 × 10^-12 farad/metre.

→ Force on a given charge (q) due to multiple charges is the vector sum of all the forces acting on the given charge.
\(\overline{\mathrm{F}_{\mathrm{R}}}=\overline{\mathrm{F}}_1+\overline{\mathrm{F}}_2+\overline{\mathrm{F}}_3\) ……….
Where F₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q^q q_2}{r_1^2}\) etc
Note : To find resultant force we must use principles of vector addition i.e., parallelogram law or triangle law.

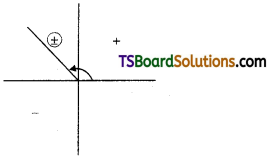
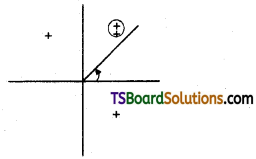
→ Electric field : Every charged particle (q) will produce an electric field everywhere in the surrounding. It is a vector. It follows inverse square law.

→ Intensity of electric field (or) electric field strength (E̅) : Intensity of electric field or electric field at a point in space is the force experienced by a unit positive charge placed at that point.
F = Eq (or) E = (F/q), SI unit: Vm^-1

→ Electric field lines of force : Electric field lines represent electric field E due to a charge ‘q’ in a pictorial manner. When E is strong field lines are move nearer or crowded. In a weak field electric field lines are less dense.

→ Electric flux (Φ): The number of electric field line passing through unit area placed normal to the field at a given point is called “electric flux”. It is a measure for the strength of electric field at that point.

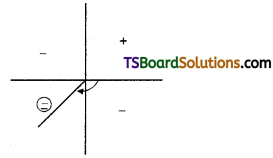
→ Electric dipole: Two equal and opposite charges separated by some distance will constitute an “electric dipole”.

→ Dipole moment (p̅): The product of one of the charge in dipole and separation between the charges is defined as “dipole moment (P̅)”.
Dipole moment (p̅) = q. 2a (or) p = 2aq
It is a vector. It acts along the direction of -q to q.
Unit: coulomb – metre.

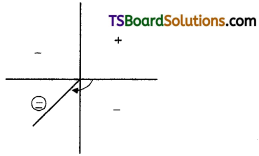
→ Dipole in a uniform electric field : Let an electric dipole is placed in an electric field of intensity E. Then F = Eq
Torque on dipole τ = p̅ x E̅
Let p̅ and E̅ are in the plane of the paper then torque τ will act perpendicularly to the plane of the paper.

→ Linear charge density (λ) :
It is defined as the ratio of charge (Q) to length of the conductor (L).
Linear charge density
λ = \(\frac{\text { Charge }}{\text { Length }} \frac{(\mathrm{Q})}{(\mathrm{L})}\)
⇒ λ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{L}}\)
Unit: Coulomb / metre.

→ Surface charge density (σ) : W
It is defined as the ratio of charge (Q) to surface area of (A) of that conductor.
Surface charge density
σ = \(\frac{\text { Charge }}{\text { Area }} \frac{(\mathrm{Q})}{(\mathrm{A})}\)
⇒ σ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{A}}\)
Unit: Coulomb / metre²

→ Volume charge density (ρ):
It is defined as the ratio of charge on the conductor ‘Q’ to volume of the conductor.
Volume charge density
ρ = \(\frac{\text { Charge }}{\text { Volume }} \frac{(Q)}{(V)}\)
⇒ ρ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{V}}\)
Unit: Coulomb / m³.

→ Gauss law : The total electrical flux (Φ) through a closed surface (s) is 1/ε₀ times more than the total charge (Q) enclosed by that surface.
From Gauss law (Φ) = \(\frac{1}{\varepsilon_0}\) Q

→ Important conclusions from Gauss’s law:

• Gauss law is applicable to any closed surface irrespective of its shape.
• The term Q refers to sum of all the charges inside the gaussian surface.
• A gaussian surface is that surface for which we choosed to apply gauss law.
• It is not necessary to consider any charges out side the gaussian surface to find the flux (Φ) coming out of it.
• Gauss law is very useful in the calculations to find electric field when the system (gaussian surface) has some symmetry.

→ Charge Q = ne. Where e = charge on electron = 1.6 × 10^-19 C.

→ Force between two charges F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)

→ Force between multiple charges : In a system of charges say q₁ q₂, q₃ ………. q_n.
Force on charge qj is say F₁ = F₁₂ + F₁₃ + F₁₄ ………….. F_1n
(OR) Total force on q₁ say
F₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{r_{21}^2}+\frac{q_1 q_3}{r_{13}^2}+\ldots . .+\frac{q_1 q_n}{r_{1 n}^2}\right]\)

→ Electric field due to a point charge q’ at a point r is E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}^2}\) (OR) E̅ = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}^2}\)r̅

→ Electric flux Φ = E.Δs = E Δs cos θ.
Where θ is the angle between electric field E̅ and area vector Δs .

→ Dipole moment p = q.2a. Where q is one of the charge on dipole and ‘2a’ is separation between the charges.

→ Electric field at any point on the axis of a dipole
E_axial = \(\frac{\mathrm{q}}{4 \pi \varepsilon_0} \frac{4 \mathrm{ar}}{\left[\mathrm{r}^2-\mathrm{a}^2\right]^2}=\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{pr}}{\left(\mathrm{r}^2-\mathrm{a}^2\right)^2}\)
where r > > a then E_axial = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{p}}{\mathrm{r}^3}\)
When r is the distance of given point from centre of dipole.

→ Electric field of any point on the equatorial line of a dipole.
E_eq = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{qa}}{\left[\mathrm{r}^2+\mathrm{a}^2\right]^{3 / 2}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{p}}{\left[\mathrm{r}^2+\mathrm{a}^2\right]^{3 / 2}}\)
When r >> a then E_eq = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{p}}{\mathrm{r}^3}\)
Note : E_axial and E_eq will act along the line joining the given point ’p’ and centre of dipole ‘O’.

→ Torque on a dipole when placed in a uniform electric field E is τ̅ = p̅ x E̅ = pE sin θ.
Where θ is the angle between P̅ and E̅.

→ Charge distribution on conductors:
Charge (Q) given to a conductor will uniformly spread on the entire conductor.
(a) Linear charge density λ = \(\frac{\text { Charge }}{\text { Length }} \frac{\mathrm{Q}}{\mathrm{L}}\) unit: C/m
(b) Surface charge density σ = \(\frac{\text { Charge }}{\text { Surface area }} \frac{Q}{A}\) unit / C/m²
(c) Volume charge density ρ = \(\frac{\text { Charge }}{\text { Volume }} \frac{Q}{V}\) unit: C/m³

→ Gauss’s law : The total electric flux (Φ) coming out of a closed surface is \(\frac{1}{\varepsilon_0}\) times greater than the total charge (Q) enclosed by that surface.
Φ = \(\frac{Q}{\varepsilon_0}\)

→ Electric field due to an infinitely long straight uniformly charged wire E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)n̅.
(∵ n̅ = 1) or, E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)

→ Field due to a uniformly charged infinite plane sheet is E = \(\frac{\sigma}{2 \varepsilon_0}\)n̅.
or. E = \(\frac{\sigma}{2 \varepsilon_0}\), (∵ n̅ = 1)

→ Field due to a uniformly charged thin spherical shell:
(a) At any point out side the shell is
E = \(\frac{\mathrm{Q}}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
(b) Inside the shell electric field E = 0.

Here students can locate TS Inter 2nd Year Physics Notes 3rd Lesson Wave Optics to prepare for their exam.

TS Inter 2nd Year Physics Notes 3rd Lesson Wave Optics

→ Huygens principle: Each point on the wave-front is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave. These wave lets emanating from the wavefront are usually referred to as secondary wavelets.
From Huygens principle every wave is a secondary wave to the preceding wave.

→ Wavefront: The locus of points which oscillate in phase is called “wavefront”.
(OR)
A wavefront is defined as a surface of constant phase.

→ Plane wave: Generally wavefront is spherical in nature when radius of sphere is very large. A small portion of spherical wave can be treated as plane wave.

→ Geometrical optics: It is a branch of optics in which we are completely neglects the finiteness of the wavelength is called geometrical optics. A ray of light is defined as the path of energy propagation. In this concept wavelength of light is tending to zero.

→ Snell’s law of refraction: Let nj and n2 are the refractive indices of the two media and i’ and ‘r’ are angle of incidence and angle of refraction then
n₁ sin i = n₂ sin r. This relation is called Snell’s law.
From Snell’s law for a given pair of media sin i / sin r = n₂ / n₁ is constant also called refractive index of the medium. Where nj is air or vacuum.

→ Critical angle (I_c): It is define as the angle of incidence in denser medium i for which angle of refraction in rarer medium r = 90°.
μ = \(\frac{1}{\sin c}\)
i. e, when r = 90° then i = C in denser medium.

→ Doppler’s effect in light: When there is relative motion between source and obser¬ver then there is a change in frequency of light received by the observer.

→ Red shift: If the source moves away from the, observer then frequency measured by observer is less (i.e., wavelength increases) as a result wavelength of received light moves towards red colour. This is known as “red shift”.

→ Blue shift: When source of light is approach¬ing the observer frequency of light received increases, (i.e., wavelength of light decreases.) As a result wavelength of received light will move towards blue colour. This is known as “blue shift”.

→ Superposition principle: According to super¬position principle at a particular point in the medium the resultant displacement produced by a number of waves is the vector sum of the displacements produced by each of the waves.

→ Coherent soures: Two sources are said to be coherent when the phase difference pro¬duced by each of two waves does not change with time.
Note: For a non – coherent waves the phase difference between them changes with time.

→ Interference: Interference is based on the superposition principle. According to which at a particular point in the medium the resultant displacement produced by a number of waves is the vecotor sum of displacements produced by each of the wave.
Note: In light when two coherent waves are superposed we will get dark and bright bands.

→ Constructive interference Or bright band:
When two coherent waves of path difference λ /2 or its integral multiples or a phase difference of or integral multiples of 2π are superposed on one another then the displacements of the two waves are in phase and intensity of light is 4I₀ where I₀ is intensity of each wave.
Condition, for constructive interference
is path difference = nλ or Φ = 0, 2π, 4π ………….. etc i.e., even multiples of π.

→ Destructive interference or dark band:
When two coherent waves of path difference \(\frac{\lambda}{2}\) or (n + \(\frac{1}{2}\)) λ or phase difference of \(\frac{\pi}{2}\) or odd multiples of \(\frac{\pi}{2}\) superposed at a given point then their displacements are out of phase and resultant intensity its is zero. This is called dark band.
For dark band to from path difference
= (n + \(\frac{1}{2}\)) λ (OR)
phase difference Φ = π, 3π, 5π …. odd multiples of n.

→ Diffraction: Bending of light rays at sharp edges (say edge of blade) is called”diffraction”.
As a result of diffraction we can see dark and bright bands close to the region of geometrical shadow.

→ Resolving power of Telescope:
Resolving power of telescope Δθ = \(\frac{0.61 \lambda}{\mathrm{a}}\)
Where 2a is aperture or vertical height (dia-meter) of lens used:
Resolving power of telescopes is its ability to show two distant object clearly when angular separation between them is Δθ.
When Δθ is less then resolving power of that telescope is high.
From above equation to increase resolving power of telescope its aperture or diameter of lens used must be high.

→ Resolving power of microscope:
The resolving power of the microscope is given by the reciprocal of the minimum separation of two points seen as distinct.
Minimum distance d_min = \(\frac{1.22 \lambda}{2 n \sin \beta}\), The term n sin β is called numerical aperture.
Resolving power of microscope = \(\frac{2 \mathrm{n} \sin \beta}{1.22 \lambda}\)
Note: The resolving power of microscope increases if refractive index n is high. In oil immersion objectives the lenses are placed in a transparent oil with refractive index close to that of objective lens to increase magnification.

→ Fresnel distance: The term z = a²/ λ is called fresnel distance.
In explaining the spreading of beam due to diffraction we will use the equation z = a²/ λ,
Where after travelling a distance z\(\frac{\lambda}{\mathrm{a}}\) size of beam is comparable to size of slit or hole ‘a’.
Note: When we are travelling from aperture to screen a distance z then width of diffrated beam z\(\frac{\lambda}{\mathrm{a}}\) is equals to aperture a’.
Beyond this distance ‘z’ divergence of the beam of width ‘a’ becomes significant. When distances are smaller than z spreading due to diffraction is small when compared with size of beam.

→ Polarisation: If is a process in which vib-rations of electric vectors of light are made ot oscillate, in a single direction.

→ Polaroids: A polaroid consists of a long chain of molecules aligned in a particular direction.

→ Malus’ Law: Let two polariods say P₁ and P₂ are arranged with some angle ‘θ’ between their axes. Then intensity of light coming
I = I₀ cos²θ
where I₀ is intensity of polarised light after passing through 1st polaroid P₁. This is known as Malus Law.

→ Uses of Polaroids: Polaroids are used

• to control intensity of light.
• They are used in photography,
• polaroids are used in sunglasses and in window panes.

→ Unpolarised light: In an unpolarised light electric vectors can vibrate in 360° direc¬tion perpendicular to direction of propaga¬tion. All these electric vectors can be grouped into two groups.

• Dot components they are vibrating perpendicular to the plane of the paper.
• Arrow components ‘↔’ i.e., their plane of vibration is along the plane of the paper.
  Thus an unploarised light can be shown as a group of dot components and arrow components.

→ Polorisation by scattering: The sky appears blue due to scattering of light. The light coming from clear blue portion of sky is made to pass through a polariser when it is rotated the intensity of light coming from polariser is found to be changing. Which shows that the scattered light consists of polarised light.

→ Polarisation by reflection:

• When unpolarised light falls on the boundary layer sepa-rating two transparent media the reflected light is found to be partially polarised. The amount of polarisation depends on angle of incidence i.
• It is found that when reflected ray and refracted ray are perpendicular the reflected ray is found to be totally plane polarised. The angle of incidence at this stage is known as Brewster angle.

→ Brewster’s angle: When reflected ray and refracted ray are mutually perpendicular then reflected ray is plane polarised. This particular angle of incidence i_B for which the reflected ray is plane polarised is called Brewster angle.

Explanation:
At Brewster angle i_B + r = \(\frac{\sin \mathrm{i}_{\mathrm{B}}}{\sin \mathrm{r}}=\frac{\sin \mathrm{i}_{\mathrm{B}}}{\sin \left(\pi / 2-\mathrm{i}_{\mathrm{B}}\right)}\)
n (OR) μ = \(\frac{\sin \mathrm{i}_{\mathrm{B}}}{\sin \mathrm{r}}=\frac{\sin \mathrm{i}_{\mathrm{B}}}{\sin \left(\pi / 2-\mathrm{i}_{\mathrm{B}}\right)}\)
= \(\frac{\sin \mathrm{i}_{\mathrm{B}}}{\cos \mathrm{i}_{\mathrm{B}}}\) = tani_B (OR) μ = tan i_B
∴ The tangent of Brewster’s angle tan (i_g) is equals to refractive index, i.e., μ = tan i_B.
Note: Refractive index can be shown by the symbol μ or n.

→ From the super position principle the resultant displacement is y = y₁ + y₂.
For constructive interference (bright band) y = y₁ + y₂) ; Intensity I = (y₁ + y₂)²
For destructive interference (dark band) y = y₁ ~ y₂; Intensity I = (y₁ – y₂)²

→ In interference, the resultant intensity
I = 4I₀ cos²\(\frac{\phi}{2}\) (Where I₀ is maximum intensity)
Resultant phase θ = \(\frac{\phi}{2}\) (Where Φ is initial phase difference)

→ Condition for formation of bright band is
(a) Path difference x = mλ, where m = 0,1, 2 ………….. etc.
(b) Phase difference Φ = 0, 2π ………… even multiples of π.

→ Condition for formation of dark band
(a) Path difference x = \(\frac{λ}{2}\) and odd multiples
(b) Phase difference Φ = π, 3π, 5π, ………….. odd multiples of n.

→ Relation between path difference (x) and
phase difference (Φ) is λ = \(\frac{\lambda}{2 \pi}\). Φ

→ Fringe with β = \(\frac{\lambda L}{\mathrm{~d}}\); Angular fringe width \(\frac{\beta}{L}=\frac{\lambda}{d}\)

→ Distance of mth bright band from central bright band is x₂ = \(\frac{\mathrm{m} \lambda \mathrm{L}}{\mathrm{d}}\)

→ Distance of m dark band from central dark band x₂ = \(\left(m+\frac{1}{2}\right) \lambda \frac{L}{d}\)

→ For two waves with intensities I and 12 with phase 4 resultant intensity
I = I₁ + I₂ + 2\(\sqrt{I_1 I_2}\)cos Φ

→ When a glass plate of thickness (t) is introduced in the path of one light wave then interference fringes will shift. Thickness glass plate t = \(\frac{m \lambda}{(\mu-1)}\)
m = number of fringes shifted;
λ = wavelength of light used.

→ When unpolarized light of intensity I, passes through a polarizer Intensity of emergent light I = \(\frac{\mathrm{I}_0}{2}\)

→ When polarized light falls on a polarizer with an angle θ to the axis then Intensity of refracted light I = I₀cos²θ

→ If polarized light falls on 1st polarIzer with an angle θ, and angle between the axes of given two polarizers is θ then intensity of light coming out of 2nd polarlzer I = I₀cos²θ₁cos²θ₂

→ For polarizatIon through reflection wIth Brewster angle i_B then μ or n = tan i_B

→ In diffraction radIus of central bright region
r₀ = \(\frac{1.22 \lambda \mathrm{f}}{2 \mathrm{a}}=\frac{0.61 \lambda \mathrm{f}}{\mathrm{a}}\)

→ ResolvIng power of telescope Δθ = \(\frac{0.61 \lambda}{\mathrm{a}}\)
Where Δθ Is the minimum angular separation between two distant objects.

→ Resolving power of microscope
d_min = \(=\frac{1.22 \mathrm{f} \lambda}{\mathrm{D}}=\frac{1.22 \lambda}{2 \tan \beta}=\frac{1.22 \lambda}{2 \sin \beta}=\frac{1.22 \lambda}{2 \mathrm{n} \sin \beta}=\frac{1.22 \lambda}{2 \mathrm{~N} \cdot \mathrm{A}}\)
Where d_min is the minimum separation required between two points in object.
N.A is numerical aperture (n sin β)
β is the angle subtended by the object at object lens.

→ Fresnel distance z = \(\frac{\mathrm{a}^2}{\lambda}\) Where ‘a’ is size of hole or slit.

Here students can locate TS Inter 2nd Year Physics Notes 2nd Lesson Ray Optics and Optical Instruments to prepare for their exam.

TS Inter 2nd Year Physics Notes 2nd Lesson Ray Optics and Optical Instruments

→ In ray optics, light will travel from one point to another point along a straight line. The path is called a “ray of light”. A bundle of such rays is called “a beam of light”.

→ Laws of reflection:

• Angle of reflection is equals to angle of incidence (r = i).
• The incident ray, the reflected ray and normal to the reflecting surface lie in the same plane.

→ Spherical mirrors:

• Pole (P): The geometrical centre of spherical mirror is called ‘pole ‘P’.”
• Principal axis: The line joining the pole (P) and centre of curvature ‘C’ of a spherical mirror is known as “principal axis”. Principal focus: For mirrors, after reflection a parallel beam of light w.r.to principal axis will converge or appears to diverge from a point on principal axis. This point is called “principal focus” ‘F’.
• Focal length (f): Distance between principal focus and pole of mirror or centre of lens is called “focal length”.

In spherical mirrors:

• Focal length of concave mirror is positive.
• Focal length of convex mirror is ve1.
• Relation between radius of curvature of mirror R and focal length f is R = 2f

→ Cartesian sign convention:

• All distances must be measured from the pole of the mirror or the optical centre of lens.
• The distances measured along the direction of the incident ray are taken as positive and the distances measured against the direction of incident ray are taken as negative.
• Distances measured above the principal axis of mirror (or) lens are taken as positive. The distances measured below are taken as ve’.

→ Mirror equation = \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)

→ Linear Magnification (m): The ratio of height of image (ht) to height of object (hj is called “linear magnification”. Linear magnification (m) = \(\frac{\mathbf{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}}=\frac{-\mathrm{v}}{\mathbf{u}}\)

→ Refraction: The bending nature of light rays at refracting surface while travelling from one medium to another medium.

→ Laws of refraction:

• The incident ray, the refracted ray and normal to the interface at the point of incidence all lie in the same plane.
• Snell’s law: The ratio of sine of angle of incidence to sine of angle of refraction is constant for a given pair of media. sin i / sin r = n₂₁.
  where n₂₁ = refractive index of 2nd medium w.r.to 1st medium.
• When light rays are travelling from rarer medium to denser medium they will bend towards the normal.
• When light rays are travelling from denser medium to rarer medium they will bend away from normal.

→ Total internal reflection: When light rays are travelling from denser medium to rarer medium for angle of incidence i > i_c light rays are notable to penetrate the boundary layer and come back into the same medium. This phenomena is known as “total internal reflection”.

→ Critical angle (ic): The angle of incidence in the denser medium for which angle of refraction in rarer medium is 90° is called “critical angle” of denser medium.

→ Applications: Due to total internal reflection:

• Formation of mirages on hot summer days on tar roads and in deserts.
• Sparkling of well cut diamonds.
• Prisms designed to bend light rays by 90° or by 180° make use of total internal reflection.
• Optical fibre provides loss less trans-mission overlong distances with total internal reflection.

→ Refraction through lenses:
Lens formula I = \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Lens makers formula \(\frac{1}{f}\) = (n₂₁ – 1) \(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
For any curved spherical surface \(\frac{\mathrm{n}_2}{\mathrm{v}}-\frac{\mathrm{n}_1}{\mathrm{u}}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{R}}\)

→ Power of a lens (P): Power of a lens is defined as the tangent of the angle by which it converges or diverges a beam of light falling at unit distance from the optical centre.
i.e, tan δ = \(\frac{h}{f}\) when δ is small tan δ = δ
δ = \(\frac{h}{f}\) (or) P = \(\frac{1}{f}\)
Power P = j unit: dioptre. Here, f is in meters.

→ Lens combination: When lenses are in contact then their combined focal length
\(\frac{1}{F}=\frac{1}{f_1}+\frac{1}{f_2}+\frac{1}{f_3}\)+…………
Combined power P = P₁ + P₂ + ……………

→ Magnification of combined lens is
m = m₁ × m₂ × m₃ i.e., total magnification is the product of individual magnifications of lenses on that combination.

→ Refraction through prism: In prism path of light ray inside prism is parallel to prism base.
Angle of prism, A = r₁ + r₂.
Angle of deviation δ = i + e – A
where e is angle of emergence.
At minimum deviation position
r₁ = r₂ ⇒ i₁ = r₂
r = \(\frac{A}{2}\) and I = \(\frac{\left(\mathrm{A}+\mathrm{d}_{\mathrm{m}}\right)}{2}\)
Refractive index n₂₁ = \(\frac{\mathrm{n}_2}{\mathrm{n}_1}\)
= \(\frac{\sin \left(\mathrm{A}+\mathrm{d}_{\mathrm{m}}\right) / 2}{\sin \mathrm{A} / 2}\)
For small angled prism dm = (n₂₁ – 1) A.

→ Dispersion: The phenomenon of splitting of light into its constitute colours is known as “dispersion”.
Dispersion takes place due to change in refractive index of medium for different wave lengths.

Note:

• The bending of red component of white light is least due to its longest wavelength.
• Bending of violet component of white light is maximum due to its short wave length.
• In vacuum all colours will travel with same velocity and velocity in vacuum is independent of wavelength of light.

→ Rainbow: Rainbow is due to dispersion of white light through water drops.

→ Scattering: Change in the direction of light rays in an irregular manner is called”scatte-ring”.
Ex: Sun light gets scattered by atmospheric particles.
Note: Light of shorter wavelengths will scatter much more than light of longer wave-length. Due to this, reason blue light will scatter more than red light.

→ Rayleigh scattering: The amount of scattering is inversely proportional to fourth power of the wavelength.
Ex: Blue has shorter wavelength than red. Hence blue will scatter much more strongly. Note: Wavelength of violet is shorter than blue. So violet will scatter more than blue. But our eye is not sensitive to violet. So we will see the blue colour in sky.

→ Human eye: Human eye contains rods and cones. Rods will respond to intensity of light.

→ Accommodation of eye: Our eye consists of a crystalline lens. The curvature and focal length of this lens is controlled by ciliary muscles. When ciliary muscles are relaxed focal length of eye lens is high. So light rays from distant object are focused onto the retina while viewing the near by objects eye lens will become thick and focal length will become less.
The property of eye lens to change its focal length depending on the objects to be viewed is called “accommodation”.

→ Hypermyopia: It is one type of eye defect. Where light rays coming from distant object are converged at a point infront of retina. This defect is called “short sighted-ness or Hypermyopia”. This defect can be compensated by using a concave lens.

→ Hypermetropia: This is one type of eye defect. In this defect eye lens focusses the incoming light at a point behind the retina. This is called “far sightedness or Hyper-metropia”. This defect can be compensated by using a convex lens.

→ Astigmatism: In this type of eye defect cornea will have large curvature in vertical direction and less curvature in horizon¬tal direction. A person with this type of defect can not clearly see objects because carnia has non-uniform radius.
This defect can be reduced by using cylindrical lenses of desired radius of curvature.

→ Simple microscope: A simple convex lens can be used as a simple microscope. Given object is placed between centre of lens and its focus. A virtual image is made to form at near point.
Near point magnification m = (1 + D/f).
If final image is made to form at infinity (far point).
Far point magnification m = D / f.

→ Compound microscope: Magnification of microscope
M = m₀ . m_e = \(\frac{v}{u}\left(1+\frac{D}{f_e}\right)\)
Or
m ≈ \(\frac{L}{f_e} \frac{D}{f_e}\), m₀ = \(\frac{h^{\prime}}{h}=\frac{v}{u}\)

For near point me = (1 + D/f_e)
For far point m = D/f_e.

→ Telescopes: It consists of two convex len¬ses mounted coaxially. Telescope is used to see large objects which are very far away.
Object lens will form a point size real image of object in between the lenses. This first image will act as an object to eye lens. Generally eye lens will form final image at infinity. This is called “Normal adjustment”.

Length of telescope L = f
Manification m = \(\frac{\beta}{\alpha}=\frac{\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\)
Reflecting telescopes are also called “cassegrain telescopes”.
In Telescopes if final image is inverted it is called Astronomical telescope. If final image is erect with respect to object it is called terrestrial telescope.

→ Velocity of light ¡n vacuum c = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
= 3 × 10⁸ m/s
where μ₀ = permeability and E₀= permittivity of vacuum or air (free space).
In a medium the velocity of light (c) = \(\frac{v_1}{v_2}=\frac{v \lambda_1}{v \lambda_2}=\frac{\lambda_1}{\lambda_2}\)
also c = υλ

→ Refractive index of a medium μ = c / V;
where y = velocity of light in medium
From Sneils law μ = sin i / sin r.

→ In refraction or reflection the frequency of light remains constant
₁μ₂ or n₂₁ = \(\frac{v_1}{v_2}=\frac{v \lambda_1}{v \lambda_2}=\frac{\lambda_1}{\lambda_2}\)
Wavelength In medium λ_med = \(\frac{\lambda_{\text {vacuum }}}{\mu(\text { or }) n}\)

→ In refraction n₁λ₁ = n₂λ₂ (In refraction frequency of light υ is constant)

→ Relative refractive index n_r = \(\frac{\mathrm{n}_1}{\mathrm{n}_2}\)
Ex: _wn_g = \(\frac{\mathbf{n}_{\text {glass }}}{\mathbf{n}_{\text {water }}}=\frac{\lambda_{\text {water }}}{\lambda_{\text {glass }}}\)

→ In prism

• r₁ + r₂ = A (angle of prism);
• i₁ + i₂ = A + D (angle of deviation) (or) D = (i₁ – i₂) – A
• n = sin \(\frac{\mathrm{A}+\delta}{2}\)/sin(A/2)where δ = angle of minimum deviation.
• At minimum deviation position i₁ = i₂ and r₁ = r₂.
  So r = A/2 and i = \(\frac{\mathrm{A}+\delta}{2}\)

→ For small angled prisms 6 = (n – 1) A.

→ Relation between critical angle ‘c’ and refractive index n is
n = \(\frac{1}{\sin c}\) or c = sin^-1\(\left[\frac{1}{n}\right]\)

→ Lens makers formula \(\frac{1}{f}\) = (n – 1) \(\left[\frac{1}{n}\right]\)

→ Relation between object distance ‘u’, image distance y and focal length f is = \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)

→ In lens combination \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\) when in contact \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{d}{f_1 f_2}\) when lenses are separated by a distance ‘d.

→ Condition to eliminate spherical aberration by lens combination is separation
d = f₁ – f₂.

→ Conditions to eliminate chromatic aberration:

• In lens combination with separation
  d = \(\frac{\mathrm{f}_1+\mathrm{f}_2}{2}\)
• In achromatic doublet \(\frac{\omega_1}{\mathrm{f}_1}+\frac{\omega_2}{\mathrm{f}_2}\) = 0

→ In simple microscope

• Near point magnification m = \(\left(1+\frac{D}{f}\right)\)
• When image is at Infinity m = \(\frac{D}{f}\)
  where D is the least distance of distinct vision.

→ In compound microscope

• Total magnification m = m₀ × m_e or m = \(\frac{v_0}{u}\left(1+\frac{D}{f_e}\right)\)
• When final Image is at infinity m = \(\frac{L D}{f_0 f_e}\)
• Object lens will form a real image, so m₀ = \(\frac{\mathrm{v}_0}{\mathrm{u}_0}\)
• Eye lens will form a virtual image at near point; so m₀ = (1 + \([latex]\)[/latex])

→ In Telescopes
(a) magnification m = \(\frac{\alpha}{\beta}=\frac{\tan \alpha}{\tan \beta}\) or m = \(\frac{\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\)
At normal adjustment, magnification
m = \(-\frac{\mathrm{f}_0}{\mathrm{f}_e}=\frac{\text { focal length of object lens }}{\text { focal length of eye lens }}\)

(b) When final image is at near point
m = \(-\frac{\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\left(1+\frac{\mathrm{f}_{\mathrm{e}}}{\mathrm{D}}\right)\)

(c) Length of telescope L = f₀ + f_e

(d) In terrestrial telescope length of telescope L = f₀ + f_e + 4f.

→ Dispersive power of prism
w = \(\frac{d_v-d_R}{\frac{d_v+d_g}{2}}=\frac{d_v-d_g}{d}=\frac{\mu_v-\mu_g}{(n-1)}\)
where d_v = Deviation of violet colour;
d_g = Deviation of red colour
\(\frac{\mathrm{d}_{\mathrm{v}}+\mathrm{d}_{\mathrm{g}}}{2}\) = Average deviation

→ Angular dispersive power to = (n_v – n_R)A

→ In prisms the condition for no dispersion is A₁ (n_g – n_R)₁ + A₂ (n_g – n_R)₂ = 0

→ In prisms the condition for no deviation is A₁ (n₁ – 1) + A₂ (n₂ – 1) = 0

→ In lens combination power of combined lens is P = P₁ + P₂ + ……………………

Here students can locate TS Inter 2nd Year Physics Notes 1st Lesson Waves to prepare for their exam.

TS Inter 2nd Year Physics Notes 1st Lesson Waves

→ Wave: A wave is a physical manifestation of disturbance that propagates in space.

→ Transverse waves: In these waves, the con-stituents of the medium will oscillate perpen-dicular to the direction of propagation of the wave.

→ Longitudinal waves: In these waves the constituents of the medium will oscillate paral¬lel to the direction of propagation of the wave.

→ Wave motion can be represented as a func¬tion of both position ‘x’ and time ‘t’.

→ Generally for x – ‘+ve’ direction equation of a wave is y = a sin (kx – ωt – Φ)

→ Crest: It is a point of a maximum positive displacement.

→ Trough: It is a point of maximum negative displacement.

→ Amplitude (a): The maximum displacement of constituents of the medium from means position is called “amplitude” ‘a’.
a = y_max

→ Phase (Φ) Phase gives the displacement of the wave at any position and at any instant.

→ Initial Phase: At initial condition (when x = 0 and t = 0) phase of the wave is called initial phase.

→ Wavelength (λ): The minimum distance between any two successive points of same phase on wave is called “wavelength” A.

→ Propagation constant (OR) angular wave number (k):
\(\frac{2 \pi}{\lambda}\) or A = \(\frac{2 \pi}{\mathrm{k}}\) where ‘A’ is A k

→ Time period (T): Time taken to produce one complete wave (or) time taken to complete one oscillation is known as “Time period T”.

→ Frequency ‘υ’: Number of waves produced per second. (OR) Number of oscillations com¬pleted per second is known as “frequency υ.”
Frequency υ = \(\frac{1}{\mathrm{~T}}\) (Or) Time period T = \(\frac{1}{v}\)

→ Angular frequency (or) velocity (ω):
Angular frequency (w) = 2πυ (or) ω = \(\frac{2 \pi}{\mathrm{T}}\)

→ Relation between velocity v, wavelength A and frequency o is v = υλ (OR) v = λ/T.

→ Speed of a wave in stretched strings:
Speed of transverse wave in stretched wires v =\(\sqrt{\mathrm{T} / \mu}\)
where µ = linear density = mass / length. S.I. unit = kg/metre.

→ Speed of longitudinal waves in different media
In liquids:
v = \(\sqrt{\frac{B}{\rho}}\)
where B = Bulk modulus
ρ = Density.

→ In solids:
v = \(\sqrt{\frac{Y}{\rho}}\)
where Y = Young’s modulus
ρ = Density.

In gases:
According to Newton’s formula
v = \(\sqrt{\frac{P}{\rho}}\)
where P = pressure of the gas and
ρ = density of the gas.
According to Newton – Laplace’s formula
v = \(\sqrt{\frac{\gamma \mathrm{P}}{\rho}}\) where γ = the ratio of specific heats of the gas.

→ Principle of superposition: If two or more waves moving in the medium superposes then the resultant wave form is the sum of wave functions of individual waves.
i.e y = y₁ + y₂ + y₃ + ………

→ Stationary waves (or) standing waves :
When a progressive wave and reflected wave superpose with suitable phase a steady wave pattern is set up on the string or in the medium.
A standing wave is represented by y (x, t) = 2 a sin kx cos ωt.

→ Fundamental mode : The lowest possible natural frequency of a system is called “fundamental mode.”

→ Frequency of fundamental mode is called fundamental frequency (or) first harmonic.

→ Harmonics: Sounds with frequencies equal to integral multiple of a fundamental frequency (n) are called “harmonics.”

→ Resonance : It is a special condition of a system where frequency of external periodic force is equal to or almost equal to natural frequency of a vibrating body.

→ Beats: When two sounds of nearly equal frequencies are produced together they will pro-duce a waxing and waning intensity of sound at observer. This effect is called Heats.”
Beat Frequency Δυ = υ₁ ~ υ₂
Beat Period T = \(\frac{1}{v_1 \sim v_2}\)

→ Doppler’s effect: The apparent change in frequency of sound heard due to relative motion of source and observer is called” Doppler’s effect.”

→ Doppler’s effect is applicable to mechanical waves and also to electromagnetic waves. In sound it is “asymmetric” whereas in light it is “symmetric”.

→ Velocity of sound in a medium v = υλ
where υ = \(\frac{1}{T}\)

→ Propagation constant of wave (k) = \(\frac{2 \pi}{\lambda}\) (Also k is known as angular wave number) Angular velocity of wave (©) = \(\frac{2 \pi}{\lambda}\) = 2πυ; frequency υ = \(\frac{1}{T}=\frac{2 \pi}{\omega}\)

→ Equation of progressive wave in x-positive direction is
y’= a sin (ωt – kx) (or) y = a cos (ωt – kx)
Along – ve direction on X-axis y = a sin (ωt + kx) (or) y = a cos (ωt + kx)

→ From the superposition principle, the dis-placement of the resultant wave is given by y = y₁ + y₂

→ Equation of stationary wave is
y = 2 A sin kx cos ωt or Y = 2A kx sin ωt Here kx and ωt are in separate trigonometric functions.

→ In stretched wires of string
(i) Velocity of transverse vibrations
v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)
where T = tension applied
and ρ = linear density,

(ii) Fundamental frequency of vibration
υ₀ = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)

→ The laws of transverse vibrations in stretched strings

• 1st law, υ ∝ \(\) (OR) \(\frac{v_1}{v_2}=\frac{l_2}{l_1}\)
• 2nd law υ ∝ √T (OR) \(\frac{v_1}{v_2}=\sqrt{\frac{\mathrm{T}_1}{\mathrm{~T}_2}}\)
• 3rd law υ ∝ \(\frac{1}{\sqrt{\mu}}\) (OR) \(\frac{v_1}{v_2}=\sqrt{\frac{\mu_2}{\mu_1}}\)

→ Newton’s equations for velocity of sound in different media.
1. In solids υ_s = \(\sqrt{\frac{Y}{\rho}}\)
Y = Young’s modulus of wire

2. In liquids υ₁ = \(\sqrt{\frac{B}{\rho}}\)
B = Bulk modulus of liquid

3. In gases υ_g = \(\sqrt{\frac{\mathrm{P}}{\rho}}\)
P = Pressure of the gas Laplace corrected the formula for velocity of sound in gases as υ_g = \(\sqrt{\frac{\gamma \mathrm{P}}{\rho}}\)
where γ = \(\frac{C_P}{C_V}\)
γ = Ratio of specific heats of a gas.
Where Y = Young’s modulus of solid,
K = Bulk modulus of the liquid and P is pressure of the gas.

→ In case of closed pipes

• Length of pipe at the fundamental note is l = \(\frac{\lambda}{4}\) ⇒ λ = 4l
• Fundamental frequency of vibration
  υ = \(\frac{\mathrm{v}}{\lambda}=\frac{\mathrm{v}}{4 l}\), υ’ = 3υ, υ” = 5u.
  υ’ and υ” are second harmonic and third harmonics.
• Closes pipes will support only odd har-monics.
  Ratio of frequencies or harmonics is 1: 3: 5: 7 etc.

→ In case of open pipes .
1. Length of pipe at the fundamental note is l,
l = \(\frac{\lambda}{2}\) ⇒ λ = 2l

2. Fundamental frequency of vibration
υ = \(\frac{\mathrm{v}}{\lambda}=\frac{\mathrm{v}}{2 l}\)
υ’ = 2υ, υ” = 3υ.
υ’ and υ” are second and third harmonics.

3. Open pipe will support all harmonics of a fundamental frequency.
Ratio of frequencies = 1: 2: 3: 4

→ Beat frequency Δυ = υ₁ ~ υ₂

→ When a tuning fork is loaded, its frequency of vibration decreases.
Due to loading, beat frequency decreases ⇒ frequency of that fork υ₁, < υ₂ (2nd fork).
When a tuning fork is field then its frequency of vibrating increases.
Due to filing beat frequency increases ⇒ frequency of that fork υ₁ > υ₂ (2nd fork).

→ General equation for Doppler’s effect is
υ’ = \(\left[\frac{v \pm v_0}{v \mp v_s}\right]\)υ
When velocity of medium (v^ is also taken into account apparent frequency
υ’ = \(\left[\frac{v+v_0 \pm v_m}{v \mp v_s \mp v m}\right]\)υ Sign convention is to be applied.
Note: In sign convension direction from observer to source is taken as + ve direction of velocity.

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Complex Numbers Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Complex Numbers Important Questions Very Short Answer Type

Question 1.
Find the additive inverse of (√3, 5). [March ’90]
Solution:
Let z = (√3, 5)
The additive inverse of z is – z = – (√3, 5) = (- √3, – 5)

Question 2.
If z = (cos θ, sin θ), find (z – \(\frac{1}{z}\)). [TS – Mar. 2019]
Solution:
Given that z = (cos θ, sin θ)
The multiplicative inverse of z is
z^-1 = \(\frac{1}{z}=\left(\frac{a}{a^2+b^2}, \frac{-b}{a^2+b^2}\right)\)
= \(\left(\frac{\cos \theta}{\cos ^2 \theta+\sin ^2 \theta}, \frac{-\sin \theta}{\cos ^2 \theta+\sin ^2 \theta}\right)\)
= \(\left(\frac{\cos \theta}{1}, \frac{-\sin \theta}{1}\right)\)
= (cos θ – sin θ)
z – \(\frac{1}{z}\) = (cos θ, sin θ) – (cos θ, – sin θ)
= (cos θ – cos θ, sin θ + sin θ)
= (0, 2 sin θ)

Question 3.
Find the multiplicative inverse of (sin θ, cos θ).
Solution:
Let z = (sin θ, cos θ)
The multiplicative inverse of z is
z^-1 = \(\left(\frac{a}{a^2+b^2}, \frac{-b}{a^2+b^2}\right)\)
z^-1 = \(\left(\frac{\sin \theta}{\cos ^2 \theta+\sin ^2 \theta}, \frac{-\cos \theta}{\cos ^2 \theta+\sin ^2 \theta}\right)\)
= \(\left(\frac{\sin \theta}{1}, \frac{-\cos \theta}{1}\right)\)
= (sin θ, – cos θ)

Question 4.
Express \(\frac{4+2 i}{1-2 i}+\frac{3+4 i}{2+3 i}\) in the form a + ib.
Solution:

Question 5.
Find the real and imaginary parts of the complex number \(\frac{a+i b}{a-i b}\). [TS – Mar. 2015]
Solution:

Question 6.
Express (1 – i)³ (1 + i) in the form a + ib.
Solution:
Let z = (1 – i)³ (1 + i)
= (1 – i)² (1 – i) (1 + i)
= (1 + i² – 2i) (1 – i²)
= (1 – 1 – 2i) (1 – (- 1)) (∵ i² = – 1)
= (- 2i) (2)
= – 4i = 0 + i (- 4)
It is in the form a + ib.

Question 7.
Find the multiplicative inverse of 7 + 24i. [TS – Mar. 2016, AP – May 2015]
Solution:
Let z = 7 + 24i
z^-1 = \(\)
∴ The multiplicative inverse of complex number z = 7 + 24i is
z = \(\left(\frac{7-24 i}{7^2+(24)^2}\right)\)
= \(\left(\frac{7-24 \mathrm{i}}{49+576}\right)=\frac{7-24 \mathrm{i}}{625}\) .

Question 8.
If 4x + i(3x – y) = 3 – 6i where x and y are real numbers, then find the values of\ x and y.
Solution:
Given that 4x + i(3x – y) = 3 – 6i
Comparing real and imaginary parts on both sides
4x = 3
x = \(\frac{3}{4}\)

3x – y = – 6
3 (\(\frac{3}{4}\)) – y = – 6
y = \(\frac{9}{4}\) + 6
= \(\frac{9+24}{4}\)
= \(\frac{33}{4}\)
∴ x = \(\frac{3}{4}\), y = \(\frac{33}{4}\)

Question 9.
Find the complex conjugate of (3 + 4i) (2 – 3i). [May ’14, Mar. 1997, AP – Mar. ’18, May ’16]
Solution:
Let z = (3 + 4i) (2 – 3i)
= 6 – 9i + 8i – 12i²
= 6 – i + 12
z = 18 – i
∴ The conjugate of z is \(\overline{\mathrm{z}}=\overline{(18-\mathrm{i})}\) = 18 + ¡

Question 10.
Find the square root of – 5 + 12i. [Board Paper]
Solution:

Question 11.
Find the square root of – 47 + i. 8√3. [March ’13(old), May ’12, ’09, May ’10, ’03]
Solution:

Question 12.
Simplify i² + i⁴ + i⁶ + …………… + (2n + 1) terms.
Solution:
= i² + i⁴ + i⁶ + …………… + (2n + 1) terms
= i² + (i²)² + (i²)³ + …………….. + (2n + 1) terms
= – 1 + 1 – 1 + ……………. + (2n + 1) terms = – 1

Question 13.
Simplify i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (- i)²⁶.
Solution:
i¹⁸ – 3 . i⁷ + i² (1 + i⁴) (- i)²⁶.
= (i²)⁹ – 3 (i²)³ . i + i² (1 + (i²)²) (i²)¹³
= (- 1)⁹ – 3 (- 1)³ . i + (- 1) (1 + (- 1)²) (- 1)¹³
= – 1 + 3i + 2 = 1 + 3i

Question 14.
If (a + ib)² = x + iy, find x² + y². [TS – May 2015]
Solution:
Given that,
(a + ib)² = x + iy
a² + i²b² + 2abi = x + iy
a² – b² + i(2ab) =x + iy
Comparing real and imaginary parts on both sides
x = a² – b², y = 2ab
∴ x² + y² = (a² + b²)² + 4a²b² = (a² + b²)²

Question 15.
Find the least positive integers n, satisfying \(\left(\frac{1+i}{1-i}\right)^n\) = 1.
Solution:

If n = 4
⇒ i⁴ = 1
∴ The required least positive integer, n = 4.

Question 16.
Write z = – √7 + i √21 in the polar form. [AP – May 2015; March 11]
Solution:

Let, z = – √7 + i √21
= r (cos θ + i sin θ)
then r cos θ = – √7, r sin θ = √21
r = \(\sqrt{x^2+y^2}=\sqrt{(-\sqrt{7})^2+(\sqrt{21})^2}\)
= \(\sqrt{7+21}=\sqrt{28}=2 \sqrt{7}\)
Hence,
2√7 cos θ = – √7
cos θ = \(-\frac{1}{2}\)
2√7 sin θ = √21
2√7 sin θ = √3 . √7
sin θ = \(\frac{\sqrt{3}}{2}\)
∴ θ lies in the Q2.
∴ θ = \(\frac{2 \pi}{3}\)
∴ z = – √7 + i√21
= 2√7 (cos \(\frac{2 \pi}{3}\) + i sin \(\frac{2 \pi}{3}\)).

Question 17.
Express – 1 – i in polar form with principle value of the amplitude.
Solution:

Let, – 1 – i = r (cos θ + i sin θ)
Then r cos θ = – 1; r sin θ = – 1
r = \(\sqrt{(-1)^2+(-1)^2}=\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = – 1
cos θ = \(\frac{-1}{\sqrt{2}}\)
∴ θ lies in the Q3.
∴ θ = – \(\frac{3 \pi}{4}\)

√2 sin θ = – 1
sin θ = \(\frac{-1}{\sqrt{2}}\)

∴ – 1 – i = √2 (cos (- \(\frac{3 \pi}{4}\)) + i sin (- \(\frac{3 \pi}{4}\)))

Question 18.
Express – 1 – i√3 in the modulus amplitude form.
Solution:

Let – 1 – i√3 = r (cos θ + i sin θ)
Then r cos θ = – 1, r sin θ = – √3
r = \(\sqrt{\mathrm{x}^2+\mathrm{y}^2}\)
= \(\sqrt{(-1)^2+(-\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence, 2 cos θ = – 1, 2 sin θ = – √3
cos θ = – \(\frac{1}{2}\), sin θ = \(\frac{-\sqrt{3}}{2}\)
∴ θ lies in the Q3.
∴ θ = – \(\frac{2 \pi}{3}\)
∴ For the given complex number modulus = 2
Principle amplitude = – \(\frac{2 \pi}{3}\)
∴ – 1 – i √3 = 2 [cos (- \(\frac{2 \pi}{3}\)) + i sin (- \(\frac{2 \pi}{3}\))]

Question 19.
If z₁ = – 1 and z₂ = – 1 then find Arg(z₁z₂).
Solution:
Given, z₁ = – 1
= cos π + i sin π
∴ Arg z₁ = π
z₂ = – i
= cos (- \(\frac{\pi}{2}\)) + i sin (- \(\frac{\pi}{2}\))
∴ Arg z₂ = – \(\frac{\pi}{2}\)
Now,
Arg (z₁z₂) = Arg z₁ + Arg z₂
= π – \(\frac{\pi}{2}\) = \(\frac{\pi}{2}\)

Question 20.
If z₁ = – 1, z₂ = i, then find Arg (\(\frac{z_1}{z_2}\)).
[May 14 11, March 09 Board Paper TS-Mar. 16; AP – Mar. 18, 17]
Solution:
Given z₁ = – 1
= cos π + i sin π
∴ Arg z₁ = π
z₂ = i
= cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
∴ Arg z₂ = \(\frac{\pi}{2}\)
Now, Arg \(\left(\frac{\mathrm{z}_1}{\mathrm{z}_2}\right)\) = Arg z₁ – Arg z₂
= π – \(\frac{\pi}{2}\) = \(\frac{\pi}{2}\)

Question 21.
If (cos 2α + i sin 2α) (cos 2β + i sin 2β) = cos θ + i sin θ, then find the value of θ.
Solution:
Given,
(cos 2α + i sin 2α) (cos 2β + i sin 2β) = cos θ + i sin θ
cis (2α) . cis (2β) = cis θ
cis (2α + 2β) = cis θ
cos (2α + 2β) + i sin (2α + 2β) = cos θ + i sin θ
Comparing real parts on both sides, we get
cos θ = (2α + 2β)
θ = 2 (α + β)

Question 22.
If √3 + i = r (cos θ + i sin θ) then find the value of θ in radian measure.
Solution:

Given that,
√3 + i = r (cos θ + i sin θ)
Then r cos θ = √3, r sin θ = 1
r = \(\sqrt{x^2+y^2}=\sqrt{(\sqrt{3})^2+(1)^2}\)
= \(\sqrt{3+1}=\sqrt{4}\) = 2
Hence,
2 cos θ = √3
cos θ = \(\frac{\sqrt{3}}{2}\)
2 sin θ = 1
sin θ = \(\frac{1}{2}\)
∴ θ lies in the Q1.
∴ θ = \(\frac{\pi}{6}\)

Question 23.
If x + iy = cis α . cis β, then find the value of x² + y². [AP – Mar. 18]
Sol.
Given that,
x + iy = cis α . cis β
= cis (α + β)
= cos (α + β) + i sin (α + β)
Now, comparing real parts on both sides.
we get x = cos (α + β)
Comparing imaginary parts on both sides
we get y = sin (α + β)
Now,
x² + y² = cos² (α + β) + sin² (α + β) = 1.

Question 24.
If (√3 + i)¹⁰⁰ = 2⁹⁹ (a + ib) then show that a² + b² = 4. [AP – Mar.2016] [AP – Mar. 2019]
Solution:
Given that,
(√3 + i)¹⁰⁰ = 2⁹⁹ (a + ib)

Squaring on both sides,
a² + b² = 4

Question 25.
If z = x + iy and |z| = 1, then find the locus of z. [TS – Mar. 2019]
Solution:
Given, z = x + iy
|z| = 1
|x + iy| = 1
\(\sqrt{x^2+y^2}\) = 1
Squaring on both sides,
x² + y² = 1
∴ Locus of z is x² + y² = 1.

Question 26.
If the amplitude of (z – 1) is \(\frac{\pi}{2}\) then find the locus of z. [TS – May 2015]
Solution:
Let, z = x + iy
Now, z – 1 = x + iy – 1
= (x – 1) + iy
If z = x + iy then θ = tan^-1 (\(\frac{y}{x}\))
Given that,
the amplitude of (z – 1) is \(\frac{\pi}{2}\)
tan^-1 (\(\frac{y}{x-1}\)) = \(\frac{\pi}{2}\)
\(\frac{y}{x-1}\) = tan \(\frac{\pi}{2}\)
\(\frac{y}{x-1}\) = ∞ = \(\frac{1}{0}\)
x – 1 = 0
x = 1
∴ Locus of z is x = 1.

Question 27.
If the Arg \(\overline{\mathbf{z}}_1\) and Arg z₂ are \(\frac{\pi}{5}\) and \(\frac{\pi}{3}\) respectively, then find (Arg z₁ + Arg z₂). [AP-May, Mar. 2016]
Solution:
If z = x + iy then θ = tan^-1 (\(\frac{y}{x}\))
If \(\overline{\mathrm{Z}}\) = x – iy then θ = tan^-1 (\(\frac{-y}{x}\))
= – tan^-1 (\(\frac{y}{x}\))
Given that,
Arg \(\overline{\mathbf{z}}_1\) = \(\frac{\pi}{5}\)
Arg z₁ = – \(\frac{\pi}{5}\)
Arg z₂ = \(\frac{\pi}{3}\)
Now,
Arg z₁ + Arg z₂ = – \(\frac{\pi}{5}\) + \(\frac{\pi}{3}\)
= \(\frac{-3 \pi+5 \pi}{15}=\frac{2 \pi}{15}\).

Question 28.
If z = \(\frac{1+2 i}{1-(1-i)^2}\) then find Arg(z).
Solution:
z = \(\frac{1+2 i}{1-(1-i)^2}\)
= \(\frac{1+2 \mathrm{i}}{1-\left(1+\mathrm{i}^2-2 \mathrm{i}\right)}\)
= \(\frac{1+2 i}{1-1-i^2+2 i}\)
= \(\frac{1+2 \mathrm{i}}{1+2 \mathrm{i}}\) = 1
∴ z = 1 = 1 + i(0)
∴ Arg z = tan^-1 (\(\frac{y}{x}\))
= tan^-1 (\(\frac{0}{1}\))
= tan (0) = 0°

Question 29.
Simplify \(\frac{(2+4 i)(-1+2 i)}{(-1-i)(3-i)}\) and find its modulus.
Solution:
Given,

Question 30.
Simplify \(\frac{(1+i)^3}{(2+i)(1+2 i)}\) and find its modulus.
Solution:
Given, \(\frac{(1+i)^3}{(2+i)(1+2 i)}\)

Question 31.
If (1 – i) (2 – i) (3 – i) ……….. (1 – ni) = x – iy, then prove that 2 . 5 . 10 …………….. (1 + n²) = x² + y².
Solution:
Given that,
(1 – i) (2 – i) (3 – i) (1 – ni) = x – iy

Squaring on bothsides,
2 . 5 . 10 . …………… (1 + n²) = x² + y².

Question 32.
If the real part of \(\frac{z+1}{z+i}\) is 1, then find the locus of z.
Solution:
Let, z = x + iy
Now,

Given that,
the real part of \(\frac{z+1}{z+i}\) is 1.
⇒ \(\frac{x^2+x+y^2+y}{x^2+(y+1)^2}\) = 0
x² + y² + x + y = x² + y² + 2y + 1
x – y – 1 = 0
∴ The locus of z is x – y – 1 = 0.

Question 33.
If |z – 3 + i| = 4 determine the locus of z. [March 14, May 08]
Solution:
Let z = x + iy
Given, |z – 3 + i| = 4
|x + iy – 3 + i| = 4
|(x – 3) + i (y + 1)| = 4
\(\sqrt{(\mathrm{x}-3)^2+(\mathrm{y}+1)^2}\) = 4
Squaring on both sides
(x – 3)² + (y + 1)² = 16
x² + 9 – 6x + y² + 2y + 1 – 16 = 0
x² + y² – 6x + 2y – 6 = 0
∴ The locus of z is x² + y² – 6x – 2y – 6 = 0.

Question 34.
If |z + ai| = |z – ai|, then find the locus of z.
Solution:
Let, z = x + iy
Given, |z + ai| = |z – ai|
|x + iy + ai| = |x – iy – ai|
|x + i(y + a)| = |x + i(y – a)|
\(\sqrt{(x)^2+(y+a)^2}=\sqrt{(x)^2+(y-a)^2}\)
Squaring on both sides
x² + (y + a)² = x² + (y – a)²
(y + a)² – (y – a)² = 0
4ya = 0
y = 0
∴ The locus of z is y = 0.

Question 35.
Find the equation of the straight line joining the points represented by (- 4 + 3i), (2 – 3i) in the Argand plane.
Solution:
Let the two complex numbers be represented in the Argand plane by the points P, Q respectively.
Then P = (- 4, 3), Q = (2, – 3)
∴ The equation of \(\overline{\mathrm{PQ}}\) is
y – y₁ = \(\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathrm{x}_2-\mathrm{x}_1}\) (x – x₁)
y – 3 = \(\frac{-3-3}{2+4}\) (x + 4)
y – 3 = \(\frac{-6}{6}\) (x + 4)
y – 3 = – 1 (x + 4)
y – 3 = – x – 4
x + y + 1 = 0.

Question 36.
z = x + iy represents a point in the Argand plane. Find the locus of z such that z = 2.
Solution:
Given, z = x + iy
=> P = (x, y)
|z| = 2
|x + iy| = 2
\(\sqrt{\mathrm{x}^2+\mathrm{y}^2}\) = 2
Squaring on both sides
x² + y² = 4
x² + y² – 4 = 0
∴ Locus of P is x² + y² – 4 = 0
The locus represents a circle with centre (0, 0) and radius 2 units.

Question 37.
The point ‘P’ represents a complex number z in the Argand plane. If the amplitude of z is \(\frac{\pi}{4}\), determine the locus of P.
Solution:
Let z = x + iy
⇒ P = (x, y)
Given that,
Amp(z) = \(\frac{\pi}{4}\)
tan^-1 (\(\frac{y}{x}\)) = \(\frac{\pi}{4}\)
\(\frac{y}{x}\) = tan \(\frac{\pi}{4}\)
\(\frac{y}{x}\) = 1
y = x
x = y
∴ Locus of P is x = y i.e., x – y = 0.
The locus represents a line passing through origin and making an angle of 45° with the (+) ve direction of X – axis.

Question 38.
Find the equation of the perpendicular bisector of the line segment joining the points 7 + 7i, 7 – 7i in the Argand plane.
Solution:

Let the two complex numbers be represented in the Argand plane by the points P, Q respectively.
Then P = (7, 7), Q = (7, – 7)
Since, C is the midpoint of \(\overline{\mathrm{PQ}}\) then
C = \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2}{2}, \frac{\mathrm{y}_1+\mathrm{y}_2}{2}\right)\)
= \(\left(\frac{7+7}{2}, \frac{7-7}{2}\right)=\left(\frac{14}{2}, \frac{0}{2}\right)\) = (7, 0)
Slope of \(\overline{\mathrm{PQ}}\) is m = \(\frac{y_2-y_1}{x_2-x_1}\)
= \(\frac{-7-7}{7-7}=\frac{-14}{0}\)
∵ \(\overline{\mathrm{AB}}\) is ⊥ to \(\overline{\mathrm{PQ}}\) then
slope of \(\overline{\mathrm{AB}}\) = \(\frac{-1}{\mathrm{~m}}=\frac{-1}{\frac{-14}{0}}\) = o
The equation of the straight line \(\overline{\mathrm{AB}}\) is
y – y₁ = \(-\frac{1}{m}\) (x – x₁)
y – 0 = 0 (x – 7)
⇒ y = 0.

Question 39.
Find the equation of the straight line joining the points – 9 + 6i, 11 – 4i in the Argand plane.
Solution:
Let the two complex numbers be represented in the Argand plane by the point P, Q respectively.
Then P = (- 9, 6), Q = (11, – 4)
∴ The equation of \(\overline{\mathrm{PQ}}\) is
y – y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x – x₁)
y – 6 = \(\frac{-4-6}{11+9}\) (x + 9)
y-6 = \(\frac{-10}{20}\) (x + 9)
y – 6 = \(\frac{-1}{2}\) (x + 9)
2y – 12 = – x – 9
x + 2y – 3 = 0.

Question 40.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i – 2 – 2i, – 2√3 + 2√3i are the vertices of an equilateral triangle. [AP – May 15, 07, TS-Mar. 18]
Solution:
Let the three complex numbers be represented in the Argand plane by the points P, Q, R respectively.
Then P = (2, 2), Q = (- 2, – 2). R = (- 2√3, 2√3)
Now,
PQ = \(\sqrt{(2+2)^2+(2+2)^2}\)
= \(\sqrt{(4)^2+(4)^2}=\sqrt{16+16}=\sqrt{32}\)

QR = \(\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2}\)
= \(\sqrt{4+12-8 \sqrt{3}+4+12+8 \sqrt{3}}=\sqrt{32}\)

PR = \(\sqrt{(2+2 \sqrt{3})^2+(2-2 \sqrt{3})^2}\)
= \(\sqrt{4+12+8 \sqrt{3}+4+12-8 \sqrt{3}}=\sqrt{32}\)

∴ PQ = QR = PR
∴ Given points form an equilateral triangle.

Question 41.
If z = 2 – 3i, then show that z² – 4z + 13 = 0. [TS- Mar. 18, Mar. 08, AP – Mar. 2019]
Solution:
Given that z = 2 – 3i
z – 2 = – 3i
Squaring on both sides
(z – 2)² = (- 3i)²
z² + 4 – 4z = 9i²
z² – 4z + 4 = – 9
∴ z² – 4z + 13 = 0

Question 42.
Find the multiplicative inverse of (3, 4).
Solution:
(\(\frac{3}{25}\), \(\frac{4}{25}\))

Question 43.
Write \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\) in the form of a + ib.
Solution:
\(\frac{-8}{13}\) + i (0)

Question 44.
Write the complex number (1 + 2i)³ in the form a + ib. [TS – Mar. 2017]
Solution:
– 11 – 2i

Question 45.
Find the multiplicative inverse of √5 + 3i.
Solution:
\(\frac{\sqrt{5}}{14}-\frac{3}{14} i\)

Question 46.
Write the conjugate of (2 + 5i) (- 4 + 6i).
Solution:
– 38 + 8i.

Question 47.
Find the square roots of 3 + 4i. [March ’13 (old). May ’12, ’09, May ’10, ’03]
Solution:
± (2 + i)

Question 48.
Find the square roots of 7 + 24i. [TS – May 2016, Mar. ‘14]
Solution:
± (4 + 3i)

Question 49.
Find the square roots of – 8 – 6i.
Solution:
± (1 – 3i)