Here students can locate TS Inter 2nd Year Physics Notes 2nd Lesson Ray Optics and Optical Instruments to prepare for their exam.
TS Inter 2nd Year Physics Notes 2nd Lesson Ray Optics and Optical Instruments
→ In ray optics, light will travel from one point to another point along a straight line. The path is called a “ray of light”. A bundle of such rays is called “a beam of light”.
→ Laws of reflection:
- Angle of reflection is equals to angle of incidence (r = i).
- The incident ray, the reflected ray and normal to the reflecting surface lie in the same plane.
→ Spherical mirrors:
- Pole (P): The geometrical centre of spherical mirror is called ‘pole ‘P’.”
- Principal axis: The line joining the pole (P) and centre of curvature ‘C’ of a spherical mirror is known as “principal axis”. Principal focus: For mirrors, after reflection a parallel beam of light w.r.to principal axis will converge or appears to diverge from a point on principal axis. This point is called “principal focus” ‘F’.
- Focal length (f): Distance between principal focus and pole of mirror or centre of lens is called “focal length”.
In spherical mirrors:
- Focal length of concave mirror is positive.
- Focal length of convex mirror is ve1.
- Relation between radius of curvature of mirror R and focal length f is R = 2f
→ Cartesian sign convention:
- All distances must be measured from the pole of the mirror or the optical centre of lens.
- The distances measured along the direction of the incident ray are taken as positive and the distances measured against the direction of incident ray are taken as negative.
- Distances measured above the principal axis of mirror (or) lens are taken as positive. The distances measured below are taken as ve’.
→ Mirror equation = \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
→ Linear Magnification (m): The ratio of height of image (ht) to height of object (hj is called “linear magnification”. Linear magnification (m) = \(\frac{\mathbf{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}}=\frac{-\mathrm{v}}{\mathbf{u}}\)
![]()
→ Refraction: The bending nature of light rays at refracting surface while travelling from one medium to another medium.
→ Laws of refraction:
- The incident ray, the refracted ray and normal to the interface at the point of incidence all lie in the same plane.
- Snell’s law: The ratio of sine of angle of incidence to sine of angle of refraction is constant for a given pair of media. sin i / sin r = n21.
where n21 = refractive index of 2nd medium w.r.to 1st medium. - When light rays are travelling from rarer medium to denser medium they will bend towards the normal.
- When light rays are travelling from denser medium to rarer medium they will bend away from normal.
→ Total internal reflection: When light rays are travelling from denser medium to rarer medium for angle of incidence i > ic light rays are notable to penetrate the boundary layer and come back into the same medium. This phenomena is known as “total internal reflection”.
→ Critical angle (ic): The angle of incidence in the denser medium for which angle of refraction in rarer medium is 90° is called “critical angle” of denser medium.
→ Applications: Due to total internal reflection:
- Formation of mirages on hot summer days on tar roads and in deserts.
- Sparkling of well cut diamonds.
- Prisms designed to bend light rays by 90° or by 180° make use of total internal reflection.
- Optical fibre provides loss less trans-mission overlong distances with total internal reflection.
→ Refraction through lenses:
Lens formula I = \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
Lens makers formula \(\frac{1}{f}\) = (n21 – 1) \(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
For any curved spherical surface \(\frac{\mathrm{n}_2}{\mathrm{v}}-\frac{\mathrm{n}_1}{\mathrm{u}}=\frac{\mathrm{n}_2-\mathrm{n}_1}{\mathrm{R}}\)
→ Power of a lens (P): Power of a lens is defined as the tangent of the angle by which it converges or diverges a beam of light falling at unit distance from the optical centre.
i.e, tan δ = \(\frac{h}{f}\) when δ is small tan δ = δ
δ = \(\frac{h}{f}\) (or) P = \(\frac{1}{f}\)
Power P = j unit: dioptre. Here, f is in meters.
→ Lens combination: When lenses are in contact then their combined focal length
\(\frac{1}{F}=\frac{1}{f_1}+\frac{1}{f_2}+\frac{1}{f_3}\)+…………
Combined power P = P1 + P2 + ……………
→ Magnification of combined lens is
m = m1 × m2 × m3 i.e., total magnification is the product of individual magnifications of lenses on that combination.
→ Refraction through prism: In prism path of light ray inside prism is parallel to prism base.
Angle of prism, A = r1 + r2.
Angle of deviation δ = i + e – A
where e is angle of emergence.
At minimum deviation position
r1 = r2 ⇒ i1 = r2
r = \(\frac{A}{2}\) and I = \(\frac{\left(\mathrm{A}+\mathrm{d}_{\mathrm{m}}\right)}{2}\)
Refractive index n21 = \(\frac{\mathrm{n}_2}{\mathrm{n}_1}\)
= \(\frac{\sin \left(\mathrm{A}+\mathrm{d}_{\mathrm{m}}\right) / 2}{\sin \mathrm{A} / 2}\)
For small angled prism dm = (n21 – 1) A.
→ Dispersion: The phenomenon of splitting of light into its constitute colours is known as “dispersion”.
Dispersion takes place due to change in refractive index of medium for different wave lengths.
Note:
- The bending of red component of white light is least due to its longest wavelength.
- Bending of violet component of white light is maximum due to its short wave length.
- In vacuum all colours will travel with same velocity and velocity in vacuum is independent of wavelength of light.
→ Rainbow: Rainbow is due to dispersion of white light through water drops.
![]()
→ Scattering: Change in the direction of light rays in an irregular manner is called”scatte-ring”.
Ex: Sun light gets scattered by atmospheric particles.
Note: Light of shorter wavelengths will scatter much more than light of longer wave-length. Due to this, reason blue light will scatter more than red light.
→ Rayleigh scattering: The amount of scattering is inversely proportional to fourth power of the wavelength.
Ex: Blue has shorter wavelength than red. Hence blue will scatter much more strongly. Note: Wavelength of violet is shorter than blue. So violet will scatter more than blue. But our eye is not sensitive to violet. So we will see the blue colour in sky.
→ Human eye: Human eye contains rods and cones. Rods will respond to intensity of light.
→ Accommodation of eye: Our eye consists of a crystalline lens. The curvature and focal length of this lens is controlled by ciliary muscles. When ciliary muscles are relaxed focal length of eye lens is high. So light rays from distant object are focused onto the retina while viewing the near by objects eye lens will become thick and focal length will become less.
The property of eye lens to change its focal length depending on the objects to be viewed is called “accommodation”.
→ Hypermyopia: It is one type of eye defect. Where light rays coming from distant object are converged at a point infront of retina. This defect is called “short sighted-ness or Hypermyopia”. This defect can be compensated by using a concave lens.
→ Hypermetropia: This is one type of eye defect. In this defect eye lens focusses the incoming light at a point behind the retina. This is called “far sightedness or Hyper-metropia”. This defect can be compensated by using a convex lens.
→ Astigmatism: In this type of eye defect cornea will have large curvature in vertical direction and less curvature in horizon¬tal direction. A person with this type of defect can not clearly see objects because carnia has non-uniform radius.
This defect can be reduced by using cylindrical lenses of desired radius of curvature.
→ Simple microscope: A simple convex lens can be used as a simple microscope. Given object is placed between centre of lens and its focus. A virtual image is made to form at near point.
Near point magnification m = (1 + D/f).
If final image is made to form at infinity (far point).
Far point magnification m = D / f.
→ Compound microscope: Magnification of microscope
M = m0 . me = \(\frac{v}{u}\left(1+\frac{D}{f_e}\right)\)
Or
m ≈ \(\frac{L}{f_e} \frac{D}{f_e}\), m0 = \(\frac{h^{\prime}}{h}=\frac{v}{u}\)
For near point me = (1 + D/fe)
For far point m = D/fe.
→ Telescopes: It consists of two convex len¬ses mounted coaxially. Telescope is used to see large objects which are very far away.
Object lens will form a point size real image of object in between the lenses. This first image will act as an object to eye lens. Generally eye lens will form final image at infinity. This is called “Normal adjustment”.
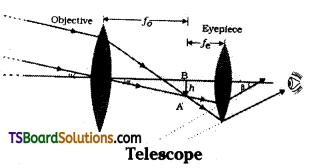
Length of telescope L = f
Manification m = \(\frac{\beta}{\alpha}=\frac{\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\)
Reflecting telescopes are also called “cassegrain telescopes”.
In Telescopes if final image is inverted it is called Astronomical telescope. If final image is erect with respect to object it is called terrestrial telescope.
![]()
→ Velocity of light ¡n vacuum c = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
= 3 × 108 m/s
where μ0 = permeability and E0= permittivity of vacuum or air (free space).
In a medium the velocity of light (c) = \(\frac{v_1}{v_2}=\frac{v \lambda_1}{v \lambda_2}=\frac{\lambda_1}{\lambda_2}\)
also c = υλ
→ Refractive index of a medium μ = c / V;
where y = velocity of light in medium
From Sneils law μ = sin i / sin r.
→ In refraction or reflection the frequency of light remains constant
1μ2 or n21 = \(\frac{v_1}{v_2}=\frac{v \lambda_1}{v \lambda_2}=\frac{\lambda_1}{\lambda_2}\)
Wavelength In medium λmed = \(\frac{\lambda_{\text {vacuum }}}{\mu(\text { or }) n}\)
→ In refraction n1λ1 = n2λ2 (In refraction frequency of light υ is constant)
→ Relative refractive index nr = \(\frac{\mathrm{n}_1}{\mathrm{n}_2}\)
Ex: wng = \(\frac{\mathbf{n}_{\text {glass }}}{\mathbf{n}_{\text {water }}}=\frac{\lambda_{\text {water }}}{\lambda_{\text {glass }}}\)
→ In prism
- r1 + r2 = A (angle of prism);
- i1 + i2 = A + D (angle of deviation) (or) D = (i1 – i2) – A
- n = sin \(\frac{\mathrm{A}+\delta}{2}\)/sin(A/2)where δ = angle of minimum deviation.
- At minimum deviation position i1 = i2 and r1 = r2.
So r = A/2 and i = \(\frac{\mathrm{A}+\delta}{2}\)
→ For small angled prisms 6 = (n – 1) A.
→ Relation between critical angle ‘c’ and refractive index n is
n = \(\frac{1}{\sin c}\) or c = sin-1\(\left[\frac{1}{n}\right]\)
→ Lens makers formula \(\frac{1}{f}\) = (n – 1) \(\left[\frac{1}{n}\right]\)
→ Relation between object distance ‘u’, image distance y and focal length f is = \(\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\)
→ In lens combination \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\) when in contact \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{d}{f_1 f_2}\) when lenses are separated by a distance ‘d.
→ Condition to eliminate spherical aberration by lens combination is separation
d = f1 – f2.
→ Conditions to eliminate chromatic aberration:
- In lens combination with separation
d = \(\frac{\mathrm{f}_1+\mathrm{f}_2}{2}\) - In achromatic doublet \(\frac{\omega_1}{\mathrm{f}_1}+\frac{\omega_2}{\mathrm{f}_2}\) = 0
→ In simple microscope
- Near point magnification m = \(\left(1+\frac{D}{f}\right)\)
- When image is at Infinity m = \(\frac{D}{f}\)
where D is the least distance of distinct vision.
→ In compound microscope
- Total magnification m = m0 × me or m = \(\frac{v_0}{u}\left(1+\frac{D}{f_e}\right)\)
- When final Image is at infinity m = \(\frac{L D}{f_0 f_e}\)
- Object lens will form a real image, so m0 = \(\frac{\mathrm{v}_0}{\mathrm{u}_0}\)
- Eye lens will form a virtual image at near point; so m0 = (1 + \([latex]\)[/latex])
![]()
→ In Telescopes
(a) magnification m = \(\frac{\alpha}{\beta}=\frac{\tan \alpha}{\tan \beta}\) or m = \(\frac{\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\)
At normal adjustment, magnification
m = \(-\frac{\mathrm{f}_0}{\mathrm{f}_e}=\frac{\text { focal length of object lens }}{\text { focal length of eye lens }}\)
(b) When final image is at near point
m = \(-\frac{\mathrm{f}_0}{\mathrm{f}_{\mathrm{e}}}\left(1+\frac{\mathrm{f}_{\mathrm{e}}}{\mathrm{D}}\right)\)
(c) Length of telescope L = f0 + fe
(d) In terrestrial telescope length of telescope L = f0 + fe + 4f.
→ Dispersive power of prism
w = \(\frac{d_v-d_R}{\frac{d_v+d_g}{2}}=\frac{d_v-d_g}{d}=\frac{\mu_v-\mu_g}{(n-1)}\)
where dv = Deviation of violet colour;
dg = Deviation of red colour
\(\frac{\mathrm{d}_{\mathrm{v}}+\mathrm{d}_{\mathrm{g}}}{2}\) = Average deviation
→ Angular dispersive power to = (nv – nR)A
→ In prisms the condition for no dispersion is A1 (ng – nR)1 + A2 (ng – nR)2 = 0
→ In prisms the condition for no deviation is A1 (n1 – 1) + A2 (n2 – 1) = 0
→ In lens combination power of combined lens is P = P1 + P2 + ……………………