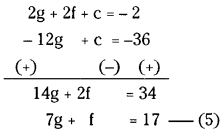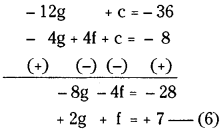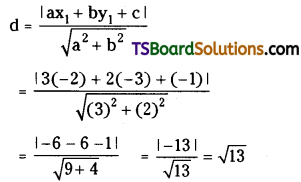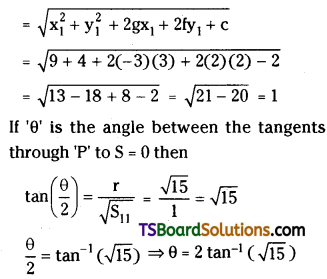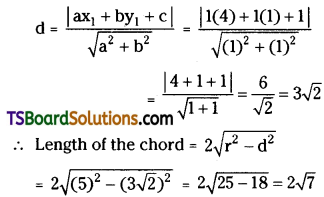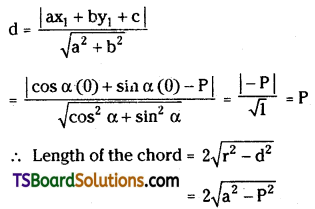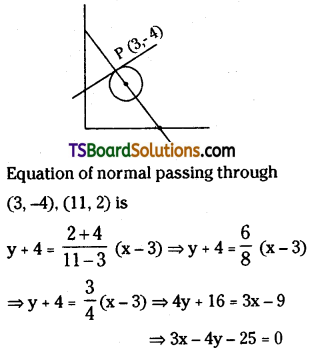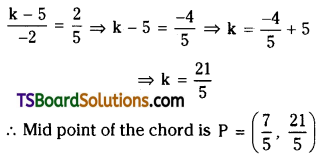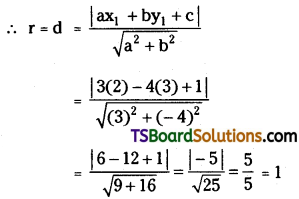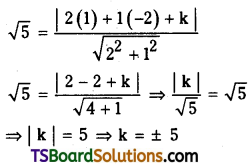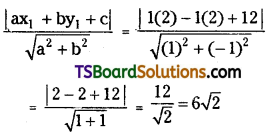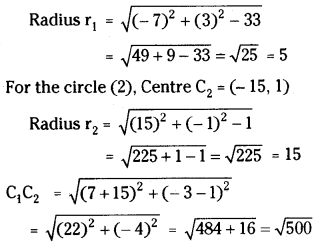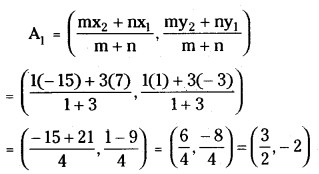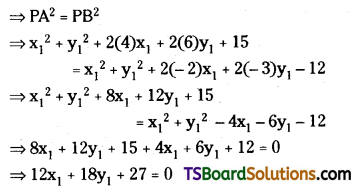Mahesh

Here students can locate TS Inter 2nd Year Physics Notes 9th Lesson Electromagnetic Induction to prepare for their exam.

TS Inter 2nd Year Physics Notes 9th Lesson Electromagnetic Induction

→ Faraday and Henry experiments & con-clusions.

• It is the relative motion between the magnet and the coil that is responsible for genera¬tion of electric current in a coil.
• The motion of a coil towards a stationary magnet or motion of a magnet towards a stationary coil will produce the same effect.
• The direction of current produced when magnet is taken away from coil or coil is taken away from magnet is opposite to that of current produced when magnet is appro-aching the coil or coil is approaching the magnet.
• If a steady current is passed through one coil and another coil is brought nearer to it then it is the relative motion between the coils that induces the electric current.

→ Magnetic flux: The number of magnetic field lines crossing unit area when placed normal to the field at that point is defined as “magnetic flux”.
Magnetic flux, Φ = B̅. A̅ = B A cos 0
Note: The concept of magnetic flux in magnetism is similar to volume flux of a liquid in Hydrostatics.

→ Faraday’s law of Induction:
The time rate of change of magnetic flux through a circuit induces emf in it.
Induced emf, ε = –\(\frac{d \phi_{\mathrm{B}}}{\mathrm{dt}}\)
If there are ‘N’ turns in the coil then = -N \(\frac{d \phi_{\mathrm{B}}}{\mathrm{dt}}\)

→ Lenz’s law: The polarity of induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produces current in that coil.

Note:

• When North pole is brought near to a coil North pole is induced in the coil facing North pole.
• When South pole is brought near to a coil South pole is induced in the coil facing that South pole.

→ Motional emf: When a straight conductor is moving through a uniform and time independent magnetic field then emf is induced across that conductor.
Induced emf, ε = B/v

→ Energy consideration of motion of a conductor in a magnetic field: When a conductor of resistance Vand length T is moving in a magnetic field B then
Induced emf, ε = B/v; current I = \(\frac{\mathrm{B} l \mathrm{v}}{\mathrm{r}}\)
Force on a charged condutor F = I/B = \(\frac{\mathrm{B}^2 l^2 \mathrm{v}}{\mathrm{r}}\)
Power associated with motioi jf wire P = F × v = B²I²v² /r

→ Eddy currents: When large pieces of con-ductors are subjected to changing magne-tic flux then current is induced in them. These induced currents are called “Eddy currents”.
Eddy currents will oppose the motion of the coil or they oppose the change in magnetic flux.
Eddy currents can be minimised by using laminations of metal to make a metal core with a dielectric seperation between them. Ex: Core of transformer.

→ Some applications of eddy currents are

• Magnetic breaking of trains
• Electro-magnetic damping of oscillations
• Induction furnace and
• Electric power motors.

→ Inductance:
The process of producing emf in a coil due to changing current in that coil or in a coil near by it is called Inductance.
Flux associated with a coil Φ_B is proportional to current i.e., Φ_B ∝ I
Rate of change in flux \(\frac{d \phi_B}{d t} \propto \frac{d I}{d t}\) or \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = constant.\(\frac{\mathrm{dl}}{\mathrm{dt}}\)
This constant of proportionality is called Inductance.

Note:

• Inductances are of two types
  • Self inductance (L),
  • Mutual inductance (M)
• Inductance is a scalar quantity; S.I. unit: Henry; Dimensions ML² T^-2 A^-2

→ Self inductance (L): If emf is induced in a single isolated coil due to change of flux in that coil by means of changing current through that coil then that phenomenon is called “Self inductance L”.
In Self inductance, ε = -L\(-\frac{\mathrm{dI}}{\mathrm{dt}}\)
Its SI unit is henry (H)
Note: The rate of self inductance in electromagnetism is similar to inertia in mechanics.

→ Mutual inductance (M): The phenomenon of inducing emf in one coil due to changing magnetic flux in other coil is called “Mutual inductance (M)”.
Mutual Induced emf, ε = -M\(\left(\frac{\mathrm{di}}{\mathrm{dt}}\right)\)

→ AC Generators: In AC generators induced emf or current in loop changes with the orientation of loop between two magnetic poles.
i.e., In AC generator a coil of area (A) is rotated in a stationary magnetic field (B) with some mechanical arrangement.
Flux linked Φ = BA cos θ per loop, or Φ = NBA cos θ for a coil of N turns, where θ = ωt
Induced emf, ε = -N\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = -NBA\(\frac{\mathrm{d}}{\mathrm{dt}}\)(cos θ)
or ε = – NBA ωsin ωt OR ε = – NBA to sin ωt
The term NBAω is also called ε_max

Types of AC generators:

• Hydro-electric generators: In an AC generator if the coil is rotated in magnetic field with the mechanical power pro¬duced by water then it is called Hydroelectric generator.
• Thermal generators: In this type of AC generators energy necessary to rotate the coil in magnetic field is obtained by heating water with coal or some other sources like gas or furnace oil.
• Nuclear generators: In this type of AC generators energy necessary to rotate the coil in magnetic field is obtained by heating water with nuclear fuel.

→ Magnetic flux, Φ = B̅ .A̅ = B A cos θ
Where ‘θ’ is the angle between B̅ and A̅.

→ Induced emf ε = \(\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) for a loop of one turn
(OR) ε = -N\(\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) for a coil of N turns

→ Motional emf of a conductor in magnetic field ε = \(\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = -Bl\(\frac{\mathrm{dx}}{\mathrm{dt}}\) = -B/V dt
ε = Blv

→ Current in the wire, I = \(\frac{\varepsilon}{\mathrm{r}}=\frac{-\mathrm{B} l \mathrm{v}}{\mathrm{r}}\), where ‘r’ is the resistance of wire

→ Force on the conductor, F = IlB = \(\frac{\mathrm{B}^2 l^2 \mathrm{v}}{\mathrm{r}}\)

→ Power associated with the motion P = Fv = IlBV = B²I²V²/r

→ Mutual Inductance M = μ₀n₁n₂πr₁²l
Energy stored in a coil W = \(\frac{1}{2}\)Li²

→ AC Generators:

• Angular displacement of coil θ = ωt ω = Angular velocity of coil
• Flux linkage with coil Φ_B = B̅ .A̅ = B A cos θ = BA cos ωt
• Induced emf, ε = -N\(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = NBAω sin ωt
• Maximum emf induced, ε_m = NBAω
• emf. at any time, ε = ε_max sinωt = ε_maxsin(2πυt)
  where υ is frequency of rotation.

Here students can locate TS Inter 2nd Year Physics Notes 12th Lesson Dual Nature of Radiation and Matter to prepare for their exam.

TS Inter 2nd Year Physics Notes 12th Lesson Dual Nature of Radiation and Matter

→ Cathode rays: Cathode rays are produced in a discharge tube at a pressure of 0.001 mm and at a potential of 10,000V.

• Cathode rays consists of a steam of fast moving negatively charged particles.
• Speed of cathode rays ranges about 0.1 to 0.2 times light velocity (3 × 10⁸m/s)
• From Millikan’s oil drop experiment charge on electron was found to be 1.602 × 10^-19C.

→ Electron emission: A free electron is held inside a metal surface due to attractive forces of ions.
An electron can come out of the metal surface only if it has got sufficient energy to overcome the attractive force.

→ Work function (Φ) : The minimum energy required by an electron to escape from metal surface is called “work function”.
Work function depends on nature of metal.

Note:
In metals, work function of platinum is highest Φ_p = 5.65 eV,
Work function of caesium is lowest Φ_p = 2.14.

→ Electron volt (eV): One electron volt is the energy acquired by an electron when it is accelerated through a potential of 1 volt.
1 eV= 1.602 × 10¹⁹ joules

→ Thermionic emission: In thermionic emission electrons (metal surfaces) are heated to gain sufficient thermal energy to leave the metal surface.

→ Field emission: In field emission strong electric field is applied on metal so that electrons can be pulled out of the metal.

→ Photo-electric emission: When metal surfaces are illuminated with light waves of suitable energy electrons are emitted from metal surface. This process is called”photo electric emission”.

→ Photo electric effect: The process of libe-rating an electron from the metal surface due to light energy falling on it is called “photo electric effect”.

→ Hallwach’s and Lenard’s observations:
I. Lenard allowed ultraviolet light to fall on metal electrodes placed in an evacuated glass tube. He observed that current is flow¬ing in the circuit. When ultraviolet radiations were stopped immediately current flow was also stopped.

II. Hallwach’s conducted experiments on zinc plates exposed to ultraviolet radiation.

• When a negatively charged zinc plate is exposed to U.V. radiation it lost negative charge.
• When a positively charged zinc plate is exposed to U.V. radiation its positive charge increased.
  From above observations he concluded that
  • Negatively charged particles are emitted from zinc plate under the action of U.V. rays.
  •  When frequency of incident light is lesser than a certian value called thres¬hold frequency electrons are not liberated from zinc surface.

→ Stopping potential: The minimum negative potential required by collector to stop photo current (or) becomes zero is called “cut off voltage (v₀)”
K_max = ev₀ (or) \(\frac{1}{2}\)mV_max = ev₀

→ Effect of frequency on stopping potential:

• Stopping potential varies linearly with frequency of incident light.
• Every photo surface has a minimum cut off frequency for which stopping potential V₀ = 0

→ Laws of photo electric emission

• Photo electric emission is an instanta¬neous process where time delay is 10^-9 seconds or even less
• Every photo surface has a minimum cut of frequency v₀ called threshold frequency. Photo emission takes place when frequency of incident radiation υ > υ₀
• For frequency υ > υ₀ photo current is directly proportional to intensity of incident light.
• When frequency of incident light υ > υ₀ kinetic energy of photo electron is directly proportional to frequency υ.
  i. e., KE ∝ υ (i.e., υ > υ₀)

→ Photo electric effect: Wave theory of light As per wave theory photo electric emission must follow the following rules.

• When intensity of light is high energy absorbed by electrons is also high so liberation of electron and its kinetic energy must depend on intensity of light.
• Threshold frequency limit should not exist.
• Energy absorption by electrons from incident light waves is a slow process. Explicit calculations estimated that it may take hours together to liberate electrons from given metal surface. Practically photo electric effect is not at all obeying any prediction from wave theory of light.

→ Einstein’s photo electric equation: According to Einstein radiation consists of discrete units of energy called quanta of energy radiation.
Energy of quanta called photon in light E = hυ
Maximum kinetic energy of photo electron K_max is the difference of energy of incident radiation (hυ) and its work function (t)>).
K_max = hυ – Φ (when υ > υ₀)
or \(\frac{1}{2}\)V_max = h(υ – υ₀)
Work function Φ₀ = hυ₀

→ Millikan’s verification of photo electric equation : Millikan practically verified Einstein’s photo electric equation and found slope of v₀ – υ graph is \(\frac{h}{e}\). He calculated h value from \(\frac{h}{e}\) value obtained from υ₀ – υ graph. It coincides with h’ value obtained by other scientists.

→ Particle nature of light: In photo electric effect energy of quanta interacted with electrons. Energy of quanta E = hυ, momentum p = \(\frac{\mathrm{hv}}{\mathrm{c}}\)
Since energy quanta has momentum p and a fixed value of energy it is treated as particle. Energy quanta of light is called photon.

→ Properties of photons:

• Energy of photon E = hυ, momentum p = \(\frac{\mathrm{hv}}{\mathrm{c}}\)
• In interaction of radiation with matter light quanta will behave like particles.
• Photons are electrically neutral. So they are not deflected by electric and magnetic fields.
• In photon – particle collision total energy and total mometum are conserved. On collision photon will totally loose its enery and momentum.
  Note : In collision between photon and particles total number of photons may not be conserved.

→ Dual nature of light : Light shows wave nature in physical phenomena like interference, diffraction and polarisation.
Light shows particle nature in explaining the phenomena like photo electric effect and compton effect.
So we will consider either wave nature or particle nature depending on the experiment.
Ex:- In case of human eye light gathering by eye lens is explained with wave nature. Where as absorption of energy by rods and cones in retina are explained by particle nature of light.

→ de – Broglie hypothesis: Radiation has dual nature i.e., energy can exist as a wave or as a particle. He assumed that like energy matter will also have dual nature, i.e., matter will have energy and wave nature.
Wave length associated with moving particle λ = \(\frac{h}{p}=\frac{h}{m v}\) = is called de – Broglie wave length.
Experimental results proved wave nature of matter.

→ Heisenberg’s uncertainty principle: According to Heisenberg’s uncertainty principle we cannot exactly find both momentum and position of an electron at the same time.

→ Davisson and Germer experiment: It verified de-Broglie hypothesis.

→ Photo cell: A photo cell will convert light energy into electrical energy. In these cells intensity variation of light is converted into charges in electrical current. They are widely used in recording and reproduction of sound, automatic switches and in automatic counters.

→ Energy of photon E = hυ ⇒ E = \(\frac{\mathrm{hc}}{\lambda}\)
Maximum kinetic energy of photo electron K_max = eV₀

→ Work function Φ₀ = hυ₀ ‘ υ₀ = \(\frac{\phi_0}{\mathrm{~h}}\)
Einsteins’s photo electric equation
K_max = hυ – Φ₀ or eV₀ = hυ – Φ₀
Where V₀ = Stopping potential.

→ de – BrogUe wave length, λ = \(\frac{h}{p}=\frac{h}{m v}\) or \(\frac{h}{p}=\frac{c}{v}\) = λ

→ Kinetic energy of electron in electric field K = eV
Wavelength, λ = \(\frac{h}{p}=\frac{h}{\sqrt{2 m k}}=\frac{h}{\sqrt{2 m e V}}\)

Here students can locate TS Inter 2nd Year Physics Notes 13th Lesson Atoms to prepare for their exam.

TS Inter 2nd Year Physics Notes 13th Lesson Atoms

→ J.J. Thomson thought that the positive charge of the atom is uniformly distributed through out the volume of the atom and the negatively charged electrons are embedded in it like seeds in a watermelon.

→ According to Rutherford the entire positive charge and most of the mass of the atom is concentrated in a small volume called nucleus. Electrons are revolving around the nucleus at some distance just as planets revolve around the sun.

→ Alpha particle scattering experiments on gold foil showed that size of nucleus is about 10^-14 to 10^-15 m and size of atom is nearly 10^-10 m.

→ Most of the atom is empty space. The electrons would be moving in certain orbits with some distance from nucleus just like planets around the sun.

→ Alpha particle scattering experiment :
Magnitude of force between α – particle and gold nuclie is F = \(\frac{1}{4 \pi \epsilon_o} \frac{(2 \mathrm{e})(\mathrm{Ze})}{\mathrm{r}^2}\) Where ‘r’ is the distance between α – particle and nucleus.
The magnitude and direction of force changes continuously as it approaches the nucleus.

→ Impact Parameter: It is the perpendicular distance of the initial velocity vector of a particle from centre of nucleus.
In case of head on collision impact parameter is minimum and α – particle rebounds back (θ = π). For a large impact parameter α – particle goes undeviated. The chance of head on collision is very small. It in turn suggested that mass of atom is much concentrated in a small volume.

→ Bohr postulates : Bohr model of hydrogen atom consists of three main postulates.

• Electrons in an atom could revolve in certain permitted stable orbits. Electrons revolving in these stable orbits do not emit or radiate any energy.
• The stable orbits are those whose orbital angular momentum is an integral multiple of h/ 2π.
  i. e., L = nh / 2π where n = 1, 2, 3, ……………… etc. (an integer.)
  These stable orbits are also called as non – radiating orbits.
• An electron may take a transition between non-radiating orbits. When electron transition takes place a photon of energy equals to the energy difference between initial and final states will be radiated.
  E = hv = E_i– E_j

→ Bohr radius (a₀): According to Bohr theory radius of the orbit, r = \(\frac{\mathrm{n}^2 \mathrm{~h}^2 \epsilon_0}{\pi \mathrm{me}^2}\) when n = 1. It is called first orbit. Radius of 1st orbit r₁ = \(\frac{h^2 \epsilon_0}{\pi \mathrm{me}^2}\) = 5.29 × 10^-11 m. This is called Bohr orbit a₀.
a₀ = \(\frac{h^2 \epsilon_0}{\pi \mathrm{me}^2}\) = 5.29 × 10^-11 m = 0.529 Å

→ Energy of orbit: From Bohr theory energy of the orbit E = –\(\frac{m e^4}{8 n^2 h^2 \epsilon_o^2}\)
Where – ve sign indicates the force of attraction between electron and nucleus.
For 1st orbit n = 1.
Its energy E₁ = -2.18 × 10^-18 J or
E₁ = – 13.6 eV.
For all other orbits their energy E = \(\frac{13.6}{n^2}\) eV
Note: The energy of an atom is least (i.e., it has maximum – ve value) when electron is revolving with n = 1 orbit. This energy state (n = 1) is called lowest state of the atom or ground state. For ground state of hydrogen atom E = – 13.6 eV.

→ Spectral series: From Bohr model electrons are permitted to transit between the energy levels while doing so they will absorb or release the exact amount of energy difference of the initial and final states.
∴ Energy absorbed or released E = hv = E_i – E_f
E = hv = \(\frac{\mathrm{hc}}{\lambda}=\frac{m \mathrm{e}^4}{8 \varepsilon_{\mathrm{o}} \mathrm{h}^2}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right]\) or
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right]\) where R is Rydberg’s constant R = 1.03 × 10⁷ / m

→ Lyman series: When electrons are jumping on to the first orbit from higher energy levels then that series of spectral lines emitted are called ”lyman series”.
In Lyman series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{n^2}\right]\) where n = 2, 3, …… etc

→ Balmer series : When electrons are jumping on to the second orbit from higher levels then that series of spectral lines are called “Balmer series”.
For Balmer series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{\mathrm{n}^2}\right]\) where n = 3,4,………. Spectral lines of Balmer series are in visible region.

→ Paschen series : When electrons are jump¬ing on to the 3rd orbit from higher energy levels then that series of spectral lines are called “Paschen series”.
For Paschen series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{\mathrm{n}^2}\right]\)
n = 4, 5………….. These spectral lines are in near infrared region.

→ Brackett series: When electrons are jump¬ing on to the 4th orbit from higher levels then that series of spectral lines are called “Brackett series”.
For Brackett series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{4^2}-\frac{1}{n^2}\right]\) where n = 5, 6, …………….
Brackett series are in middle infrared region.

→ Pfund series: When electrons are jumping on to the 5th orbit from higher energy levels then that series of spectral lines are called
“pfund series”.
For pfund series \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{5^2}-\frac{1}{\mathrm{n}^2}\right]\)
where n = 6, 7, ………… These spectral lines are in far infrared region.

Note : In spectral lines \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{\mathrm{n}_{\mathrm{i}}^2}-\frac{1}{\mathrm{n}_{\mathrm{f}}^2}\right]\)R
But \(\frac{1}{\lambda}\) = v/c

Frequency of spectral line v = Rc\(\left[\frac{1}{n_i^2}-\frac{1}{n_f^2}\right]\)

→ Ionisation potential : It is the amount of minimum energy required to release an ele-ctron from the outer most orbit of the nucleus.
From Bohr’s model energy of the orbit is the ionisation energy of electron in that orbit.
Ex: Energy of 1st orbit in hydrogen is 13.6 eV.
Practically ionisation potential of hydro-gen is 13.6 eV.
Note : The success of Bohr atom model is in the prediction of ionisation energy of orbits.

→ Force between ‘a’ particle and positively charged nucleus
F = \(\frac{1}{4 \pi \varepsilon_o} \frac{2 \mathrm{e}(\mathrm{Ze})}{\mathrm{r} 2}=\frac{\mathrm{Ze}^2}{2 \pi \varepsilon_0 r^2}\)

→ Kinetic energy of α – particle,
K = \(\frac{2 Z \mathrm{e}^2}{4 \pi \varepsilon_{\mathrm{o}} \mathrm{d}}=\frac{Z \mathrm{e}^2}{2 \pi \varepsilon_{\mathrm{o}} \mathrm{d}}\)

→ Distance of closest approach d = \(\frac{\mathrm{Ze}^2}{2 \pi \varepsilon_0 \mathrm{k}}\)

→ For an electron moving in the orbit of hydrogen atom = \(\frac{m v^2}{r}=\frac{1}{4 \pi \varepsilon_o} \frac{Z^2}{r^2}\)

→ For an atom of atomic number ‘Z’, \(\frac{\mathrm{mv}^2}{\mathrm{r}}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{Ze}^2}{\mathrm{r}^2}\)

→ Relation between orbit radius and velocity in hydrogen atom is r = e² / 4πε₀
mv² = \(\frac{1}{4 \pi \varepsilon_o}\) where k = \(\frac{1}{4 \pi \varepsilon_o}\) = 9 × 10⁹

→ In hydrogen atom .
(1) Kinetic energy K = \(\frac{1}{2}\)mv²

(ii) Potential energy U = \(\frac{\mathrm{e}^2}{8 \pi \varepsilon_o \mathrm{r}}=\frac{m \mathrm{e}^4}{8 \mathrm{n}^2 \mathrm{~h}^2 \varepsilon_o^2}\)
= \(-\frac{e^2}{4 \pi \varepsilon_o r}\) (-ve sigh for force of attraction)

(iii) Total energy E = K + U
= \(-\frac{e^2}{8 \pi \varepsilon_o r}=\frac{-m e^4}{8 n^2 h^2 \varepsilon_o^2}\)

(iv) Velocity of electron in orbit v = e/\(\sqrt{4 \pi \varepsilon_o \mathrm{mr}}\)

→ Spectral series: Wavelengths of spectral series are given by \(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right)\)
where n₁ and n₂ are the number of orbits between which electron transition takes place.
Energy radiated In transition E = hv = E₂ – E₁
In Bohr atom model.
Angular momentum of orbital L = mvr = \(\frac{\mathrm{nh}}{2 \pi}\)
radius of nth orbit r_n = \(\frac{\mathrm{nh}}{2 \pi}\)

Velocity of electron in nth orbit
V_n = e/\(\sqrt{4 \pi \varepsilon_o m r_n}\)
or v_n = \(\frac{1}{\mathrm{n}} \frac{\mathrm{e}^2}{4 \pi \varepsilon_{\mathrm{o}}} \frac{1}{(\mathrm{~h} / 2 \pi)}\)
or
r_n = \(\frac{\mathrm{n}^2 \mathrm{~h}^2 \varepsilon_0}{\pi \mathrm{me}^4}\)
Bohr radius a₀ = \(\frac{h^2 \varepsilon_o}{\pi m e^4}\) = 5.29 × 10^-11 m

Energy of nth orbit
E_n = \(\frac{-\mathrm{me}^4}{8 \mathrm{n}^2 \mathrm{~h}^2 \varepsilon_{\mathrm{o}}^2}=\frac{-2.18 \times 10^{-18}}{\mathrm{n}^2}\)J = \(\frac{-13.6}{n^2}\)eV
Rydberg’s constant R = \(\frac{m \mathrm{e}^4}{8 \varepsilon_o^2 h^3 \mathrm{c}}\)
= 1.03 × 10⁷ m^-1

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Circles Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Circles Important Questions Short Answer Type

Question 1.
If a point P is moving such that the lengths of tangents drawn from P to the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 are in the ratio 2 : 3, then find the equation of the locus of P. [(AP) Mar. ’19, (TS) ’17]
Solution:
Let P(x₁, y₁) be a point on the locus and S = x² + y² – 4x – 6y – 12 = 0
S’ = x² + y² + 6x + 18y + 26 = 0 be the given circles.

Question 2.
If a point P is moving such that the lengths of tangents drawn from P to x² + y² – 2x + 4y – 20 = 0 and x² + y² – 2x – 8y + 1 = 0 are in the ratio 2 : 1, then show that the equation of locus of P is x² + y² – 2x – 12y + 8 = 0.
Solution:
Let P(x, y) be a point on the locus and
S = x² + y² – 2x + 4y – 20 = 0
S’ = x² + y² – 2x – 8y + 1 = 0 be the given circles.
Length of tangent from P to S = 0 is
PA = \(\sqrt{S_{11}}=\sqrt{x^2+y^2-2 x+4 y-20}\)
Length of tangent from P to S’ = 0 is
PB = \(\sqrt{\mathrm{S}_{11}^{\prime}}=\sqrt{\mathrm{x}^2+\mathrm{y}^2-2 \mathrm{x}-8 \mathrm{y}+1}\)
Given condition is PA : PB = 2 : 1
\(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{2}{1}\)
⇒ PA = 2PB
⇒ \(\sqrt{x^2+y^2-2 x+4 y-20}\) = \(2 \sqrt{x^2+y^2-2 x-8 y+1}\)
squaring on both sides
⇒ x² + y² – 2x + 4y – 20 = 4(x² + y² – 2x – 8y + 1)
⇒ x² + y² – 2x + 4y – 20 – 4x² – 4y² + 8x + 32y – 4 = 0
⇒ -3x² – 3y² + 6x + 36y – 24 = 0
⇒ x² + y² – 2x – 12y + 8 = 0
The equation of locus of P is x² + y² – 2x – 12y + 8 = 0.

Question 3.
Find the equations of the tangent to the circle x² + y² – 4x + 6y – 12 = 0 which are parallel to x + y – 8 = 0. (Mar. ’01)
Solution:
Given equation of the circle is x² + y² – 4x + 6y – 12 = 0

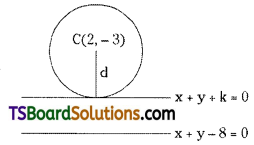
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -2, f = 3, c = -12
Centre C = (-g, -f) = (2, -3)
Radius r = \(\sqrt{g^2+\mathrm{f}^2-\mathrm{c}}=\sqrt{4+9+12}\) = 5
Given equation of the straight line is x + y – 8 = 0
The equation of the tangent parallel to x + y – 8 = 0 is
x + y + k = 0 ……….(1)
Since eq. (1) is a tangent to the given circle then r = d.
r = \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)
⇒ 5 = \(\frac{|1(2)+1(-3)+\mathbf{k}|}{\sqrt{(1)^2+(1)^2}}\)
⇒ 5 = \(\frac{|2-3+\mathbf{k}|}{\sqrt{2}}\)
⇒ 5√2 = |k – 1|
⇒ k – 1 = ±5√2
⇒ k = 1 ± 5√2
Substitute the value of ‘k’ in eq. (1)
x + y + 1 ± 5√2 = 0

Question 4.
Show that x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0 and find its point of contact.
Solution:
Given equation of the circle is x² + y² – 3x + 7y + 14 = 0

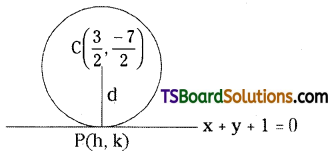
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0, we get

Given the equation of the line is x + y + 1 = 0.
Now, d = The perpendicular distance from the centre C\(\left(\frac{3}{2}, \frac{-7}{2}\right)\) to the line x + y + 1 = 0.

Since r = d then, the line x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0.
Let P(h, k) be the point of contact.
Now, P(h, k) is the foot of the perpendicular drawn from C = \(\left(\frac{3}{2}, \frac{-7}{2}\right)\) to the line x + y + 1 = 0

∴ The point of contact is P(2, -3).

Question 5.
Show that the points (1, 1), (-6, 0), (-2, 2), and (-2, -8) are concyclic and find the equation of the circle on which they lie. [(AP) Mar. ’19; May ’17]
Solution:
Let, the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 …….(1)
Since, (1) passes through point (1, 1)
1² + 1² + 2g(1) + 2f(1) + c = 0
2 + 2g + 2f + c = 0
2g + 2f + c = -2 ……(2)
Since, (1) passes through the point (-6, 0)
(-6)² + 0² + 2g(-6) + 0 + c = 0
36 + c – 12g = 0
-12g + c = -36 …….(3)
Since, (1) passes through the point (-2, 2)
(-2)² + (2)² + 2g(-2) + 2f(2) + c = 0
4 + 4 – 4g + 4f + c = 0
-4g + 4f + c = -8 ……..(4)
From (2) and (3)

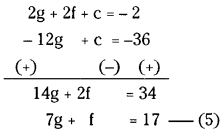
From (3) and (4)

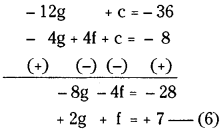
Solving (5) and (6)

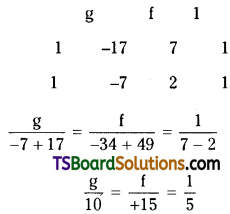
g = 2, f = 3
Substitute the values of g, f in (2)
2(2) + 2(3) + c = -2
4 + 6 + c = -2
10 + c = -2
c = -12
Now, substitute the values of g, f, c in (1)
∴ The equation of the required circle is
x² + y² + 2(2) x + 2(3) y – 12 = 0
x² + y² + 4x + 6y – 12 = 0 ………(7)
Now, substituting the point (-2, -8) in (7)
(-2)² + (-8)² + 4(-2) + 6(-8) – 12 = 0
4 + 64 – 8 – 48 – 12 = 0
68 – 68 = 0
0 = 0
∴ Given points are concyclic.
∴ Required equation of the circle is x² + y² + 4x + 6y – 12 = 0

Question 6.
Find the equations of the tangents to the circle x² + y² + 2x – 2y – 3 = 0 which are perpendicular to 3x – y + 4 = 0.
Solution:
Given equation of the circle is x² + y² + 2x – 2y – 3 = 0

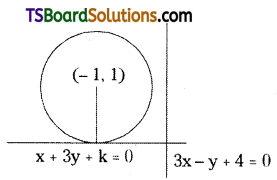
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = 1, f = -1, c = -3,
Centre of the circle C(-g, -f) = (-1, 1)
The radius of the circle
r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(-1)^2+(1)^2+3}\)
= √5
Given the equation of the straight line is 3x – y + 4 = 0
The equation of the straight line perpendicular to 3x – y + 4 = 0 is
x + 3y + k = 0 ……..(1)
Since (1) is the tangent to the given circle then r = d
√5 = \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)

The equations of the tangents are from (1),
x + 3y – 2 ± 5√2 = 0

Question 7.
Show that the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0 and finds its point of contact. (May ’10)
Solution:
Given equation of the circle is x² + y² – 4x – 8y + 7 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
we get g = -2, f = -4, c = 7
Let the given point P(x₁, y₁) = (-1, 2)
The equation of the tangent is S1 = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-1) + y(2) – 2(x – 1) – 4(y + 2) + 7 = 0
⇒ -x + 2y – 2x + 2 – 4y – 8 + 7 = 0
⇒ -3x – 2y + 1 = 0
⇒ 3x + 2y – 1 = 0

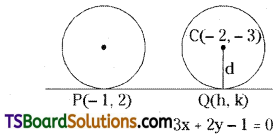
Given equation of the circle is x² + y² + 4x + 6y = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = 2, f = 3, c = 0
Centre C(-g, -f) = (-2, -3)
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9}\)
= √13
Now d = The perpendicular distance from the centre C = (-2, -3) to the line 3x + 2y – 1 = 0

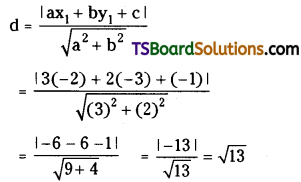
Since r = d, the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0.
Let Q(h, k) be the point of contact.
Now, Q(h, k) is the foot of the perpendicular drawn from centre C(-2, -3) to the line 3x + 2y – 1 = 0.

∴ The point of contact Q(h, k) = (1, -1).

Question 8.
Find the angle between the tangents drawn from (3, 2) to the circle x² + y² – 6x + 4y – 2 = 0. (Mar. ’12)
Solution:
Given the equation of the circle is x² + y² – 6x + 4y – 2 = 0.

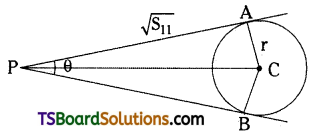
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -3, f = 2, c = -2
Radius r = \(\sqrt{9+4+2}=\sqrt{15}\)
Let the given point P(x₁, y₁) = (3, 2)
Length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

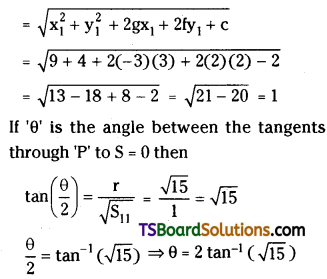
Question 9.
Find the locus of ‘P’ where the tangent is drawn from ‘P’ to x² + y² = a² are perpendicular to each other.
Solution:
Given the equation of the circle is x² + y² = a²
Radius r = a

Let P(x₁, y₁) be any point on the locus.
Length of the tangent = \(\sqrt{\mathrm{S}_{11}}\) = \(\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2-\mathrm{a}^2}\)
Given that angle between the tangents θ = 90°
If ‘θ’ is the angle between the tangents through ‘P’ to the given circle then
\(\tan \left(\frac{\theta}{2}\right)=\frac{r}{\sqrt{S_{11}}}\)

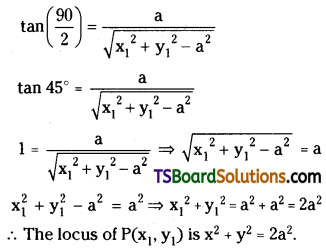
Question 10.
Find the chord length intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0. [(TS) Mar. ’16]
Solution:
Given equation of the circle is x² + y² – 8x – 2y – 8 = 0

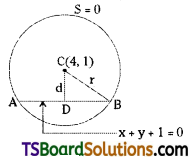
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0,
we get g = -4, f = -1, c = -8
Centre of the circle C = (-g, -f) = (4, 1)
Radius r =\(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{(-4)^2+(-1)^2+8}\)
= 5
Given equation of the straight line is x + y + 1 = 0
Now d = perpendicular distance from the centre C(4, 1) to the chord x + y + 1 = 0

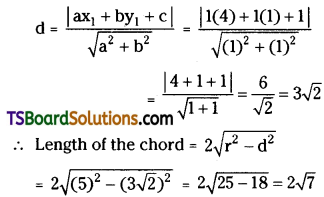
Question 11.
Find the chord length intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3. [(TS) Mar. ’20; (AP) Mar. ’18, May ’16, Mar. ’13]
Solution:
Given equation of the circle is x² + y² – x + 3y – 22 = 0

Question 12.
Find die length of the chord formed by x² + y² = a² on the line x cos α + y sin α = P. [(TS) Mar. ’16]
Solution:
Given equation of the circle is x² + y² – a² = 0

Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 0, f = 0, c = -a²
Centre of the circle C(-g, -f) = (0, 0)
Radius of the circle r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(0)^2+(0)^2+a^2}\)
= a
Given the equation of the straight line is x cos α + y sin α – P = 0
Now d = perpendicular distance from the centre C(0,0) to the chord x cos α + y sin α – P = 0

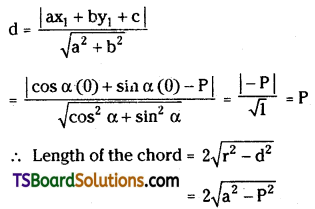
Question 13.
Find the equation of the circle with centre (-2, 3) cutting a chord length 2 units on 3x + 4y + 4 = 0. (Mar. ’11)
Solution:
Given that centre C(h, k) = (-2, 3)
Given the equation of the straight line is 3x + 4y + 4 = 0
Now d = The perpendicular distance from the centre C(-2, 3) to the line 3x + 4y + 4 = 0.

Given that the length of the chord = 2
\(2 \sqrt{\mathrm{r}^2-\mathrm{d}^2}\) = 2
⇒ \(\sqrt{\mathrm{r}^2-\mathrm{d}^2}\) = 1
⇒ r² – d² = 1
⇒ r² – 2² = 1
⇒ r² – 4 = 1
⇒ r² = 5
⇒ r = √5
The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x + 2)² + (y- 3)² = (√5)²
⇒ x² + 4 + 4x + y² + 9 – 6y = 5
⇒ x² + y² + 4x – 6y + 8 = 0

Question 14.
Find the area of the triangle formed by the normal at (3, -4) to the circle x² + y² – 22x – 4y + 25 = 0 with the coordinate axis. [Mar. ’18 (TS)]
Solution:
Given circle is x² + y² – 22x – 4y + 25 = 0
Compare with x² + y² + 2gx + 2fy + c = 0 then
we get 2g = -22 ⇒ g = -11
2f = -4 ⇒ f = -2, c = 25
centre c(-g, -f) = c(11, 2)

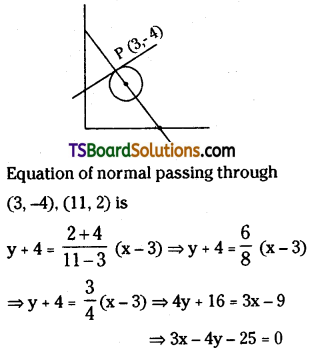
The area of the triangle formed by the normal with the coordinate axis = \(\frac{c^2}{2|a b|}\)
= \(\frac{(-25)^2}{2|3(-4)|}\)
= \(\frac{625}{24}\) sq units

Question 15.
Find the mid point of the chord intercepted by x² + y² – 2x – 10y + 1 = 0 on the line x – 2y + 7 = 0.
Solution:
Given equation of the circle is x² + y² – 2x – 10y + 1 = 0

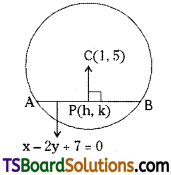
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
we get, g = -1, f = -5, c = 1
Centre of the circle, C = (-g, -f) = (1, 5)
Given equation of the straight line is x – 2y + 7 = 0
Comparing this equation with ax + by + c = 0,
we get a = 1, b = -2, c = 7
Let P(h, k) is the midpoint of the chord x – 2y + 7 = 0
Now P(h, k) is the foot of the perpendicular from centre C(1, 5) on the chord x – 2y + 7 = 0

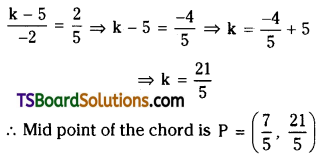
Question 16.
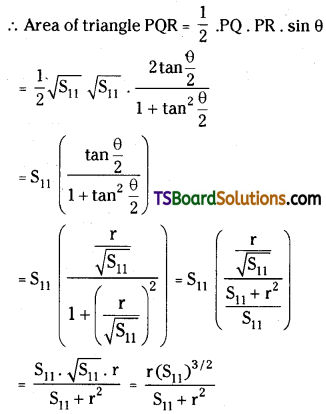
Show that the area of the triangle formed by the two tangents through P(x₁, y₁) to the circle S = x² + y² + 2gx + 2fy + c = 0 and the chord of contact of ‘P’ with respect to S = 0 is \(\frac{\mathbf{r}\left(\mathbf{S}_{11}\right)^{3 / 2}}{\mathbf{S}_{11}+\mathbf{r}^2}\), where ‘r’ is the radius of the circle.
Solution:
If θ is the angle between the tangents ‘P’ to S = 0, then
\(\tan \left(\frac{\theta}{2}\right)=\frac{r}{\sqrt{S_{11}}}\)

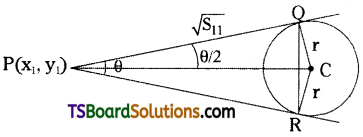
Let Q, R be the chord of the contact from ‘P’ to the circle.
Let PA be the ⊥r from P to QR.

Question 17.
Find the pole of the line x + y + 2 = 0 w.r.t the circle x² + y² – 4x + 6y – 12 = 0. [(AP) Mar. ’17, May ’15]
Solution:
Given equation of the circle x² + y² – 4x + 6y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = 3, c = -12
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9+12}\)
= 5
Given equation of the straight line is x + y + 2 = 0
Comparing this equation with lx + my + n = 0,
we get l = 1, m = 1, n = 2
The pole of lx + my + n = 0 w.r.t x² + y² + 2gx + 2fy + c = 0 is

Question 18.
Find the pole of the line 3x + 4y – 45 = 0 w.r.t the circle x² + y² – 6x – 8y + 5 = 0. [(AP) Mar. ’16]
Solution:
Given equation of the circle x² + y² – 6x – 8y + 5 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -3, f = -4, c = 5
Radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{9+16-5}\)
= √20
Given the equation of the straight line is 3x + 4y – 45 = 0
Comparing the given equation with lx + my + n = 0,
we get l = 3, m = 4, n = -45
The pole of lx + my + n = 0 w.r.t x² + y² + 2gx + 2fy + c = 0 is

Question 19.
Show that the lines 2x + 3y + 11 = 0, 2x – 2y – 1 = 0 are conjugate w.r.t the circle x² + y² + 4x + 6y + 12 = 0.
Solution:
Given equation of the circle x² + y² + 4x + 6y + 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = 2, f = 3, c = 12
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9-12}\)
= 1
Given equations of the straight lines are
2x + 3y + 11 = 0 …….(1)
2x – 2y – 1 = 0 ………(2)
Comparing (1) with l₁x + m₁y + n₁ = 0
we get l₁ = 2, m₁ = 3, n₁ = 11
Comparing (2) with l₂x + m₂y + n₂ = 0
we get l₂ = 2, m₂ = -2, n₂ = -1
Now (l₁g + m₁f – n₁) (l₂g + m₂f – n₂)
= [2(2) + 3(3) – 11] [2(2) + 3(-2) + 1]
= (4 + 9 – 11) (4 – 6 + 1)
= 2(-1)
= -2
r² (l₁l₂ + m₁m₂) = (1)² [2(2) + 3(-2)]
= 1(4 – 6)
= -2
∴ (l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = r² (l₁l₂ + m₁m₂)
∴ Given lines are conjugate w.r.t given circle.

Question 20.
Find the value of ‘k’ if x + y – 5 = 0 and 2x + ky – 8 = 0 are conjugate with respect to the circle x² + y² – 2x – 2y – 1 = 0. [(TS) May ’18]
Solution:
Given equation of the circle is x² + y² – 2x – 2y – 1 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -1, f = -1, c = -1
Radius r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
= \(\sqrt{1+1+1}\)
= √3
Given equations of the straight lines are
x + y – 5 = 0 ………(1)
2x + ky – 8 = 0 ……..(2)
Comparing (1) with l₁x + m₁y + n₁ = 0
we get l₁ = 1, m₁ = 1, n₁ = -5
Comparing (2) with l₂x + m₂y + n₂ = 0
we get l₂ = 2, m₂ = k, n₂ = -8
Since given lines are conjugate w.r.t given circle, then
(l₁g + m₁f – n₁) (l₂g + m₂f – n₂) = r² (l₁l₂ + m₁m₂)
⇒ [1(-1) + 1(-1) + 5] [2(-1) + k(-1) + 8] = (√3)2 [1(2) + 1(k)]
⇒ (-1 – 1 + 5)(-2 – k + 8) = 3(2 + k)
⇒ 3(-k + 6) = 3(k + 2)
⇒ -k + 6 = k + 2
⇒ 2k = 4
⇒ k = 2

Question 21.
Find the condition that the tangents drawn from (0, 0) to S = x² + y² + 2gx + 2fy + c = 0 be perpendicular to each other. [(TS) May ’16]
Solution:
Given equation of the circle is S = x² + y² + 2gx + 2fy + c = 0

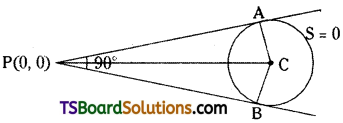
Centre, C = (-g, -f)
Radius, r = \(\sqrt{\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}}\)
Let, the given point P(x₁, y₁) = (0, 0)
The angle between the tangents, θ = 90°
The length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

Question 22.
If the abscissae of points A, B are the roots of the equation x² + 2ax – b² = 0 and ordinates of A, B are roots of y² + 2py – q² = 0, then find the equation of a circle for which \(\overline{\mathbf{A B}}\) is a diameter. (Mar. ’14)
Solution:
Let A (x₁, y₁)( B (x₂, y₂) are the two given points.
Since x₁, x₂ are the roots of the quadratic equation x² + 2ax – b² = 0 then
sum of the roots = \(\frac{-b}{a}\)
x₁ + x₂ = \(\frac{-2 \mathrm{a}}{1}\) = -2a
Product of the roots = \(\frac{c}{a}\)
x₁x₂ = \(\frac{-b^2}{1}\) = -b²
Since y₁, y₂ are the roots of the quadratic equation y² + 2py – q² = 0 then
sum of the roots = \(\frac{-b}{a}\)
y₁ + y₂ = \(\frac{-2 p}{1}\) = -2p
Product of the roots = \(\frac{c}{a}\)
y₁y₂ = \(\frac{-\mathrm{q}^2}{1}\) = -q²
The equation of a circle for which \(\overline{\mathbf{A B}}\) is a diameter is
(x – x₁)(x – x₂) + (y – y₁)(y – y₂) = 0
⇒ x² – xx₂ – xx₁ + x₁x₂ + y² – yy₁ – yy₂ + y₁y₂ = 0
⇒ x² – x(x₁ + x₂) + x₁x₂ + y² – y(y₁ + y₂) + y₁y₂ = 0
⇒ x² – x(-2a) + (-b2) + y² – y(-2p) + (-q2) = 0
⇒ x² + y² + 2ax + 2py – b² – q² = 0

Question 23.
Find the equation of the circle which touches the x-axis at a distance of 3 from the origin and make an intercept of length 6 on the y-axis.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)

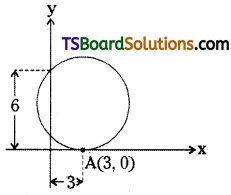
Since (1) meets the x-axis at A(3, 0)
∴ Point A(3, 0) lies on the circle (1), then
(3)² + (0)² + 2g(3) + 2f(0) + c = 0
⇒ 9 + 6g + c = 0
⇒ 6g + c = -9 ……..(2)
Since, the circle (1) touches the x-axis, then
g² = c …….(3)
From (2) and (3)
6g + g² = – 9
⇒ g² + 6g + 9 = 0
⇒ (g + 3)² = 0
⇒ g + 3 = 0
⇒ g = -3
Now, substitute the value of g in (3), and we get
(-3)² = c
⇒ c = 9
Given that the intercept on the y-axis made by (1) is 6
\(2 \sqrt{f^2-c}\) = 6
⇒ \(\sqrt{\mathrm{f}^2-\mathrm{c}}\) = 3
⇒ \(\sqrt{\mathrm{f}^2-9}\) = 3
⇒ f² – 9 = 9
⇒ f² = 18
⇒ f = ±3√2
Substitute the values of g, f, c in (1)
∴ The required equation of the circle is x² + y² + 2(-3)x + 2(±3√2)y + 9 = 0
⇒ x² + y² – 6x ± 6√2y + 9 = 0

Question 24.
Find the equation of the circle passing through (0, 0) and making intercepts 4, 3 on the x, y-axis respectively.
Solution:
Let the equation of the required circle is
x² + y² + 2gx + 2fy + c = 0 ………(1)
Since (1) passes through the point (0, 0), then
(0)² + (0)² + 2g(0) + 2f(0) + c = 0
∴ c = 0
Given that the intercept on the x-axis made by (1) = 4

Now, substitute the values of g, f, c in (1)
The equation of the required circle is
x² + y² + 2(±2)x + 2(±\(\frac{3}{2}\))y + 0 = 0
⇒ x² + y² ± 4x ± 3y = 0

Question 25.
Show that the locus of the point of intersection of the lines x cos α + y sin α = a, x sin α – y cos α = b (α is a parameter) is a circle.
Solution:
Given equations of the straight lines are
x cos α + y sin α = a …….(1)
x sin α – y cos α = b …….(2)
Now (1)² + (2)²
⇒ (x cos α + y sin α)² + (x sin α – y cos α)² = a² + b²
⇒ x² cos²α + y² sin²α + 2xy sin α cos α + x² sin²α + y² cos²α – 2xy sin α cos α = a² + b²
⇒ x² (cos²α + sin²α) + y² (sin²α + cos²α) = a² + b²
⇒ x² (1) + y² (1) = a² + b²
∴ x² + y² = a² + b²
∴ The locus of the point of intersection of the given line is x² + y² = a² + b²
It represents a circle.

Question 26.
If y = mx + c and x² + y² = a²
(i) Intersect at A and B
(ii) AB = 2λ, then show that c² = (1 + m²) (a² – λ²)
Solution:
Given the equation of the circle is x² + y² = a²

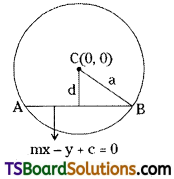
Comparing this equation with x² + y² = r², then centre of the circle C = (0, 0)
The radius of the circle r = a
Given the equation of the straight line is mx – y + c = 0
Now, d = the perpendicular distance from the centre C(0, 0) to the line mx – y + c = 0

Question 27.
Find the equation of the circle with centre (2, 3) and touch the line 3x – 4y + 1 = 0.
Solution:
Given, centre C(h, k) = (2, 3)

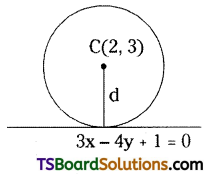
Given the equation of the straight line is 3x – 4y + 1 = 0
Since, the line 3x – 4y + 1 = 0 touches the required circle, then the line 3x – 4y + 1 = 0 is a tangent to the required circle.
∴ Radius r = The perpendicular distance from the centre C(2, 3) to the tangent 3x – 4y + 1 = 0

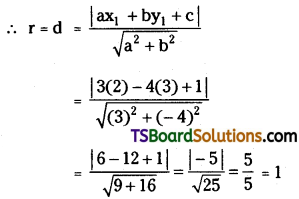
∴ The equation of the required circle is (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = (1)²
⇒ x² + 4 – 4x + y² + 9 – 6y = 1
⇒ x² + y² – 4x – 6y + 12 = 0

Question 28.
Find the equation of the tangent at the point 30° (parametric value of θ) of the circle x² + y² + 4x + 6y – 39 = 0.
Solution:
Given equation of the circle is x² + y² + 4x + 6y – 39 = 0
Comparing the given equation with x² + y² + 2gx + 2fy + c = 0
We get g = 2, f = 3, c = -39
Radius r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(2)^2+(3)^2+39}\)
= 2√13
The given point θ = 30°
∴ The equation of the tangent at the point θ of the given circle is (x + g) cos θ + (y + f) sin θ = r
⇒ (x + 2) cos 30° + (y + 3) sin 30° = 2√13
⇒ (x + 2) . \(\frac{\sqrt{3}}{2}\) + (y + 3) . \(\frac{1}{2}\) = 2√13
⇒ √3x + 2√3 + y + 3 = 4√13
⇒ √3x + y + 2√3 + 3 – 4√13 = 0

Question 29.
Find the equation of the tangent to x² + y² – 2x + 4y = 0 at (3, -1). Also, find the equation of tangent parallel to it. [(TS) May ’17]
Solution:
Given equation of the circle is x² + y² – 2x + 4y = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get g = -1, f = 2, c = 0
The given point P(x₁, y₁) = (3, -1)
∴ The equation of the tangent at P is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(-1) – 1(x + 3) + 2(y – 1) + 0 = 0
⇒ 3x – y – x – 3 + 2y – 2 = 0
⇒ 2x + y – 5 = 0
Centre of the circle, C = (-g, -f) = (1, -2)

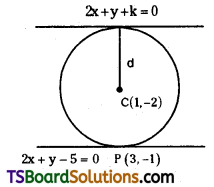
Radius of the circle, r = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(-1)^2+(2)^2+0}\)
= √5
The equation of the straight line parallel to the tangent 2x + y – 5 = 0 is
2x + y + k = 0 …….(1)
If (1) is a tangent to the given circle when r = d

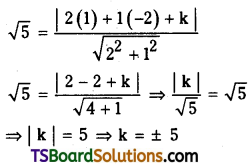
The equations of tangents to the circle are from (1)
2x + y ± 5 = 0
One of these equations namely 2x + y – 5 = 0 is the tangent at (3, -1).
The tangent parallel to 2x + y – 5 = 0 is 2x + y + 5 = 0.

Question 30.
If 4x – 3y + 7 = 0 is a tangent to the circle represented by x² + y² – 6x + 4y – 12 = 0 then find the point of contact.
Solution:
Given equation of the circle is x² + y² – 6x + 4y – 12 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get, g = -3, f = 2, c = -12
Centre of the circle, C = (-g, -f) = (3, -2)
Given equation of the tangent is 4x – 3y + 7 = 0
Let the point of contact be P = (h, k)

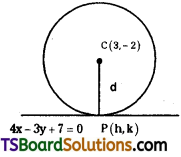
Now, P(h, k) is the foot of the perpendicular from the centre, C(3, -2) to the tangent 4x – 3y + 7 = 0

Question 31.
Find the equation of the normal to the circle x² + y² – 4x – 6y + 11 = 0 at (3, 2). Also, find the other point where the normal meets the circle.
Solution:
Given equation of the circle is x² + y² – 4x – 6y + 11 = 0

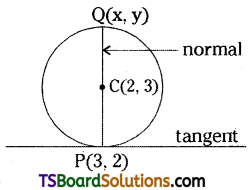
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -3, c = 11
Given point P(x₁, y₁) = (3, 2)
Centre of the circle C(-g, -f) = (2, 3)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) + (- 2) (x + 3) – 3(y + 2) + 11 = 0
⇒ 3x + 2y – 2x – 6 – 3y – 6 + 11 = 0
⇒ x – y – 1 = 0
Slope of the tangent at P is m = \(\frac{-1}{-1}\) = 1
Slope of the normal at P is \(\frac{-1}{m}=\frac{-1}{1}\) = -1
∴ The equation of the normal at P is
y – y₁ = \(\frac{-1}{m}\) (x – x₁)
⇒ y – 2 = -1(x – 3)
⇒ y – 2 = -x + 3
⇒ x + y – 5 = 0
Other point of the normal Q = (x, y)
The centre of the circle is the midpoint of P and Q (point of intersection of normal and circle)
∴ C(2, 3) = Midpoint of PQ

∴ The normal at (3, 2) meets the circle at (1, 4).

Question 32.
Find the equation of the normal to the circle x² + y² – 10x – 2y + 6 = 0 at (3, 5). Also, find the other point where the normal meets the circle.
Solution:
Given equation of the circle is x² + y² – 10x – 2y + 6 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -5, f = -1, c = 6
The given point P(x₁, y₁) = (3, 5)
∴ The equation of the tangent at P is S₁ = 0
⇒ xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(5) + (-5) (x + 3) + (-1) (y + 5) + 6 = 0
⇒ 3x + 5y – 5x – 15 – y – 5 + 6 = 0
⇒ -2x + 4y – 14 = 0
⇒ x – 2y + 7 = 0
The slope of the tangent at P is m = \(\frac{-\mathrm{a}}{\mathrm{b}}=\frac{-1}{-2}=\frac{1}{2}\)
The slope of the normal at P is \(\frac{-1}{\mathrm{~m}}=\frac{-1}{\frac{1}{2}}\) = -2
∴ The equation of the normal at P(3, 5) is
\(\mathrm{y}-\mathrm{y}_1=\frac{-1}{\mathrm{~m}}\left(\mathrm{x}-\mathrm{x}_1\right)\)
⇒ y – 5 = -2(x – 3)
⇒ y – 5 = -2x + 6
⇒ 2x + y – 1 = 0

Question 33.
Find the locus of P, where the tangents drawn from P to x² + y² = a² include an angled α.
Solution:
Given the equation of the circle is x² + y² = a²

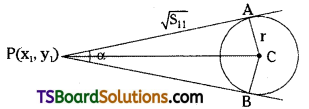
Comparing this equation with x² + y² = r²
We get r = a
Let P(x₁, y₁) be a point on the locus.
The length of the tangent = \(\sqrt{\mathrm{S}_{11}}\)

Question 34.
If ax + by + c = 0 is polar of (1, 1) w.r.t x² + y² – 2x + 2y + 1 = 0 and HCF of a, b, c is equal to one, then find a² + b² + c².
Solution:
Given equation of the circle is x² + y² – 2x + 2y + 1 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0,
We get g = -1, f = 1, c = 1
Let, the given point P(x₁, y₁) = (1, 1)
The equation of polar of (1, 1) w.r. t to the given circle is S₁ = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(1) – 1(x + 1) + 1(y + 1) + 1 = 0
⇒ x + y – x – 1 + y + 1 + 1 = 0
⇒ 2y + 1 = 0
Given equation of the polar is ax + by + c = 0, then
a = 0, b = 2, c = 1
The H.C.F of a, b, c is equal to ‘1’.
Now a² + b² + c² = (0)² + (2)² + (1)²
= 0 + 4 + 1
= 5

Question 35.
If the polar of the points on the circle x² + y² = a² with respect to the circle x² + y² = b² touches the circle x² + y² = c², then prove that a, b, c are in Geometric Progression.
Solution:
Given the equation of the first circle is x² + y² = a²

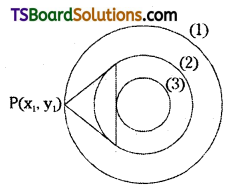
Let P(x₁, y₁) be any point on the circle x² + y² = a², then
\(\mathrm{x}_1^2+\mathrm{y}_1^2=\mathrm{a}^2\) ……….(1)
The equation of the second circle is x² + y² = b²
The polar of P(x₁, y₁) w.r.t the second circle x² + y² = b² is S₁ = 0
xx₁ + yy₁ – b² = 0 ……..(2)
The equation of the third circle is x² + y² = c²
Centre C = (0, 0); Radius r = c
Since (2) is a tangent to the circle x² + y² = c² then r = d
c = \(\frac{\left|\mathrm{x}_1(0)+\mathrm{y}_1(0)-\mathrm{b}^2\right|}{\sqrt{\mathrm{x}_1^2+\mathrm{y}_1^2}}\)
⇒ c = \(\frac{\left|-b^2\right|}{\sqrt{a^2}}\)
⇒ c = \(\frac{\mathrm{b}^2}{\mathrm{a}}\)
⇒ b² = ac
∴ a, b, c are in geometric progression.

Question 36.
Find the slope of the polar of (1, 3) with respect to the circle x² + y² – 4x – 4y – 4 = 0. Also, find the distance from the centre of it.
Solution:
Given equation of the circle is x² + y² – 4x – 4y – 4 = 0
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
We get g = -2, f = -2, c = -4
Centre of the circle C = (-g, -f) = (2, 2)
Let the given point be P(x₁, y₁) = (1, 3)
The equation of polar of (1, 3) w.r.t the given circle is S1 = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(1) + y(3) – 2(x + 1) – 2(y + 3) – 4 = 0
⇒ x + 3y – 2x – 2 – 2y – 6 – 4 = 0
⇒ -x + y – 12 = 0
⇒ x – y + 12 = 0
The slope of the polar is m = \(\frac{-\mathrm{a}}{\mathrm{b}}=\frac{-1}{-1}\) = 1
The perpendicular distance from the centre C(2, 2) to the polar x – y + 12 = 0 is

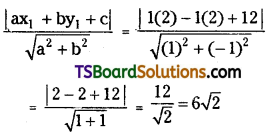
Question 37.
Show that, four common tangents can be drawn for the circles given by x² + y² – 14x + 6y + 33 = 0 and x² + y² + 30x – 2y + 1 = 0 and find the internal and external centres of similitude. [(TS) Mar. ’19]
Solution:
Given equations of the circles are
x² + y² – 14x + 6y + 33 = 0 ……..(1)
x² + y² + 30x – 2y + 1 = 0 ………(2)
For the circle (1), Centre C₁ = (7, -3)

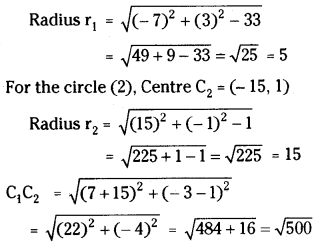
Now r₁ + r₂ = 5 + 15 = 20 = √400
∴ C₁C₂ > r₁ + r₂
∴ The given circles are each circle lies completely outside the other circle.
∴ No.of common tangents = 4

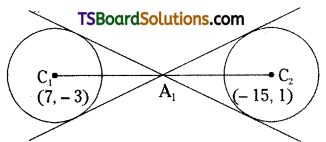
The internal centre of similitude A₁ internally divides C₁C₂ in the ratio r₁ : r₂ (5 : 15 = 1 : 3).
∴ The internal centre of similitude

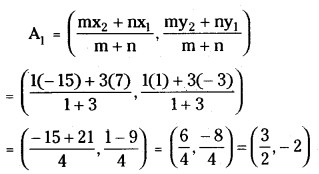
The external centre of similitude A₂ divides C₁C₂ in the ratio r₁ : r₂ (5 : 15 = 1 : 3) externally.

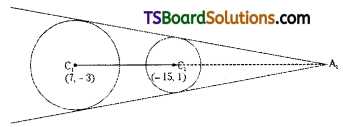
∴ The external centre of similitude

Question 38.
If a point P is moving such that the lengths of the tangent drawn from ‘P’ to the circle x² + y² + 8x + 12y + 15 = 0 and x² + y² – 4x – 6y – 12 = 0 are equal, then find the equation of the locus of P. (Mar. ’09)
Solution:
Given equations of the circles are
x² + y² + 8x + 12y + 15 = 0
x² + y² – 4x – 6y – 12 = 0

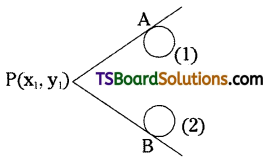
Let P(x₁, y₁) be any point on the locus.
PA, PB be the lengths of the tangent from P to the circles (1) & (2) respectively.
Given condition is PA = PB

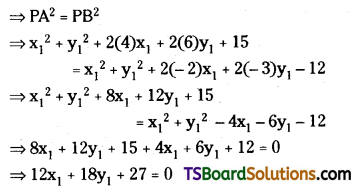
The equation of the locus of ‘P’ is 12x + 18y + 27 = 0
⇒ 4x + 6y + 9 = 0

Question 39.
Find the inverse point of (-2, 3) with respect to the circle x² + y² – 4x – 6y + 9 = 0.
Solution:
Given equation of the circle is x² + y² – 4x – 6y + 9 = 0

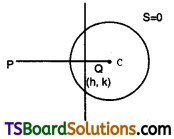
Comparing this equation with x² + y² + 2gx + 2fy + c = 0
we get, g = -2, f = -3, c = 9
Let, the given point P(x₁, y₁) = (-2, 3)
Now, the polar of P(-2, 3) w.r.t. the given circle is S₁ = 0.
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-2) + y(3) – 2(x – 2) – 3(y + 3) + 9 = 0
⇒ -2x + 3y – 2x + 4 – 3y – 9 + 9 = 0
⇒ -4x + 4 = 0
⇒ x – 1 = 0
Let Q(h, k) be the inverse point of P(-2, 3) w.r.t. the circle x² + y² – 4x – 6y + 9 = 0.
Now, Q(h, k) is the foot of the perpendicular from P(-2, 3) w.r.t. x – 1 = 0

∴ The inverse point of (-2, 3) is (1, 3).

Here students can locate TS Inter 2nd Year Physics Notes 14th Lesson Nuclei to prepare for their exam.

TS Inter 2nd Year Physics Notes 14th Lesson Nuclei

→ Nearly 99.9% of mass of atom is concentrated in a small volume called Nucleus.

→ Radius of atom is nearly 10,000 times more than radius of nucleus.

→ Volume of nucleus is nearly 10^-12 times less than volume of atom.

→ Atomic mass unit (1u): 1 /12th mass of ¹²₆C atom is taken as “atomic mass unit”.
1.u = \(\frac{1.992647 \times 10^{-26}}{12}\) = 1.660539 x 10^-27

Energy equivalent of 1u = 931.5 MeV.

→ Isotopes: The nuclei having the same atomic number (Z) but different mass number (A) are called “isotopes”. Ex: ₈O¹⁶, ₈O¹⁷, ₈O¹⁸.

→ Isobars: The nuclei having the same mass number (A) but different atomic numbers (Z) are called “isobars”. Ex: ¹⁴₆C, ¹⁴₇N

→ Isotones : The nuclei having same neutron number (N) but different atomic number (Z) are called “isotones”. Ex: ₈₀Hg¹⁹⁸, ₇₉¹⁹⁷Au.

→ Isomers : Nuclei having the same atomic number (Z) and mass number (A) but with different nuclear properties such as radio-active decay and magnetic moments are called “isomers”.
Ex: I₃₅⁸⁰ Br^m, ⁸⁰₃₅Br^g . Here ‘m’ denotes metastable state and ‘g’ denotes ground state.

→ Positive charge of nucleus is due to protons.

→ Toted charge of electrons in an atom is (- Ze) and that of protons is (+ Ze). Where Z is atomic number.

→ Neutron is a chargeless particle. Mass of neutron and mass of proton are almost equal.

→ A free neutron is unstable when it is outside the nucleus. Its mean life period is 1000 sec.

→ Inside nucleus neutron is stable.

→ Number of neutrons in an atom is (A – Z) where A is mass number and Z is “atomic number”.

→ Volume of nucleus is proportional to mass number V ∝ A (OR) \(\frac{4}{3}\)πR³ ∝ A ⇒ R = R₀A^1/3 where RQ is a constant. R₀ = 1.2 × 10^-15 m.

→ Density of nuclear matter is almost cons-tant. It is independent of mass number A.

→ Density of nuclear matter ρ_n = 2.3 × 10¹⁷ kg/m³.

→ Einstein mass .energy equation: From theory of relativity mass is treated as another form of energy. Relation between mass and energy is E = mc². Where c = Velocity of light = 3 × 10⁸ m/s.

→ In a nuclear reaction Law of conservation of energy states that the initial energy and, final energy are equal provided the energy associated with mass is also taken into account.

→ Mass defect: In every nucleus the theore-tical mass (M_T) is always less than practical mass (M). The difference of mass of nucleus and its constituents is known as “mass defect”. Mass defect Δm = [Zm_p + (A – Z) m_n] – M.

→ Binding energy : When a certain number of protons and neutrons are brought together to form a nucleus the certain amount of energy E_b is released.
The energy released while forming a nucleus is called “Binding energy E_b“. Binding energy = Δmc².
Note : We have to supply an amount of energy equals to E_b from outside to divide a nucleus into its constituents.

→ Nuclear force:

• A nuclear force is much stronger than the coulomb1 force between the charges or the gravitational force between masses.
• Nuclear force between two nucleons is distance dependent.
• From potential energy graph of a pair of nucleons these forces are found to be attractive forces when separation between nucleons is 0.8 Fermi or more. These forces are found to be repulsive forces when separation between nucleons is less than 0.8 Fermi.
• Nuclear forces are saturated forces.
• Nuclear forces does not depend on charge. So nuclear force between proton-proton, proton – neutron and neutron – neutron are equal.

→ Radioactive decay : The spontaneous disintegration of unstable nucleus is referred as “radioactivity or radioactive decay”.
When a nucleus undergoes radioactive decay three types of radioactive decay takes place.

• α – decay : In this process ₂⁴He nuclei are emitted.
• β – deay : In this process electrons or positrons are emitted.
• γ – decay : In this process high energy photons (E.M. Waves) are liberated.

→ Law of radioactive decay : Let N is the number of nuclei in a sample. The number of nuclei (ΔN) undergoing radioactive decay during the time ‘Δt’ is given by
\(\frac{\Delta \mathrm{N}}{\Delta \mathrm{t}}\) N or \(\frac{\Delta \mathrm{N}}{\Delta \mathrm{t}}\) = λN

Where λ is disintegration constant or decay constant.

→ Decay rate (R) or Activity: The total decay rate of a sample is the number of nuclei disintegrating per unit time.
∴ Total decay rate R = – \(\frac{\mathrm{dN}}{\mathrm{dt}}\) (OR)
R = R₀e^λt (or) R = λN (activity )
Total decay rate is also called activity.

→ Half – life period (T_1/2): The half-life period of a radioactive nuclide is the time taken for the number of nuclei (N) to become half of initial nuclei (N_o) i.e., N = \(\frac{\mathrm{N}_{\mathrm{o}}}{2}\).

→ Average life time : In a radioactive substance some nuclei may live for a long time and some nuclei may live for a short time. So we are using average life time T.

→ Becquerel (Bq): Becquerel is a unit to mea-sure radioactivity of a substance.
If a radioactive substance ungergoes 1 disintegration or decay per second then it is called Becquerel.

→ Curie: It is a unit to measure radioactivity of a substance.
If a radioactive substance undergoes 3.7 × 10¹⁰ decays per second then radioactivity of that substance is called curie.

Note:

• Curie is a very big unit. So generally millicurie is used to measure radioactivity,
• 1 Curie = 3.7 × 10¹⁰ Bq (Becquerel)

→ Alpha decay : In α – decay ₂He⁴ nuclie is emitted from given radioactive substance. So mass number of product nucleus (called daughter nucleus) is decreased by four units and atomic number is decreased by two units. Equation of α – decay is
^A_ZX → ^A-4_Z-2X + ⁴₂He (a-particle)

→ Average life time τ = \(\frac{\mathrm{T}}{0.693}=\frac{\text { Half }-\text { life period }}{0.693}\)

→ Power of nuclear reactor P = \(\frac{\text { Number of fission } \times \text { Energy per fission }}{\text { time }}\)
Or
P = \(\frac{n}{t}\) × E

Here students can locate TS Inter 2nd Year Physics Notes 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits to prepare for their exam.

TS Inter 2nd Year Physics Notes 15th Lesson Semiconductor Electronics: Material, Devices and Simple Circuits

→ Classification of solids (based on resistance or conductivity)

→Metals : Solids with low resistivity (ρ) or high conductivity (σ) are called metals.
Resistivity (ρ) of metals is 10^-2 – 10^-8 ohm – m.
Conductivity (σ) of metals is 10² to 10⁸ S m^-1.

→ Semiconductors: For semiconductors the resistivity (ρ) and conductivity (σ) are in intermediate range.
Resistivity (ρ) is 10^-5 to 10⁶ Ω m ;
Conductivity (σ) is 10⁵ to 10^-6 S m^-1.

→ Insulators : For insulators the resistivity (ρ) is very high and conductivity (σ) is very less.
Resistivity (ρ) is 10¹¹ to 10¹⁹ Ω m ;
Conductivity (σ) is 10^-11 to 10^-19 Sm^-1.
Note: Resistivity is not the only criteria to classify solids. Many other factors are also taken into account.

→ Semiconductors :

• In semiconductor devices the supply and flow of charge carriers are within the solid itself.
• Semiconductors are again divided into two types.
  • Elemental semiconductors : Elements such as Germanium (Ge) and Silicon (Si) are called “elemental semiconductors”
  • Compound semiconductors: These are again two types.
    • Inorganic semiconductors such as CdS, GaAs, CdSe, InP etc.
    • Organic semiconductors such as anthracene, doped pthalocyanlnes etc. and
      Organic polymers such as polypyrrole, polyaniline etc.

→ Energy Bands:

• According to Bohr theory in an isolated atom the energy of any electron is decided by the orbit in which it revolves.
• When atoms come together to form a solid these energy levels will come close together or even they may overlap. As a result an electron will have different energy levels with continuous variation of energy, which leads to the concept of energy bands.
• Valence band: The energy band which incl-udes all the energy levels of valence electrons is called “valence band”.

→ Conduction band: The energy level above valence band is called “conduction band”.
If there is some gap between valence band and conduction band then electrons in valence band will be bounded and there are no free electrons in conduction band. Note : If the lowest energy level of conduction band coincides with highest energy level of valence band or if lowest energy level of conduction band is less than highest energy level of valence band then electrons can freely go to conduction band with no external energy this is the case with most of the solids.

→ Forbidden band : The energy gap between valence band and conduction band where we cannot see any electrons is called “for-bidden band”.
Note: In case of semiconductors forbidden band width is less than 3 eV. (For Germanium it is 0.7eV and for Silicon it is 1.1 eV). Because of this small gap even at room temperatures some electrons from valence band can acquire enough energy they will cross the forbidden gap and goes to conduction band due to this reason resistance of semiconductors is less.

→ Intrinsic semiconductors: Semiconductors with ultra high pure state are called “intrinsic semiconductors”.
In pure Germanium (Ge) or Silicon(Si) crystal every Germanium or Silicon atom forms four covalent bonds with neighbouring Ge/Si crystal.
At very low temperature, intrinsic semi-conductors are insulators when temperature increases electrons absorbs more thermal energy and it may become a free electron and that atom will become positive.
A free electron leaves a positive site called hole. Le., thermal energy effectively ionises a few atoms. •
In intrinsic semiconductors number of free electrons (n^ is equal to number of holes (n^) and current contribution by electrons (7J and holes (1^) is same.
∴ In an intrinsic semiconductor n_e = n_h = n₁
Total current I = I_e + I_h

→ Extrinsic semiconductors: A suitable amount of impurity is added to intrinsic semiconductor to promote its conductivity. Such type of semiconductors are called “extrinsic semiconductors” or “impure semi-conductors”.

→ Doping: The process of deliberate addition of impurities to intrinsic semiconductor to promote conductivity is called “doping”.

→ n – type semiconductors: When pentavalent impurities such as phosphorous (P), arsenic (As), antimony (Sb) are added to intrinsic semiconductors then they are called “n-type semiconductors”.
In these semiconductors current flows through negative charges (electrons) so they are called n-type.
Note : In n-type semiconductors majority charge carriers are “electrons”, minority charge carriers are “holes”.

→ p-type semiconductors : When trivalent impurities such as Boron (B), Aluminium (Al), Galium (Ga), Indium (In) etc. are added to intrinsic semiconductor then it is called “p type semiconductor”.
In these semiconductors current flows through positive charges called holes. So they are called p-type semiconductors.
Note : In p-type semiconductors majority charge carriers are “holes” and minority charge carriers are “electrons”.

→ p-n junction : A p-n junction is formed by adding a small quantity of pentavalent impurities in a highly controlled manner to a p-type silicon/germanium wafer.

→ During the formation of p-n junction diffusion and drift of charge carriers takes place.

→ In a p-n junction concentration of holes is high at p – side and concentration of electrons is high at n-side. Due to the concentration gradient between p-type and n-type regions holes diffuse to n-region and electrons diffuse to p-region. This leads to diffusion current.

→ Due to diffusion of electron an ionised donor is developed at n-region and due to diffusion of holes to n- region an ionised acceptor will develop at p-region. These ions are immobile. So some – ve charge is developed in p-region and positive charge is developed in n-region. This space charge prevents further motion of electrons and holes near junction.

→ Depletion layer : Both the negative and positive space charge regions near junction are called “depletion region”.

→ Drift: The motion of charge carriers due to the electric field is called drift. Current flowing due to drift of charges is called “drift current*.
Note : In a p-n junction total current is the sum of diffusion current and drift current. The direction of drift current is opposite to diffusion current.

→ In a p-n junction initially diffusion current is large and drift current is small.

→ In a p-n junction under equilibrium conduction there is no net current.

→ p-n junction forward bias: When external voltage ‘V is applied to a p-n junction such thatp-region is connected to ‘+ ve’ terminal and n region is connected to ‘-ve’ terminal then it is called “forward bias”.

→ p-n junction reverse bias : When external voltage V is applied to a p-n junction such that p – region is connected to ‘- ve’ terminal and n-region is connected to ‘+ve’ terminal then it is called “reverse bias”.

→ Rectifier : The process of converting alternating current (a.c) into direct current (d.c) is called “rectification”. Instruments used for rectification is called “rectifier”.
Note : A p-n junction diode can be used as a rectifier because it allows current to flow in one direction only. i.et, in forward bias it will conduct current whereas in reverse bias it does not allow current to pass through it.

→ Zener diode : A zener diode is a highly doped p-n junction with sharp break down voltage. Generally zener is operated in reverse bias condition.
Note: In forward bias condition zener diode will also act as ordinary p-n junction.

→ Transistor : A transistor is a three layered electronic device.
These layers are called emitter, base and collector.
Transistors are two types 1) p-n-p 2) n-p-n

→ Emitter: Emitter region is of moderate size. It is heavily doped. It supplies large number of majority charge carriers for the current flow through transistor.

→ Base : Width of base region is very less. It is lightly doped nearly with 3 to 5% impurity concentration of emitter.

→ Collector: Size of collector region is larger than emitter. It is moderately doped (i.e., impurity concentration is less than emitter).

→ Biasing of transistor : In a transistor for transistor action to takes place

• Emitter base region must be forward biased,
• Base collector region must be reverse biased,
• Forward bias emitter base potential V_EB must be Jess than reverse bias collector base potential V_CB.
• If a transistor is biased as above than the transistor is said to be in active state.

→ In a transistor emitter current (I_E) = Base current (I_B) + Collector current (I_C)
I_E = I_B + I_C
Hence transistor is a current controlled device.

→ Input resistance (r₁): It is defined as the ratio of change in emitter base voltage (ΔV_BE) to change in base current (AI_g) when collector-emitter voltage is constant.
Input resistance, r_i = \(\left[\frac{\Delta \mathrm{V}_{\mathrm{BE}}}{\Delta \mathrm{I}_{\mathrm{B}}}\right]_{\mathrm{V}_{\mathrm{CE}}}\)

→ Output resistance (r₀): It is defined as the ratio of change in collector- emitter voltage (ΔV_CE) to change in collector current (I_c) when base current (I_B) is constant.
Output resistance, r₀ = \(\left[\frac{\Delta \mathrm{V}_{\mathrm{CE}}}{\Delta \mathrm{I}_{\mathrm{C}}}\right]_{\mathrm{I}_{\mathrm{B}}}\)

→ Current amplification factor (β): It is defined as the ratio of change in collector current (I_c) to change in base current (I_B) when collector – emitter voltage (V_CE) is constant.
Current amplification, β = \(\left[\frac{\Delta \mathrm{I}_{\mathrm{C}}}{\Delta \mathrm{I}_{\mathrm{B}}}\right]_{\mathrm{V}_{\mathrm{CE}}}=\frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{B}}}\)

→ Transistor as a switch : By changing the emitter base potential a transistor can be operated as a switch. For a transistor when input emitter-base potential is less than 0.6 V it is in cut off mode i.e., output current is zero. If input V_i is more than 0.6V transistor is in active state and we will get output current.
This property of output voltage V₀ is high or low is used in switches.

→ Transistor as an amplifier: A transistor can be used as an amplifier in its active region. In this region output voltage v₀ increases drastically even for a small change in input voltage V_i.
In transistor amplifier the mid point of active region is taken as operating point (also called.lnput potential) on which varying signal voltage is superposed. This vanat ion is magnified at output side by a factor equak to amplification factor β.

→ Voltage amplification factor A_v: ¡fis defined as the ratio of output signal voltage (V₀) to in put signal voltage (V_i).
Voltage amplification, A_v = \(\left[\frac{v_0}{v_i}\right]_{v_{B B}}=\beta \frac{R_C}{R_B}\)
Note : Generally voltage amplification is given at common emitter configuration VBB is emitter – base voltage in common emitter configuration.

→ Feedback amplifier : When a part of the output of an amplifier is fed as input in emitter base circuit then it is called “feed back amplifier”.
Note : Generally feedback is achieved by inductive coupling or LC or RC networks.

→ Transistor oscillator: A transistor oscillator is also a feedback amplifier with a suitable value of inductance (L) and capacitor (C) at output side. A part of output of L.C circuit is given as feedback to emitter base circuit.

Frequency of oscillation, υ = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)

→ NOT gate : It has one input terminal and one output terminal. The output of NOT gate is the opposite of input i.e., if input is ‘O’ then output is T. If input is T then output is ‘0’.

→ OR gate: It consists of two input terminals and one output terminal. In this gate if any one input terminal is high then the output is also high as shown in truth table.

→ AND gate : It consists of two input terminals and one output terminal. In AND gate if both input signals are high (say A and B) then only output is high truth table is as shown.

→ NAND gate: It consists of two input terminals and one output terminal. NAND gate is a combination of AND gate and NOT gate. If any one of input signal (A or B) is ‘O’ we will get T as output.

→ NOR gate : It consists of two input terminals and one output terminal. NOR gate is a combination of OR gate and NOT gate. The output is the negative of OR gate as shown in truth table.

Here students can locate TS Inter 2nd Year Physics Notes 16th Lesson Communication Systems to prepare for their exam.

TS Inter 2nd Year Physics Notes 16th Lesson Communication Systems

→ Communication is the act of transmission of information.

→ Electronic communication refers to faithful transfer of information or message in the form of electrical voltage or current from one point to another point.

→ World Wide Web (WWW) : Tim Berners – Lee invented the World Wide Web.
WWW may be regarded as the mammoth encyclopedia of knowledge accessible to everyone round the clock throughout the year.

→ Essentials of communication system: Every communication system has three essential elements. They are

• Transmitter
• Medium or Channel and
• Receiver.

→ In communication system transmitter and receiver are located at different places. Channel is the physical medium that connects them. Channel may consists of wires or optical fibres or even without wires called wireless transmission.

→ Purpose of transmitter is to convert the message signal produced by source into a form suitable for transmission through channel.

→ Receiver will convert the signals received through channel into a recognisable form of the original message signal.

→ Types of Communication: Communication is of two types.

• Point to point communication: Here one transmitter and one receiver are connected directly, signals can be exchanged between both of them. Ex: Telephone.
• Broadcast: In broadcast one transmitter is connected to many receivers. Here signals are unidirectional i.e., from transmitter to receiver only. Ex: Radio signals or Radio broadcasting.

→ Transducer: Any device that converts one form of energy into another form can be termed as “transducer”.
Ex : Microphone which converts sound waves into electrical signals.

→ Signal: It contains information in electrical form and suitable for transmitting through medium or channel.
Signals are two types :

• Analog signals which contains continuous variation of voltage or current.
• Digital signals con-tains two discrete states namely high (1) and low (0) out puts corresponds to 0, 1′ in binary system.

→ Noise: Noise is referred as unwanted signal present in the signal received.

→ Attenuation : The loss of strength of signal while propagating through a medium is known as “attenuation”.

→ Amplification: It is a process in which the strength of signal is increased i.e., ampli-tude of signal is increased.
Note : Amplification is necessary to com-pensate attenuation of signal in medium.

→ Range : It is defined as the maximum dis-tance between source and receiver upto which the signal can be received with sufficient strength.

→ Modulation: The process of superimposing a low frequency signal onto a high frequency carrier wave is known as “modulation”.
Note : Modulation is necessary for long range transmission of signals.

→ Demodulation: The process of recovering the superimposed signal from modulated carrier wave is called demodulation.

→ Repeater: A repeater is a combination of a receiver and transmitter. If receives signals through medium. Strength of signal is increased by amplification and again it will transmit the signals. Repeaters are highly useful to increase the range of transmission. Note : A repeater will retransmit the signals either with same carrier frequency equal to that of received signals or it may retransmit with some other carrier frequency.

→ Band width : It is the frequency difference between lowest and highest frequencies used.
Ex : Speech signals contains frequencies between 300 Hz to 3100 Hz. So band width of speech signal is 3100 – 300 = 2800.

→ Various band widths of transmission medium:

• Band width of coaxial cable is nearly 750 MHz. They are suitable for transmission upto 18 GHz frequency.
• Frequency range of transmission in optical fibre is 1 THz to 1000 THz. Band width of signals that can be transmitted is more than 100 GHz.

→ Propagation of E.M waves in space : The energy of a signal produced by transmitter is given to an antenna. Antenna will radiate the energy into space in the form of electromagnetic waves. Propagation of E.M waves in space is through different types.

→ Ground waves: For ground wave propagation attenuation on surface of earth is high. The magnitude of attenuation is proportional to frequency. Due to very high energy absorption of ground the ground wave propagation is limited to few kilometers from transmitting antenna. Range of ground wave propagation mainly depends on

• Strength or energy of transmitted signals
• Frequency of radiated signals.

→ Ionosphere: The upper part of our atmosphere is called ionosphere. At greater altitudes density of gases is less. The high energy radiation coming from sun ionizes the gas molecules in that region. Depending on ion concentration ionosphere is divided into many layers.

→ Troposphere: This region is nearly about 10 km from ground. It is formed during daytime and night-time also. It is suitable for propagation of V.H.F (Very High Frequencies).

→ D – layer: It is nearly at a height of 65 to 75 km. It is formed during daytime only. This zone will reflect L.F. signals, absorbs M.F and H.F signals to some extent.

→ E-layer: It is nearly at a height of 100 km above the earth. It is formed during day-time only. It helps for surface waves and reflects H.F waves.
Note : D-layer and E- layer zone is called stratosphere. The height of D and E layers depends on intensity of sun’s radiation.

→ Space wave: T.V. transmitting antennas are preferred to construct at elevated height such as hills or mountains and receiving antennas are placed at the top of buildings.

→ Antenna and its size: Trans miss ion of low frequency of voice signals (frequency range 20 Hz to 20,000 Hz) to longer distances is not possible because

• Energy associated with low frequency signals is less.
• For longer wavelength signals (low frequency) say voice signals of 20 kHz, the size of antenna is in the range of 15 km which is practically impossible.

Here students can locate TS Inter 2nd Year Physics Notes 8th Lesson Magnetism and Matter to prepare for their exam.

TS Inter 2nd Year Physics Notes 8th Lesson Magnetism and Matter

→ Earth behaves as a huge magnet with magnetic field pointing approximately along geographic north and south directions.

→ Every magnet has two poles namely North pole and South pole. Magnetic monopole is an imaginary concept.

→ Like poles will repel and unlike poles will attract

→ When a magnet is divided into two parts they will behave as two separate weak magnets.

→ Magnets can be made with iron and its alloys.

→ A bar magnet consists of north pole and south pole is also called magnetic dipole. Its behaviour is similar to an electric dipole of a positive and negative charge.

→ Magnetic field lines: The path followed by a free magnetic needle will represent a magnetic line of force.
Properties:

• Magnetic field lines are closed curves.
• The tangent to the field line at a given point represents the direction of net magnetic field (B) at that point.
• For a strong magnet or in a strong magnetic field these lines are denser. Around a weak magnet they are less in number.
• These lines donot intersect.

→ Bar magnet: Every bar magnet has north & south poles.

• Magnetic field lines of a bar magnet are similar to that of a solenoid of dipole moment M = NIA.
• Magnetic field for a far point on the axis of a bar magnet (B) = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{\mathrm{r}^3}\).
• On equatorial line of bar magnet
  B_E = \(\frac{\mu_0}{4 \pi}\left(\frac{M}{r^3}\right)\)
• e- For a magnetic dipole in a uniform magnetic field torque τ = m̅ x B̅ = mB sin θ.
  x = I\(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) = mB sin θ for small angles sin θ = 0.
  τ = mBθ; Time period of oscillation T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{mB}}}\)

→ Magnetic potential energy (U_m) : It is the work done by an external field to bring the magnetic poles to the given location or configuration from infinite distance.

• Magnetic potential energy U_m = -mB cos θ = m̅. B̅
• Magnetic potential energy U_m = -mB when θ = 0°.
• U_m is minimum (stable equilibrium). Magnetic potential energy Um is maximum when 0 = 180°.
• U_m maximum = mB (unstable equilibrium).

→ Gauss’s Law for magnetism : Gauss law states that the net magnetic flux through any closed surface is zero.

→ Earth’s magnetism: The magnetic field of earth is believed to arise due to electrical currents produced by convective motion of metallic fluids in outer core of earth. This effect is also known as the dynamo effect.

• The magnetic north pole of earth is at a latitude at 79.74° N and at a longitude of 71.8° W. It is some where in North Canada.
• The magnetic south pole of earth is at 79.74° S and 108.22° E in the Antarctica.

→ Magnetic declination (D) :
The magnetic meridian at a given place makes some angle (D) with true geographic north and south directions.

The angle between true geographic north to the north shown by magnetic compass is called “mag¬netic declination (or) simply declination (D).”
Note: Declination is more at poles and less at equator.

→ Angle of dip (or) inclination (I) : It is the angle of total magnetic field at a given place with the surface of earth.
Note: At a given place horizontal component of earth’s magnetic field H_E = B_E cos I.
Vertical component of earth’s magnetic field Z_E = B_E sin I.
Tangent of dip tan I = \(\frac{\mathrm{Z}_{\mathrm{E}}}{\mathrm{H}_{\mathrm{E}}}\).

→ Magnetisation (I) : It is the ratio of net magnetic moment per unit volume.
I = \(\frac{m_{\text {net }}}{V}\); Where m_net = the vectorial sum of magnetic moments of atoms in bulk material and V = volume of the given material.
Magnetic intensity is a vector, dimensions L^-1A.
Unit: Ampere/metre : A m^-1.

→ Magnetic intensity (H) : The ratio of magnetic field (B₀) to the permeability of free space (µ₀) is called “magnetic intensity”.
Magnetic intensity H = \(\frac{B_0}{\mu_0}\).

→ Solenoid, magnetic intensity and magnetic field B:
For a solenoid with the interior material of zero magnetisation material B₀ = µ₀nl. or H = \(\frac{B_0}{\mu_0}\) = nl.

→ If solenoid is filled with a material of non¬zero magnetisation material then
B = B₀ + B_m Where B_m = magnetic field due to core material. ‘
B_m = µ₀g M then H = \(\frac{\mathrm{B}}{\mu_0}\) – M

→ Magnetic susceptibility (χ) : Susceptibility is a measure for the response of magnetic materials to an external field.
χ = \(\frac{\mathrm{I}}{\mathrm{H}}=\frac{\text { Magnetic intensity }}{\text { Magnetisation }}\)
It is a dimensionless quantity.
Note : Relative permeability µ_r = 1 + χ

→ Relation between µ, µ_r and χ:
In magnetism the three quantities µ, µ_r and χ are connected with the relation
µ = µ_r(1 + χ)

→ Magnetic properties of matter : All substances are magnetically divided into three types depending on the property susceptibility (χ).
I If χ is -ve ⇒ it is dia-magnetic substance.
If χ is positive and very small ⇒ it is paramagnetic substance.
I If χ is positive and large ⇒ it is ferro-magnetic substance.

→ Diamagnetic substances:

• For these substances susceptibility x is -ve.
• In a magnetic field they will tend to travel from strong field to weak field.
• They seems to be repelled by magnets.
• For diamagnetic substances the resultant angular momentum of atoms is zero.
• Superconductors are most exotic dia-magnetic substances. For super conductors χ = -1 and µ_r = 0.
  Ex: Bismuth, Copper, Lead, Silicon etc. Note : The phenomenon of perfect diamagnetism in superconductors is called Meissner effect.

→ Paramagnetism:

• These substances are feebly attracted by magnets.
• The susceptibility (χ) of these substances is +ve and nearly equals to one.
• In a magnetic field these substances will move from weak field to strong field.
• Individual atoms posses permanent magnetic dipole moment. But due to random thermal motion of atoms net magnetic moment is zero.
• Magnetisation of paramagnetic substance is given by M = C\(\frac{B_0}{T}\) and χ = C\(\frac{\mu_0}{\mathrm{~T}}\)
  where ‘C’ = Curie constant.
  Ex : Aluminium, Sodium and Calcium etc.

→ Ferromagnetism:

• Ferromagnetic substances are strongly attracted by magnets.
• The susceptibility (χ) is +ve and very large.
• Individual atoms of these substances will spontaneously align in a common direction over a small volume called domain.
• Size of domain is nearly 1 mm³ or a domain may contain nearly 10¹¹ atoms.
• In these substances magnetic field lines are very crowded.
• Every ferromagnetic substance will transform into paramagnetic substance at a temperature called Curie Tempe¬rature (Tc).
  Ex: Manganese, Iron, Cobalt, Nickel etc.

→ Hysteresis loop : Magnetic hysteresis loop is a graph between magnetic field (B) and magnetic intensity (M) of a ferromagnetic substance.

→ Retentivity or Remanence : The magnetic intensity (H) of a material at applied magnetic field B = 0 is called retentivity. In hysteresis loop value of H on +ve Y-axis i.e., at B = 0 gives retentivity.

→ Coercivity: The -ve value of’magnetic field – (B) applied (i.e., in opposite direction of magnetisation) at which the magnetic intensity (H) inside the sample is zero is called “coercivity”. In hysteresis diagram the value of B on -ve X-axis gives coercivity.

Here students can locate TS Inter 2nd Year Physics Notes 6th Lesson Current Electricity to prepare for their exam.

TS Inter 2nd Year Physics Notes 6th Lesson Current Electricity

→ Ohm’s Law: At constant temperature current (I) flowing through a conductor is proportional to the potential difference between the ends of that conductor.
V ∝ I ⇒ V = RI where R = constant called resistance. Unit: Ohm (Ω).

→ Conductors – Resistance:
Resistance: The obstruction created by a conductor for the mobility of charges through it is known as “resistance”.

• The resistance of a conductor (R) is proportional to length; R ∝ l → (1)
• and Inversely proportional to area of cross section of the conductor.
  R ∝ l → (2)
  From eq. (1) & (2) R ∝ \(\frac{l}{\mathrm{~A}}\) ⇒ R = \(\frac{\rho l}{\mathrm{~A}}\)
  ⇒ ρ = \(\frac{\mathrm{RA}}{l}\)
  where p = resistivity of the conductor.

→ Current density (J):
The ratio of current through a conductor to its area of cross-sec¬tion is called “current density (j).”
Current density (j) = \(\frac{\text { Current }}{\text { Area }}=\frac{I}{A}\)

Note:

• Potential V = IR = I\(\frac{\rho \cdot l}{\mathrm{~A}}\) = jρl
• Potential V = E.I. (Intensity of electric field x distance)
  ∴ EI = JpI or E = jp or j = \(\frac{E}{\rho}\) = Eσ
  where σ Is conductivity of the material.

→ Drift velocity (v_d): The speed with which an electron gets drifted in a metallic conductor under the application of external electric field is called “drift velocity (v_d).”

→ Drift Velocity v_d = \(\frac{-\mathrm{eE}}{\mathrm{m}}\)τ. Where τ = the average time between two successive collisions.
Note: Current density j = \(\frac{\mathrm{ne}^2}{\mathrm{~m}}\)τE and Conductivity = σ = \(\frac{\mathrm{ne}^2}{\mathrm{~m}}\)τ.

→ Mobility (μ): It is defined as the mag-nitude of drift velocity per unit electric field.
μ = \(\frac{\left|\mathrm{v}_{\mathrm{d}}\right|}{\mathrm{E}}\) But vd = \(\frac{\mathrm{e} \mathrm{E}}{\mathrm{m}}\) ⇒ μ = \(\frac{v_d}{E}=\frac{e \tau}{m}\)

→ Resistivity: Resistivity of a substance
ρ = \(\frac{\mathrm{RA}}{\ell}\)
It is defined as the resistance of a unit cube between its opposite parallel surfaces.
Resistivity depends on the nature of substance but not on its dimensions.
Unit: Ohm – metre (Ωm).

→ Temperature coefficient of resistivity:
The resistivity of a substance changes with temperature. ρ_T = ρ₀ [l + α(T – T₀)].
Where α = temperature coefficient of resistivity.
α = \(\)/°C

Note:

• For metals a Increases with temperature.
• For semiconductors and insulators a decreases with temperature.

→ Colour code: Carbon resistors have a set of coaxial coloured rings on them. It gives the value of that resistor along with tole¬rable limit.
On every carbon resistor four colour bands are printed. In some cases only Three colour bands are printed.
1st two bands from left to right gives the numerical values of that resistor.
3rd band gives number of zero’s to be put after first two digits.
Fourth band gives maximum allowed variation limit of that resistor called “tolerance”.

→ Colour code – Values:

• Black → 0;
• Brown → 1;
• Red → 2
• Orange → 3;
• Yellow → 4
• Green → 5
• Blue → 6;
• Violet → 7;
• Gray → 8;
• White → 9

→ Tolerance: Gold band – 5 %; Silver band -10 %. If there is no 4th band tolerance is 20%. Ex: A carbon resistor consists of Orange, green, green bands then its value is
1st orange = 3. 2nd band green = 5,
3rd green = 5
No Fourth band ⇒ tolerance is 20%
So for that resistor the value is 35 followed by five zero’s.
∴ Resistance of resistor is 3500000 Q
i. e., R = 3.5 Mega ohms with 20% tolerance.

→ Electrical Power (P): Energy dissipated per unit time is “power”.
In a conductor of resistance R’ while carrying a current I, this power produces heat in that conductor.
Power P = I²R = VI = V²/R. Unit: Watt.

→ Transmission power loss (P_c): Power wasted in transmitting lines P . While supplying electrical power from generator to consumer is P_c = I²R_c => P_c = \(\frac{\mathrm{P}^2 \mathrm{R}_{\mathrm{c}}}{\mathrm{V}^2}\)
i. e., power wasted in a line is inversely proportional to the square of voltage of line. P = total power to be transmitted.
∵ P_c ∝ \(\frac{1}{\mathrm{~V}^2}\) we are prefering high voltage transmission lines to reduce transmission power losses.

→ Resistors in series: When resistances are connected in series (1) Same current flows through all resistors.
Effective resistance (R_eff) is the sum of individual resistances i.e., R_eff = R₁ + R₂ + R₃ + ……………..
ii) Effective resistance R_eff is greater than the greatest value of resistor in that combination.

→ Resistors in parallel:

• When resistors are connected in parallel potential difference across all resistors is same.
• Effective resistance is given by \(\frac{1}{R_{\text {efl }}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)
• Effective resistance is less than least resistor in that combination.

→ Cells emf and Internal resistance: emf of a cell (ε):
The open circuit voltage between negative and positive terminals of a cell is called “emf of that cell”.

→ Internal resistance of cell (r):
In a cell current flows through electrolyte. Every electrolyte has some finite resistance.
The resistance offered by the cell for the flow of current through it is called “internal resistance of the cell (r).
Note: When a cell is connected in a circuit then potential difference across terminals is V = ε – ir
Current in the circuit i = ε/(R + r)
Where E = emf of cell, r = internal resis-tance and R = resistance of the circuit.

→ Cells in series:
Let two cells of emf ε₁ and ε₂ with internal resistance r₁, and r₂ are connected in series then
i. e., power wasted in a line is inversely proportional to the square of voltage of line. P = total power to be transmitted.
∵ P_c ∝ \(\frac{1}{\mathrm{~V}^2}\) we are prefering high voltage transmission lines to reduce transmission power losses.

→ Resistors in series: When resistances are connected in series (1) Same current flows through all resistors.
Effective resistance (R_eff) is the sum of individual resistances i.e., R_eff = R₁ + R₂ + R₃ + …………
ii) Effective resistance R_eff is greater than the greatest value of resistor in that combination.

→ Resistors in parallel:

• When resistors are connected in parallel potential difference across all resistors is same.
• Effective resistance is given by
  \(\frac{1}{\mathrm{R}_{\mathrm{efl}}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)
• Effective resistance is less than least resistor in that combination.

→ Cells emf and Internal resistance : emf of a cell (ε) : The open circuit voltage between negative and positive terminals of a cell is called “emf of that cell”.

→ Internal resistance of cell (r) : In a cell current flows through electrolyte. Every electrolyte has some finite resistance.
The resistance offered by the cell for the flow of current through it is called “internal resistance of the cell (r).”
Note: When a cell is connected in a circuit then potential difference across terminals is V = ε – ir
Current in the circuit i = ε/(R + r)
Where E = emf of cell,
r = internal resistance and
R = resistance of the circuit.

→ Cells in series: Let two cells of emf ε₁ and ε₂ with internal resistance r₁, and r₂ are

• total emf ε = ε₁ + ε₂
• total p.d across them
  V = ε₁ + ε₂ – i(r₁ + r₂)
• equivalent resistance r_eq = r₁ + r₂
• current in circuit I = \(\frac{\varepsilon_1+\varepsilon_2}{R+r_1+r_2}\)
• Due to series combination potential difference in the circuit increases.

Note : If n identical cells are connected in series emf ε = nε₁, I = nI₁, r_eff = n .r .
Where ε₁ = emf of single cell,
I₁ = current given by single cell in circuit
r = internal resistance of each cell.

→ Parallel combination of cells: Let two cells of emf ε₁ and ε₂ are connected parallel then

• Equivalent emf ε_eq = \(\frac{\varepsilon_1 \mathbf{r}_2+\varepsilon_2 r_1}{r_1+r_2}\)
• Equivalent resistance \(\left(\frac{1}{r_{\mathrm{eq}}}\right)=\frac{1}{r_1}+\frac{1}{r_2}\)
  ⇒ r_eq = \(\frac{r_1 r_2}{r_1+r_2}\)
• Current in circuit I = I₁ + I₂
• P.D in circuit V = \(\frac{\varepsilon_1 r_2+\varepsilon_2 r_1}{r_1+r_2}-I\left[\frac{r_1 r_2}{r_1+r_2}\right]\)
  ⇒ V_eq = ε_eq – Ir_eq
• Due to parallel combination current in the circuit increases.

Note: When n identical batteries are connected in parallel.

• emf ε₁ = ε
• Current I = nI₁
• effective internal resistance of combination r_eff = \(\frac{r}{n}\)

→ Kirchhoff s Laws:

• Junction rule : At any junction sum of currents towards the junction is equals to sum of currents away from the junction. (OR) Algebraic sum of currents around a junction is zero.
• Loop rule : Algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.

→ Wheatstone’s principle : In a balanced Wheatstone’s bridge ratio of resistances in adjacent arms is constant.
i.e \(\frac{P}{Q}=\frac{R}{S}\Rightarrow \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\mathrm{R}_3}{\mathrm{R}_4}\)
⇒ \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l}{(100-l)}\)

→ Average current I = \(\frac{\Delta q}{\Delta t}\); Instantaneous current i = \(\frac{\mathrm{dq}}{\mathrm{dt}}\); Current density j = i/A Unit : Amp/rn2

→ Resistance R = \(\frac{V}{i}\); Resistance R = \(\frac{\rho l}{\mathrm{~A}}=\frac{\rho l}{\pi \mathrm{r}^2}\); Conductance G = \(\frac{1}{R}\).

→ AcceleratIon of electron In electric field a = \(\frac{\mathrm{eE}}{\mathrm{m}}\)

→ Drift velocity of electron (v_d) = \(\frac{i}{\text { neA }}\), V_d = \(\frac{e \tau E}{m}\); mobility (μ) = \(\frac{\mathrm{e \tau}}{\mathrm{m}}\) where τ average time between two successive collisions.

→ ResIstivity (or) specific resistance
ρ = \(\frac{\mathrm{RA}}{l}=\frac{\mathrm{R} \pi \mathrm{r}^2}{l}\); Conductance σ = \(\frac{1}{\rho}\)

→ Temperature coefficient of resistivity
α = \(\frac{\rho_2-\rho_1}{\rho_1\left(t_2-t_1\right)}\)/°C ⇒ α = \(\frac{\mathrm{d} \rho}{\rho \mathrm{dt}}\)/°C

→ Temperature coefficient of resistance
α = \(\frac{\mathrm{R}_{\mathrm{t}}-\mathrm{R}_0}{\mathrm{R}_0\left(\mathrm{t}_2-\mathrm{t}_1\right)}\)/°C
α = \(\frac{\mathrm{dR}}{\mathrm{Rdt}}\) (or) α = \(\frac{\mathrm{R}_2-\mathrm{R}_1}{\mathrm{R}_1\left(\mathrm{t}_2-\mathrm{t}_1\right)}\)/°C
R_t = R₀[1 + α(t₂ – t₁)]

→ If two wires are made of same material then
\(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{l_1}{l_2} \frac{\mathrm{A}_2}{\mathrm{~A}_1} \Rightarrow \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{l_1 \mathrm{r}_2^2}{l_2 \mathrm{r}_1^2}\)

→ In series combination of resistors:

• R_eq = R₁ + R₂ + …………. + R_n
• Same current will flow through all resistors.
• Potential drop on resistors V₁ = i R₁, V₂ = i R₂ etc.
• Total potential drop V = V₁ + V₂ + ……………. etc.
• Current of circuit I = \(\frac{\text { Total Potential }}{\text { Total Resistance }}=\frac{V}{R_{e q}}\)

→ In parallel combination of resistors:

• \(\frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}+\ldots \ldots \ldots+\frac{1}{R_n}\)
• For two resistors (R_eg) = \(\frac{\mathrm{R}_1 \mathrm{R}_2}{\mathrm{R}_1+\mathrm{R}_2}\)
• Same potential difference is applied on all resistors.
• Total current I = I₁ + I₂ + I₃ + ……… i.e., sum of individual currents through each resistor.
  I = \(\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{eq}}}=\mathrm{V}\left(\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\ldots .+\frac{1}{\mathrm{R}_{\mathrm{n}}}\right)\)

→ In cells

• While discharging, termina! voltage V = E – ir
• While charging. terminal voltage V = E + ir
• Current in circuIt i = \(\frac{E}{R+r}\)
  r = Internal resistance of battery;
  R = Resistance in circuit.

→ Electrical energy W = Vit = i²Rt = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)t

→ Electric power P = Vi = i²R = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)t; Power wasted in transmission lines P_c = P²R_c/V² where P = Power transmitted ;
R_c = Resistance of line

→ 1 kilo watt hour = 36 × 10⁵ J or 3.6 × 10⁶ J.

→ At balance condition in Wheatstone’s bridge \(\frac{P}{Q}=\frac{R}{S}\)

→ If capacitors are used in balanced Wheat stone’s bridge \(\frac{C_1}{C_2}=\frac{C_3}{C_4}\)

→ In meter bridge at balance condition \(\frac{\mathrm{R}}{\mathrm{S}}=\frac{l_1}{l_2}\)
Unknown resistance x = R\(\frac{l_1}{l_2}\)
where I₂ = (100 – I₁)

→ In potentiometer,
In comparison of emf of two cells \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2}\)

→ In determination of internal resistance
r = R\(\left[\frac{l_1-l_2}{l_2}\right]\)

Here students can locate TS Inter 2nd Year Physics Notes 5th Lesson Electrostatic Potential and Capacitance to prepare for their exam.

TS Inter 2nd Year Physics Notes 5th Lesson Electrostatic Potential and Capacitance

→ Coulomb force between two stationary charges is also a conservative force, i.e., work done in moving a test charge depends only on initial and final positions but not on the path.

→ Potential due to a point charge q’ at a distance ‘r’ V(r) = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r}\)

→ Potential due to a system of charges :
Consider a system of charges q₁, q₂, q₃, ………… q_n then potential at a point P = the algebraic sum of individual potentials at that point.
V = V₁ + V₂ + V₃ + ……….. + V_n
or
V = \(\frac{1}{4 \pi \varepsilon_0}\left(\frac{\mathrm{q}_1}{\mathrm{r}_1}+\frac{\mathrm{q}_2}{\mathrm{r}_2}+\frac{\mathrm{q}_3}{\mathrm{r}_3}+\ldots \ldots+\frac{\mathrm{q}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}}\right)\)

→ Potential on a conducting sphere :
When a charge q’ is given to a conducting sphere it will be uniformly distributed over the sphere of radius R’.
(a) Potential at a distance ‘r’
(V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\). (r > R)
(b) For a point inside the shell the potential is constant V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{R}\)

→ Equipotential surface :
An equipotential surface has a constant potential at all points on that surface.
Ex: Potential at a distance V from charge q’
(V) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\). Now a circle of radius r from q’ will have same potential i.e., that
circle represents an equipotential circle.
Note Work done in moving a charge q’ on an equipotential surface is zero.

→ Potential energy due to a system of charges:
Consider two charges say q₁ and q₂ placed at positions r₁ and r₂ from origin. Then distance between them = r₁₂.

(a) Potential energy of the system of two charges
U = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}\)

(b) If a system has three charges say q₁ q₂ and q₃ at positions r₁, r₂ and r₃ then potential energy of that system = the alzebraic sum of potential energy between every two charges.
∴ Potential energy of system U = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{r_{12}}+\frac{q_2 q_3}{r_{23}}+\frac{q_3 q_1}{r_{13}}\right]\)

→ Potential energy of a dipole in an electric field :
When an electric dipole is placed in a uniform electric field. Net force on the charges are Eq and – Eq. So resultant force is zero. But dipole will experience some torque τ on it. So it will rotate say from position θ1 to θ2 with the field (E). Torque τ = workdone by external field E
W = PE (cos θ₀ – cos θ₁) where
p = dipolemoment.

→ Electrostatic potential is constant through out the volume of the conductor and has same value equal to that on the surface.

→ Electric field at the surface of a charged a conductor E = \(\frac{\sigma}{\varepsilon_0}\)n .

→ Dielectrics : Dielectrics are the substances which does not conduct electricity.

→ Dielectric constant is defined as the ratio of force between two charges in vacuum to force between the same charges with a dielectric between them when distance is constant.
K = \(\frac{\mathrm{F}_1}{\mathrm{~F}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2} / \frac{1}{4 \pi \varepsilon} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\)
K = \(\frac{\varepsilon}{\varepsilon_0}\) = ε_r
where k = relative permittivity (or) dielectric constant.

→ Polar dielectrics: A dielectric molecule in which + ve and – ve charges are polarised into two groups without application of electric field is called polar dielectric field.

→ Non-polar dielectrics : A dielectric molecule in which the centres of all positive charges and all negative charges coincide when there is no electric field is called non polar dielectric.

→ In external electric field E’ behaviour of polar and non-polar dielectrics is same.

→ When a dielectric of constant k’ is introduced in an electric field ‘E’ then intensity of electric field inside the dielectric is reduced to E/K i.e., E_d = E/K.

→ Electric susceptibility (χ) : It is defined as the ratio of dipolemoment per unit volume to Electric field E
χ = \(\frac{P}{E}\) where P is polarisation i.e., dipole moment per unit volume.

→ Capacity (Q : It is defined as the ratio of charge Q’ to potential (V) of a conductor.
Capacity (C) = \(\frac{\text { Charge }(Q)}{\text { Potential }(V)}\) unit: Farad
Note: Capacity of a conductor depends on its geometrical shape and medium between the plates.

→ Parallel plate capacitor: It consists of two metallic plates separated by some distance ’d’ and one plate is connected to earth.
Capacity of parallel plate capacitor s0A
C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) (with vacuum between the plates)
C = K \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) (with a dielectric K filled between the plates).

→ Energy stored in a capacitor (U) : When a capacitor is charged to a potential ‘V’ it will store some electrical charge in it. While dis-charging the capacitor this electric charge is capable of doing some work. So while charging the work done to charge the capa-citor is stored in the form of potential energy in it.
Energy stored in a capacitor
U = \(\frac{1}{2}\)CV² = \(\frac{\mathrm{QV}}{2}=\frac{\mathrm{Q}^2}{2 \mathrm{C}}\)

→ Energy density (OR) Energy stored per unit volume : It is defined as the ratio of energy stored in a capacitor to the total volume between the plates of a capacitor.
Energy density U = \(\frac{1}{2}\)ε₀E²
Where E is intensity of electric field between the plates.

→ Van deGraaff generator: It is used to produce very high voltages such as 1 million volts.

→ Force between two charges in free space is
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\)

→ Relative permittivity ε_r = \(\frac{\varepsilon}{\varepsilon_0}\)
\(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ N – m²/C²
ε₀ = 8.854 × 10^-12 F/m or \(\frac{c^2}{N-m^2}\)

→ From the superposition principle, the resultant force on a given charge due to multiple charges is \(\overline{\mathrm{F}}_{\mathrm{R}}=\overline{\mathrm{F}}_1+\overline{\mathrm{F}}_2 \ldots \ldots \ldots \overline{\mathrm{F}}_{\mathrm{n}}\) (Vector sum of forces)

→ Intensity of electric field E = \(\frac{\mathrm{F}}{\mathrm{q}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}^2}\)

→ Force experienced by a charge q in electric field E is F = Eq.

→ Potential due to a point charge is V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)

→ Relation between Intensity of electric field E̅ and potential V is E = \(\frac{V}{d}\).

→ Workdone to move a charge q through a potential V is W = qV.

→ Electrostatic potential due to a system of charges is
V_R = V₁ + V₂ + V₃ + ……….. + V_n
(algebraic sum of individual potentials.)

→ Dipoles: A dipole consists of two equal and opposite charges separated by a distance 2a.

• Dipolemoment (p) = q2a = 2qa.
• Potential due to a dipole at any point
  V = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{qa} \cos \theta}{\mathrm{r}^2}=\frac{\mathrm{p} \cos \theta}{4 \pi \varepsilon_0 \mathrm{r}^2}=\frac{\overline{\mathrm{p}} \cdot \overline{\mathrm{r}}}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
  where r̅ is a unit vector along the line joining centre of dipole and given point.
• Torque on dipole in uniform electric field E is τ = p̅. E̅ = |p̅||E̅| sin θ
• Work done to rotate a dipole from angle θ₁ to θ₂ in electric field W = potential energy stored U(θ) = PE (cos θ₁ – cos θ₂)

→ Total electric flux through given area
\(\oint_E=\oint_s \bar{E} \cdot \overline{d s}=\oint_s\) E ds cos θ
From Gauss’s theorem \(\oint_E=\oint_s \bar{E} \cdot \overline{d s}\)E̅.ds̅ = \(\frac{\mathrm{q}}{\varepsilon_0}\)
Linear charge density λ = \(\frac{\mathrm{dq}}{\mathrm{dl}}\) where dq is charge on the infinitesimal length dl.

→ For an infinitely long straight charged conductor:
(a) Intensity at any perpendicular point is E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)
(b) Potential at any perpendicular point is V = \(\frac{\lambda}{2 \pi \varepsilon_0}\)log_e r + K

→ For a charged infinite plane sheet:
Intensity of electric field at a distance r from the plane is E = \(\frac{\sigma}{2 \varepsilon_0}\)

→ For a charged spherical shell : Surface charge density σ = \(\frac{\mathrm{dQ}}{\mathrm{dS}}\) or
σ = \(\frac{\text { Charge } \mathrm{q}}{\text { Surface area } \mathrm{S}}\)
(i) For points outside the shell
(a) Intensity of electric field E = \(\frac{\sigma}{s_0} \frac{\mathrm{R}^2}{\mathrm{r}^2}\)
(b) Potential V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\) + K where K is a constant of Integration.

(ii) For points on the surface of the sphere
(a) Intensity of electnc field E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{R}^2}\)
(b) Potential V = \(=\frac{1}{4 \pi \varepsilon_0} \frac{q}{R}\)

(iii) For points inside the shell
(a) Intensity of electric field E = O;
(b) Potential V = \(=\frac{1}{4 \pi \varepsilon_0} \frac{q}{R}\)

→ Capacity C = \(\frac{\text { Charge q }}{\text { Potential V }}\)
C = \(\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) =KC₀ with dielectric of constant K.

→ By placing a dielectric between the plates of a capacitor

• Intensity of electric field E_M = \(\frac{\mathrm{E}_0}{\mathrm{~K}}\)
• Capacity C = KC₀
• Potential V_M = \(\frac{\mathrm{V}_0}{\mathrm{~K}}\)

→ When a dielectric is partially introduced between the plates of a capacitor then its capacity
C = \(\frac{\varepsilon_0 A}{d-t+\frac{t}{K}}\) or C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}-t\left(1-\frac{1}{\mathrm{~K}}\right)}\)
decrease in distance = d – t\(\left(1-\frac{1}{\mathrm{~K}}\right)\) and ‘t’ is the thickness of the dielectric slab.

→ In parallel combination of capacitors, the resultant capacity C = C₁ + C₂ + C₃ + ……… etc.

→ When capacitors are connected in series, the resultant capacity is given by
\(\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)….or C = \(\frac{\mathrm{C}_1 \mathrm{C}_2}{\mathrm{C}_1+\mathrm{C}_2}\)

→ Energy stored in a capacitor
U = \(\frac{1}{2}\)CV² = \(\frac{\mathrm{Q}^2}{2 \mathrm{C}}=\frac{\mathrm{QV}}{2}\)

→ Effect of dielectric on a capacitor :
1. When charging battery is continued
(a) Potential V = V₀;
(b) Capacity C = KC₀
(c) Charge Q = KQ₀;
(d) Energy stored U = KU₀
where V₀, C₀, Q₀ and U₀ are values without dielectric.

2. When charging battery is removed from circuit
(a) Potential V = \(\frac{\mathrm{V}_0}{\mathrm{~K}}\);
(b) Capacity C = KC₀
(c) Charge on capacitor q = q₀
(d) Energy stored U = \(\frac{\mathrm{U}_0}{\mathrm{~K}}\)

Here students can locate TS Inter 2nd Year Physics Notes 4th Lesson Electric Charges and Fields to prepare for their exam.

TS Inter 2nd Year Physics Notes 4th Lesson Electric Charges and Fields

→ Electrical charges given to conductors will flow from one end to other end. Charges moving through conductors leads to flow of current.

→ Electrical charges are two types

• positive charge,
• negative charge.

→ In the process of electrification we will remove or add electrons to substances with some techniques. Substance that looses electrons will become positive substance that gains electrons will become negative.

→ Quantisation of charge: Electric charge ‘Q ’ on a substance is an integral multiple of fundamental charge of electron, i.e., Q = ne. It is called Quantisation of charge.

→ Law of conservation of charge : The total charge of an isolated system is always con-stant. i.e., charge can not be created or des-troyed. This is known as “law of conservation of charge”.

→ Charge on electron e = 1.602 × 10^-19 C it is taken as fundamental charge.

→ Coulomb’s Law:
Force attraction (or) repulsion between the charges is proportional to product of charges and inversely proportional to the square of the distance between them.
∴ From Coulomb’s law F ∝ q₁q₂ and F ∝ 1/r²
F ∝ \(\frac{q_1 q_2}{r^2}\) (OR) F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
Where \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ N-m² / C² is a constant.
ε₀ is permittivity of free space.
Its value is 8.85 × 10^-12 farad/metre.

→ Force on a given charge (q) due to multiple charges is the vector sum of all the forces acting on the given charge.
\(\overline{\mathrm{F}_{\mathrm{R}}}=\overline{\mathrm{F}}_1+\overline{\mathrm{F}}_2+\overline{\mathrm{F}}_3\) ……….
Where F₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q^q q_2}{r_1^2}\) etc
Note : To find resultant force we must use principles of vector addition i.e., parallelogram law or triangle law.

→ Electric field : Every charged particle (q) will produce an electric field everywhere in the surrounding. It is a vector. It follows inverse square law.

→ Intensity of electric field (or) electric field strength (E̅) : Intensity of electric field or electric field at a point in space is the force experienced by a unit positive charge placed at that point.
F = Eq (or) E = (F/q), SI unit: Vm^-1

→ Electric field lines of force : Electric field lines represent electric field E due to a charge ‘q’ in a pictorial manner. When E is strong field lines are move nearer or crowded. In a weak field electric field lines are less dense.

→ Electric flux (Φ): The number of electric field line passing through unit area placed normal to the field at a given point is called “electric flux”. It is a measure for the strength of electric field at that point.

→ Electric dipole: Two equal and opposite charges separated by some distance will constitute an “electric dipole”.

→ Dipole moment (p̅): The product of one of the charge in dipole and separation between the charges is defined as “dipole moment (P̅)”.
Dipole moment (p̅) = q. 2a (or) p = 2aq
It is a vector. It acts along the direction of -q to q.
Unit: coulomb – metre.

→ Dipole in a uniform electric field : Let an electric dipole is placed in an electric field of intensity E. Then F = Eq
Torque on dipole τ = p̅ x E̅
Let p̅ and E̅ are in the plane of the paper then torque τ will act perpendicularly to the plane of the paper.

→ Linear charge density (λ) :
It is defined as the ratio of charge (Q) to length of the conductor (L).
Linear charge density
λ = \(\frac{\text { Charge }}{\text { Length }} \frac{(\mathrm{Q})}{(\mathrm{L})}\)
⇒ λ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{L}}\)
Unit: Coulomb / metre.

→ Surface charge density (σ) : W
It is defined as the ratio of charge (Q) to surface area of (A) of that conductor.
Surface charge density
σ = \(\frac{\text { Charge }}{\text { Area }} \frac{(\mathrm{Q})}{(\mathrm{A})}\)
⇒ σ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{A}}\)
Unit: Coulomb / metre²

→ Volume charge density (ρ):
It is defined as the ratio of charge on the conductor ‘Q’ to volume of the conductor.
Volume charge density
ρ = \(\frac{\text { Charge }}{\text { Volume }} \frac{(Q)}{(V)}\)
⇒ ρ = \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{V}}\)
Unit: Coulomb / m³.

→ Gauss law : The total electrical flux (Φ) through a closed surface (s) is 1/ε₀ times more than the total charge (Q) enclosed by that surface.
From Gauss law (Φ) = \(\frac{1}{\varepsilon_0}\) Q

→ Important conclusions from Gauss’s law:

• Gauss law is applicable to any closed surface irrespective of its shape.
• The term Q refers to sum of all the charges inside the gaussian surface.
• A gaussian surface is that surface for which we choosed to apply gauss law.
• It is not necessary to consider any charges out side the gaussian surface to find the flux (Φ) coming out of it.
• Gauss law is very useful in the calculations to find electric field when the system (gaussian surface) has some symmetry.

→ Charge Q = ne. Where e = charge on electron = 1.6 × 10^-19 C.

→ Force between two charges F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)

→ Force between multiple charges : In a system of charges say q₁ q₂, q₃ ………. q_n.
Force on charge qj is say F₁ = F₁₂ + F₁₃ + F₁₄ ………….. F_1n
(OR) Total force on q₁ say
F₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{r_{21}^2}+\frac{q_1 q_3}{r_{13}^2}+\ldots . .+\frac{q_1 q_n}{r_{1 n}^2}\right]\)

→ Electric field due to a point charge q’ at a point r is E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}^2}\) (OR) E̅ = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}^2}\)r̅

→ Electric flux Φ = E.Δs = E Δs cos θ.
Where θ is the angle between electric field E̅ and area vector Δs .

→ Dipole moment p = q.2a. Where q is one of the charge on dipole and ‘2a’ is separation between the charges.

→ Electric field at any point on the axis of a dipole
E_axial = \(\frac{\mathrm{q}}{4 \pi \varepsilon_0} \frac{4 \mathrm{ar}}{\left[\mathrm{r}^2-\mathrm{a}^2\right]^2}=\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{pr}}{\left(\mathrm{r}^2-\mathrm{a}^2\right)^2}\)
where r > > a then E_axial = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{p}}{\mathrm{r}^3}\)
When r is the distance of given point from centre of dipole.

→ Electric field of any point on the equatorial line of a dipole.
E_eq = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{qa}}{\left[\mathrm{r}^2+\mathrm{a}^2\right]^{3 / 2}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{p}}{\left[\mathrm{r}^2+\mathrm{a}^2\right]^{3 / 2}}\)
When r >> a then E_eq = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{p}}{\mathrm{r}^3}\)
Note : E_axial and E_eq will act along the line joining the given point ’p’ and centre of dipole ‘O’.

→ Torque on a dipole when placed in a uniform electric field E is τ̅ = p̅ x E̅ = pE sin θ.
Where θ is the angle between P̅ and E̅.

→ Charge distribution on conductors:
Charge (Q) given to a conductor will uniformly spread on the entire conductor.
(a) Linear charge density λ = \(\frac{\text { Charge }}{\text { Length }} \frac{\mathrm{Q}}{\mathrm{L}}\) unit: C/m
(b) Surface charge density σ = \(\frac{\text { Charge }}{\text { Surface area }} \frac{Q}{A}\) unit / C/m²
(c) Volume charge density ρ = \(\frac{\text { Charge }}{\text { Volume }} \frac{Q}{V}\) unit: C/m³

→ Gauss’s law : The total electric flux (Φ) coming out of a closed surface is \(\frac{1}{\varepsilon_0}\) times greater than the total charge (Q) enclosed by that surface.
Φ = \(\frac{Q}{\varepsilon_0}\)

→ Electric field due to an infinitely long straight uniformly charged wire E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)n̅.
(∵ n̅ = 1) or, E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)

→ Field due to a uniformly charged infinite plane sheet is E = \(\frac{\sigma}{2 \varepsilon_0}\)n̅.
or. E = \(\frac{\sigma}{2 \varepsilon_0}\), (∵ n̅ = 1)

→ Field due to a uniformly charged thin spherical shell:
(a) At any point out side the shell is
E = \(\frac{\mathrm{Q}}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
(b) Inside the shell electric field E = 0.