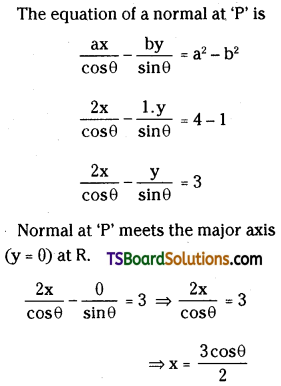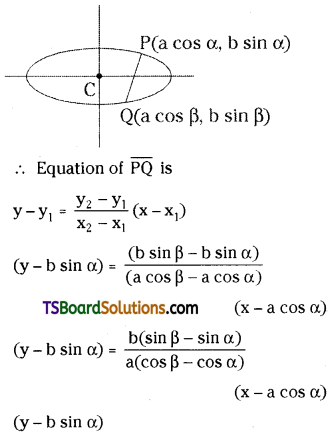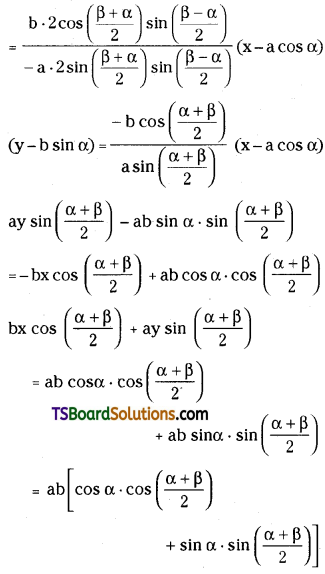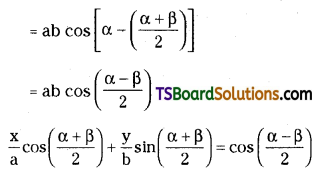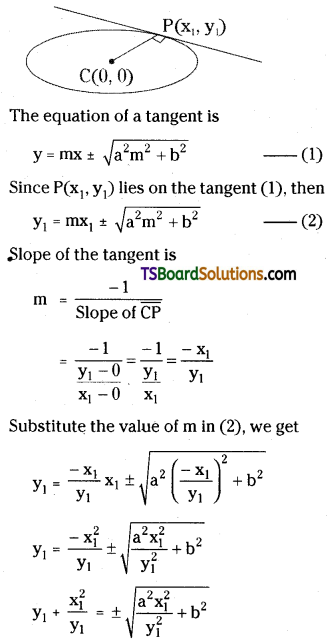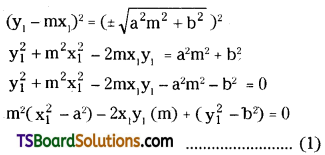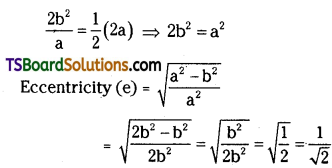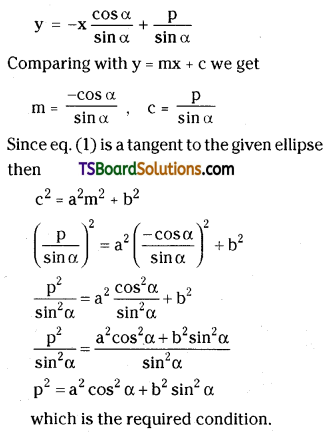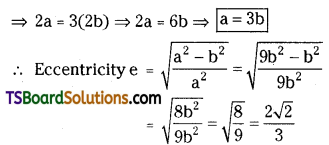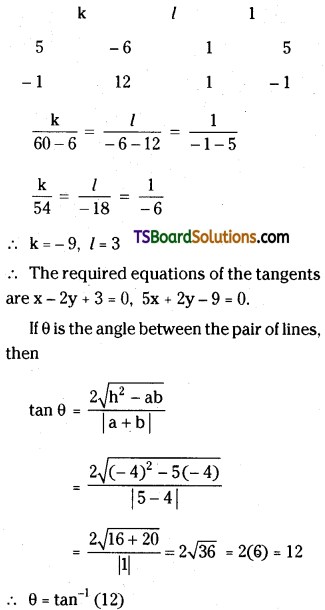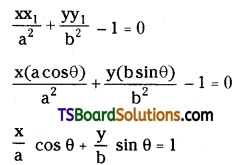Mahesh

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Hyperbola Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Hyperbola Important Questions Very Short Answer Type

Question 1.
Find the equation to the hyperbola whose foci are (4, 2) and (8, 2) and whose eccentricity is 2. (Mar. ’09)
Solution:
Given that foci are S = (4, 2), S’ = (8, 2)
eccentricity e = 2
In foci, Y-coordinates are equal then the transverse axis is parallel to X-axis.
∴ The equation of the hyperbola is of the form \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\) …….(1)
The distance between the foci is
SS’ = \(\sqrt{(4-8)^2+(2-2)^2}\) = √16 = 4
⇒ 2ae = 4
⇒ 2a(2) = 4
⇒ a = 1
Centre = Midpoint of S and S’
(h, k) = \(\left(\frac{4+8}{2}, \frac{2+2}{2}\right)=\left(\frac{12}{2}, \frac{4}{2}\right)\) = (6, 2)
∴ (h, k) = (6, 2)
We know that b² = a²(e² – 1)
⇒ b² = 1(4 – 1)
⇒ b² = 3
∴ The required equation of the hyperbola is \(\frac{(\mathrm{x}-6)^2}{1}-\frac{(\mathrm{y}-2)^2}{3}=1\)
⇒ 3(x – 6)² – (y – 2)² = 3
⇒ 3(x² + 36 – 12x) – (y² + 4 – 4y) = 3
⇒ 3x² – y² + 108 – 36x – 4 + 4y = 3
⇒ 3x² – y² – 36x + 4y + 101 = 0

Question 2.
Find the equation of the hyperbola whose foci are (±5, 0) and the transverse axis is of length 8. [(AP) May ’18, (TS) Mar. ’16]
Solution:
Given that foci = (±5, 0)
(±ae, 0) = (±5, 0)
∴ ae = 5 ……..(1)
The length of the transverse axis = 8
⇒ 2a = 8
⇒ a = 4
From (1),
4e = 5
⇒ e = \(\frac{5}{4}\)
We know that b² = a²(e² – 1)
= 16(\(\frac{25}{16}\) – 1)
= 16(\(\frac{9}{16}\))
= 9
∴ The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
⇒ 9x² – 16y² = 144

Question 3.
If 3x – 4y + k = 0 is a tangent to x² – 4y² = 5. Find the value of k. [(AP) Mar. ’20; (TS) Mar. ’18, ’17; May ’17]
Solution:
Given the equation of the hyperbola is x² – 4y² = 5
⇒ \(\frac{x^2}{5}-\frac{4 y^2}{5}=1\)
⇒ \(\frac{x^2}{5}-\frac{y^2}{5 / 4}=1\)
Here a² = 5, b² = 5/4
Given the equation of the straight line is
3x – 4y + k = 0 ………(1)
4y = 3x + k
y = \(\frac{3}{4} x+\frac{k}{4}\)
Comparing with y = mx + c, we get
m = 3/4, c = k/4
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ \(\left(\frac{k}{4}\right)^2=5\left(\frac{3}{4}\right)^2-\frac{5}{4}\)
⇒ \(\frac{k^2}{16}=5 \cdot \frac{9}{16}-\frac{5}{4}\)
⇒ \(\frac{\mathbf{k}^2}{16}=\frac{45-20}{16}\)
⇒ k² = 25
⇒ k = ±5

Question 4.
If e, e₁ is the eccentricities of a hyperbola and its conjugate hyperbola. Prove that \(\frac{1}{e^2}+\frac{1}{e_1^2}=1\). [(TS) May ’18, Mar. ’17]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
‘e’ is the eccentricity of the hyperbola then
e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)
The equation of the conjugate hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\)
‘e₁‘ is the eccentricity of the conjugate hyperbola then
e₁ = \(\sqrt{\frac{a^2+b^2}{b^2}}\)

Question 5.
If the eccentricity of a hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate hyperbola. [(AP) May ’19, ’16, ’15; (AP) Mar. ’17, ’16; (TS) Mar. ’19, ’15; (TS) May ’15; Mar. ’13; May ’13]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Given that the eccentricity of the hyperbola
e = \(\frac{5}{4}\)
The equation of the conjugate hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\)
The eccentricity of the conjugate hyperbola e’ = ?

∴ Eccentricity of the conjugate hyperbola = \(\frac{5}{3}\)

Question 6.
If the lines 3x – 4y = 12 and 3x + 4y = 12 meet on a hyperbola S = 0, then find the eccentricity of the hyperbola S = 0.
Solution:
Given equations of the lines are
3x – 4y = 12 ……….(1)
3x + 4y = 12 ………(2)
The combined equation of lines (1) and (2) is
(3x – 4y) (3x + 4y) = 144
⇒ 9×2 – 16y2 = 144
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
which represents a hyperbola of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
∴ a² = 16, b² = 9
∴ Eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)
= \(\sqrt{\frac{16+9}{16}}\)
= \(\frac{5}{4}\)

Question 7.
Find the product of lengths of the perpendiculars from any point on the hyperbola \(\frac{x^2}{16}-\frac{y^2}{9}=1\) to its asymptotes. [(TS) May ’19, ’16; (AP) Mar. ’19]
Solution:
Given equation of the hyperbola is \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
Here a² = 16, b² = 9
The product of the ⊥ar distances from any point on a hyperbola to its asymptotes = \(\frac{a^2 b^2}{a^2+b^2}\)
= \(\frac{16 \cdot 9}{16+9}\)
= \(\frac{144}{25}\)

Question 8.
Show that the Angle between the two asymptotes of a hyperbola \(\frac{\mathbf{x}^2}{\mathbf{a}^2}-\frac{\mathbf{y}^2}{b^2}=1\) is 2tan^-1(\(\frac{b}{a}\)) or 2 sec^-1(e).
Solution:
Let the equation of hyperbola be \(\frac{\mathbf{x}^2}{\mathbf{a}^2}-\frac{\mathbf{y}^2}{b^2}=1\)
The asymptotes of hyperbola are
y = ±\(\frac{b}{a}\)x where m₁ = \(\frac{b}{a}\) and m₂ = \(-\frac{b}{a}\).
If θ is the angle between asymptotes of the hyperbola then

Question 9.
If the angle between asymptotes is 30° then find its eccentricity. [(TS) Mar. ’20; (AP) May ’17; ’14]
Solution:
The angle between asymptotes of the hyperbola

Question 10.
Define rectangular hyperbola and find its eccentricity. [(AP) Mar. ’15, ’14]
Solution:
Rectangular Hyperbola: If in a hyperbola the length of the transverse axis (2a) is equal to the length of the conjugate axis (2b), the hyperbola is called a rectangular hyperbola.
Its equation is x² – y² = a² [∵ a = b]
In this case
e² = \(\frac{a^2+b^2}{a^2}=\frac{2 a^2}{a^2}=2\)
⇒ e = √2
∴ The eccentricity of a rectangular hyperbola is √2.

Question 11.
Find the equation of normal at \(\theta=\frac{\pi}{3}\) to the hyperbola 3x² – 4y² = 12.
Solution:
The given equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
The equation of normal at P(a sec θ, b tan θ) to the hyperbola S = 0 is

Question 12.
Find the equation of the hyperbola whose asymptotes are 3x = ±5y and the vertices (±5, 0).
Solution:
The asymptote equation is given by 3x – 5y = 0 and 3x + 5y = 0.
∴ The equation of hyperbola is of the form (3x – 5y) (3x + 5y) = k
⇒ 9x² – 25y² = k
If the hyperbola passes through the vertex (±5, 0) then
9(25) = k
⇒ k = 225
Hence the equation of asymptotes of a hyperbola is 9x² – 25y² = 225

Question 13.
Prove that the equations of the asymptotes of the hyperbola S = 0 are \(\frac{x}{a} \pm \frac{y}{b}=0\).
Solution:
Let the equation of the hyperbola is
S = \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\) ……..(1)
The equation of the tangent at ‘m’ is
y = mx + \(\sqrt{a^2 m^2-b^2}\) …….(2)
The point of contact of (1) & (2) is
\(\left(\frac{-a^2 m}{\sqrt{a^2 m^2-b^2}}, \frac{-b^2}{\sqrt{a^2 m^2-b^2}}\right)\)
If (2) is an asymptote, then it touches the hyperbola at infinity
Hence a²m² – b² = 0
⇒ m = ±\(\frac{b}{a}\)
∴ The asymptotes are y = ±\(\frac{b}{a}\)x
⇒ \(\frac{x}{a} \pm \frac{y}{b}=0\)

Question 14.
Find the eccentricity and length of the latus rectum of the hyperbola 4x² – 9y² = 27. (Mar. ’06)
Solution:
Given the equation of the hyperbola is 4x² – 9y² = 27

Question 15.
Find the foci of the hyperbola 9x² – 16y² + 72x – 32y – 16 = 0. (May ’01)
Solution:
Given equation of the hyperbola is 9x² – 16y² + 72x – 32y – 16 = 0
⇒ 9(x² + 8x) – 16(y² + 2y) = 16
⇒ 9(x² + 8x + 16) – 16(y² + 2y + 1) = 16 + 144 – 16
⇒ 9(x + 4)² – 16(y + 1)² = 144

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 7 Partial Fractions will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Partial Fractions Formulas

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 8 Measures of Dispersion will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Measures of Dispersion Formulas

→ Measures of Dispersion : Range, mean deviation, variance, standard deviation are some measures of dispersion.

→ Range is defined as the difference of maximum value and the minimum value of the data.

→ Mean Deviation for ungrouped distribution :

• Mean Deviation about the mean = \(\frac{1}{n}\)Σ|x_i – x̄|
• Mean Deviation about median = \(\frac{1}{n}\)Σ|x_i – Median|

→ Mean Deviation for grouped data :

• Mean Deviation about mean = \(\frac{1}{n}\)Σf_i|x_i – x̄|, where N = Σf_i
• Mean Deviation about median = \(\frac{1}{n}\)Σf_i|x_i – Median|, where N = Σf_i

→ Variance and Standard Deviation for ungrouped data
σ² = \(\frac{1}{n}\)Σ(x_i – x̄)², σ = \(\sqrt{\frac{1}{n} \Sigma\left(x_i-\bar{x}\right)^2}\)

→ Variance and Standard Deviation of a discrete frequency distribution
σ² = \(\frac{1}{N}\)Σf_i(x_i – x̄)², σ = \(\sqrt{\frac{1}{N} \Sigma f_i\left(x_i-\bar{x}\right)^2}\)

→ Standard deviation of a continuous frequency distribution
σ = \(\frac{1}{N} \sqrt{N \Sigma f_i x_i^2-\left(\Sigma f_i x_i\right)^2}\)
or
σ = \(\frac{h}{N} \sqrt{N \Sigma f_i y_i^2-\left(\Sigma f_i y_i\right)^2}\), where y_i = \(\frac{\left(x_i-A\right)}{h}\)

→ Coefficient of variation = \(\frac{σ}{x̄}\) × 100; x̄ ≠ 0.

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 9 Probability will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Probability Formulas

→ An experiment that can be repeated any number of times under essentially identical conditions in which

• All possible outcomes of the experiment are known in advance.
• The actual outcome in a particular case is not known in advance, is called a “Random experiment”,

E.g :

• In tossing an unbiased coin, we have only two possible outcomes: Head (H) and Tail (T). We can find the outcome in only one particular trial and the experiment can be done any number of times under essentially identical conditions.
• Rolling a die; denoting six faces of a cubical die with the numbers 1, 2, 3. 4. 5 and 6, the possible outcome of the experiment is one of the numbers 1, 2, 3, 4, 5 or 6.

→ Any possible outcome of a random is called an “Elementary event” or “Simple event” denoted by ’E’.

• The set of all elementary events of a random experiment is called the sample space S associated with the event ’E’.
• An elementary event is a point of the sample space S.
• A subset E of S is called an event. That is a set of elementary events is called an event.
• The complement of the event E denoted by E^c is the event given by E^c = S – E which is called the complementary event of E.
• The set Φ and the set S are trivial subsets of S are events called impossible event and certain event.

→ Events E₁ E₂, ……………… E_n are said to be mutually exclusive if E_i ∩ E_j = Φ for i ≠ j, 1 ≤ i, j ≤ n.

→ Events E₁ E₂, ……………… E_n are said to be equally likely if there is no reason to expect one of them to happen in performance to the other.

→ Events E₁ E₂, ……………… E_n are called exhaustive events if E₁ ∪ E₂ ∪ ……………… ∪ E_n = S.

→ Classical definition of Probability : If a random experiment results in n exhaustive, mutually exclusive and equally likely ways and m out of them are favourable to the happening of an event E, then the probability of E denoted by P(E) = \(\frac{m}{n}\)
For any E, 0 ≤ P( E ) ≤ 1.

→ Relative frequency definition of Probability : Suppose E is an event of a random experiment. Let the experiment be repeated n times out of which E occurs m limes. Then the ratio \(\frac{m}{n}\) is called the nth relative frequency of the event E. If a real number ‘l’ such that \({Lim}_{n \rightarrow \infty}\) rⁿ = l then l is called the Probability of E.

→ Kolmogorov’s Axiomatic definition of Probability :
Suppose S is the sample space of the random experiment and S is finite. Tiien a function P : P(S) → R satisfying the following axioms is called the Probability function.

• P(E) ≥ 0 ∀ E ∈ P( S )
• P(S) = 1
• If E₁, E₂ ∈ P( S ); then P( E ) is called the Probability of E. If S is countable of infinite then the (iii) axiom is \(P\left(\bigcup_{n=1}^{\infty} E_n\right)=\sum_{n=1}^{\infty} P\left(E_n\right)\)

→ P(Φ) = 0 and P(S ) = 1.

→ Addition theorem on Probability : If E₁ and E₂ be any two events of a random experiment, then
P(E₁ ∪ E₂) = P(E₁) – P( E₂) – P(E₁ ∩ E₂)

→ Conditional Probability of the occurrence of an event A, given that B has already happened is denoted by P(\(\frac{A}{B}\)) and is defined as P\(\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}\), P(B) ≠ 0

→ Multiplication theorem on Probability: If A and B are events of a sample space S and P (A) > 0, P (B) > 0 then P (A ∩ B) = P(A). P(\(\frac{B}{A}\)) = P (B) . P(\(\frac{A}{B}\))

→ Independent events: Events A and B of a sample space S are said to be independent if P(A ∩ B) = P(A) – P(B) otherwise they are said to be dependent.

→ Baye’s theorem : If E₁, E₂, ………….. E_n are mutually exclusive and exhaustive events of a
random experiment with P(E_i) > 0 for i = 1, 2, …………………. n then
\(P\left(\frac{E_k}{A}\right)=\frac{P\left(E_k\right) \cdot P\left(\frac{A}{E_k}\right)}{\sum_{i=1}^n P\left(E_i\right) P\left(\frac{A}{E_i}\right)}\), k = 1, 2, …….. n

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 10 Random Variables and Probability Distributions will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Random Variables and Probability Distributions Formulas

→ Bemoullian trial : If we conduct an experiment with two possible outcomes, then it is t called a Bernoullian trial.

→ Random variable : If S is the sample space of random experiment then a function X : S → R is called a random variable.

→ Discrete random variable : A random variable X whose range is either finite or countably infinite is called a discrete random variable. X is a random variable if the range of X is either { x₁, x₂, ……….. x_n} or {x₁, x₂,……. x_n}. Otherwise X is said to be a continuous random variable.

→ Probability function induced by a random variable :
Suppose S is the sample space of a random experiment. Let P : P (S) → R be a probability function and X : S → R be a random variable.
Then p’ : P (R) → R defined by p’ (Y) = P(X^-1(Y)) for each Y ∈ P (R) is a probability function induced by X.

→ Probability distribution function : Suppose X is a random variable. Then F : R → R given by F(x) = P(X ≤ x) = P[(X^-1) (-∞, x) ] for each x ∈ R is called the probability distribution function of X.

→ The probability distribution of a discrete random variable is given by

where P_i ≥ 0 for i = 1, 2, …………. and \(\sum_{i=1}\)P₁ = 1

→ The mean (μ) and variance (σ²) of a discrete random variable X are μ = Σx_n P (X = x_n) and σ² = Σ (x_n – μ)² P ( X = x_n)
= Σx_n P( X – x_n) – μ²
The standard deviation o is the square root of the variance.

→ If p is the probability of a success, q be the probability of a failure such that p + q = 1 and n is the number of Bernoullian trials, then the probability distribution of a discrete random variable X is called a binomial variate given by P(X = k) = ⁿC_k p^k q^n-k, k = 0, 1, 2, ……. n called the binomial distribution.
Here n and p are the parameters and X – B ( n, p).

→ If X – B ( n, p ) then the mean of the distribution p = np and variance of the distribution σ² = npq. The standard deviation of this distribution is \(\sqrt{n p q}\).

→ The probability distribution of a discrete random variable X (called the Poisson variable) given by P(X = k) = \(\frac{\mathrm{e}^{-\lambda} \lambda^{\mathrm{k}}}{\mathrm{k} !}\) (where k = 0,1,2,…. and λ > 0) called the Poisson distribution.
Here λ Is the parameter of X.

→ If X is a Poisson variate with parameter λ then the mean μ = variance σ² = λ.

→ Poisson distribution can be approximated as a limiting case of binomial distribution under the conditions.

• the number of trials must be very large, i.e., n → ∞
• ‘p’ the constant probability of success in each trial is very very small i.e., p → 0.
• n. p = λ, a finite positive real number.

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 5 Permutations and Combinations will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Permutations and Combinations Formulas

→ Fundamental principle: If a work W₁, can be performed in m different ways and another work W₂ can be performed in n different ways, then the two works simultaneously can be performed in mn different ways.

→ If n is a positive integer, then n! = n {(n – 1)!} and 1! = 1.

→ We define 0! 1.

→ The number of permutations of n dissimilar things taken ‘r’ at a time is denoted by
ⁿP_r and ⁿp_r = \(\frac{n !}{(n-r) !}\) for 0 ≤ r ≤ n

→ If n, r are positive integers and r ≤ n, then

• ⁿP_r = n. ^(n-1)P_(r-1) (if r > 1)
• ⁿP_r = n.(n – 1)^(n-2)P_(r-2).(if r ≥ 2).

→ The number of permutations of n dissimilar things taken V at a time

• containing a particular thing is r.^(n-1)P_(r-1)
• not containing a particular thing is ^(n-1)P_r
• containing a particular thing in a particular place is ^(n-1)P_(r-1)

→ If n, r are positive integers and r < n, then ⁿP_r = ^(n-1)P_r + r.^(n-1)P_(r-1)

→ The sum of the r-digit numbers that can be formed using the given n’ distinct non-zero digits
(r ≤ n ≤ 9) is ^(n-1)P_(r-1) × (sum of all n digits) × (111…………….1)_(rtimes)

→ In the above, if ‘0’ is one among the given ‘n’ digits, then the sum is
^(n-1)P_(r-1) × (sum of the digits) × (111……………1)_(rtimes)
^(n-1)P_(r-1) × (sum of the digits) × (111………………1)_(r-1)times)

→ The number of permutations of n dissimilar things taken r’ at a time when repetitions are allowed (i.e., each thing can be used any number of times) is n^r.

→ The number of circular permutations of n dissimilar things is (n – 1) !.

→ In the case of hanging type circular permutations like garlands of flowers, chains of beads etc., the number of circular permutations of n things is \(\frac{1}{2}\) [(n – 1) !].

→ If in the given n things, p like things are of one kind, q alike things are of the second kind, r alike things are of the third kind and the rest are dissimilar, then the number of permutations (of these n things) is \(\frac{\mathrm{n} !}{(\mathrm{p} !)(\mathrm{q} !)(\mathrm{r} !)}\)

→ The number of combinations of n things taken ‘r’ at a time is denoted by ⁿC_r and ⁿC_r = \(\frac{n !}{(n-r) ! r !}\) for 0 ≤ r ≤ n

→ If n, r are integers and 0 ≤ r ≤ n, then ⁿC_r = ⁿC_(n-r)

→ ⁿC₀ = ⁿC_n; ⁿC₁ = ⁿC_(n-1)

→ The number of ways of dividing ‘m + n’ things (m ≠ n) into two groups containing m, n things is \(\frac{(m+n+p) !}{(m !)(n !)(p !)}\)

→ The number of ways if distributing mn things equally to m persons is \(\frac{(\mathrm{mn}) !}{(\mathrm{n} !)^{\mathrm{m}}}\)

→ If p alike things are of one kind, q alike things are of the second kind and r alike things are of the third kind, then the number of ways of selecting one or more things out of them is (p + 1) (q + 1) (r + 1) – 1.

→ If m is a positive integer and m = P₁^α₁, P₂^α₂ …………. P_k^α_k where p₁, p₂, ………….. , p_k are distinct primes and α₁, α₂, …………….. α_k are positive integers then the number of divisors of m is (α₁ + 1) (α₂ + 1) ………. (α_k + 1) (This includes 1 and m).

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 4 Theory of Equations will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Theory of Equations Formulas

→ If n is a non-negative integer and a₀, a₁, a₂ ……………. a_n are real or complex numbers and a₀ ≠ 0, then the expression f(x) = a₀xⁿ + a₁x^n-1 + a₀x^n-2 + …………. + a_n is called a polynomial in x of degree n.

→ If f(x) is a polynomial of degree n > 0, then the equation f(x) = 0 is called an algebraic equation or polynomial equation of degree n.

→ A complex number a. is said to be zero of a polynomial f(x) or a root of the equation f(x) = 0, if f(α) = 0.

→ Every non-constant polynomial equation has atleast one root.

→ Relation between the roots and the coefficients of an equation:
(i) If α₁, α₂, α₃ are the roots of x³ + p₁x² + p₂x + p₃ = 0

• s₁ = α₁ + α₂ + α₃ = -p₁
• s₂ = α₁α₂ + α₂α₃ + α₃α₁ = p₂
• s₃ = α₁α₂α₃ = -p₃

(ii) If α₁, α₂, α₃, α₄ are the roots of x4 + p,x‘4 + p.,x“ + p.,x + p4 = 0, then

• s₁ = α₁ + α₂ + α₃ + α₄ = -p₁
• s₂ = α₁α₂ + α₂α₃ + α₃α₄ + α₁α₃ + α₂α₄ = p₂
• s₃ = α₁α₂α₃ + α₂α₃α₄ + α₃α₄α₁ + α₁α₂α₄ = -p₃
• s₄ = α₁α₂α₃α₄ = p₄

→ For a cubic equation, when the roots are

• in A.P., then they are taken as a – d, a, a + d.
• in G.P., then they are taken as \(\frac{a}{d}\), a, ad.
• in H.P., then they are taken as \(\frac{1}{a-d}, \frac{1}{a}, \frac{1}{a+d}\)

→ For a biquadratic equation, if the roots are

• in A.P.. then they are taken as a – 3d, a – d. a + d, a + 3d.
• in G.P., then they are taken as \(\frac{a}{d^3}, \frac{a}{d}\),ad, ad³.
• in H.P., then they are taken as \(\frac{1}{a-3 d}, \frac{1}{a-d}, \frac{1}{a+d}, \frac{1}{a+3 d}\)

→ To find a root of f(x) = 0. we have to find out a value of x, for which f(x) = 0. Sometimes we can do this inspection. This method is known as trial and error method.

• For a polynomial equation with rational coefficients, irrational roots occur in pairs,
• For a polynomial equation with real coefficients, complex roots occur in pairs.

→ If α₁, α₂,. …………………….., α_n are the roots of the equation f(x) = 0, then α₁ – h, α₂ – h, ……………. , α_n – h are the roots of the equation f(x + h) = 0 and α₁ + h, α₂ + h, ………………. , α_n + h are the roots of the equation f(x – h) = 0.

→ If f(x) = a₀xⁿ + a₁x^n-1 + ………….. + aα_n = 0, then the transformed equation whose roots are the reciprocals of the roots of f(x) = 0 is Φ(x) = a₀ + a₁x + a₂x² + + a_nxⁿ = 0.

→ If an equation is unaltered by changing x into \(\frac{1}{n}\), then it is a reciprocal equation.

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 3 Quadratic Expressions will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Quadratic Expressions Formulas

→ A polynomial of the form f(x) = ax² + bx + c (a ≠ 0) is called a quadratic expression.

→ Any equation of the form ax² + bx + c = 0 (a ≠ 0) is called a quadratic equation.

→ Let the roots of the quadratic equation ax² + bx + c = 0 be α, β then
α = \(\frac{-b+\sqrt{b^2-4 a c}}{2 a}\); β = \(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\)
Now b² – 4ac > 0 roots are real and distinct.

• b² – 4ac = 0 roots are equai and real,
• b² – 4ac < 0 roots are imaginary.
• α + β = \(\frac{-b}{a}\): αβ = \(\frac{c}{a}\)

→ Let a, b, c be rational numbers, α, β are roots of the equation ax² + bx + c = 0 then

• α, β are equal rational numbers if Δ = 0.
• α, β are distinct rational numbers if Δ is the square of a non-zero rational number.
• α, β are conjugate surds if Δ > 0 and Δ is not the square of a rational number.

→ Let f(x) = ax² + bx + c = 0, a ≠ 0, α, β are roots of equation

• if c ≠ 0 then αβ ≠ 0 and f(\(\frac{1}{x}\)) = 0 is an equation whose roots are \(\frac{1}{α}\) and \(\frac{1}{β}\)
• f(x – k) = 0 is an equation whose roots are α + k and β + k.
• f(- x) = 0 is an equation whose roots are – α and – β.

→ If α and β are roots of the equation ax² + bx + c = 0 with α < β then

• for α < x < β, ax² + bx + c and a have opposite signs.
• for x < α or x > β, ax² + bx + c and a have the same sign.

→ If a < 0, the expression ax² + bx + c has maximum at x = \(\frac{-\mathrm{b}}{2 \mathrm{a}}\) and the maximum value is given by \(\frac{4 a c-b^2}{4 a}\)

→ If a > 0, the expression ax² + bx + c has minimum at x = \(\frac{-\mathrm{b}}{2 \mathrm{a}}\) and the minimum value is given by \(\frac{4 a c-b^2}{4 a}\)

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 2 De Moivre’s Theorem will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A De Moivre’s Theorem Formulas

→ cos θ + i sin θ = e^iθ

→ cos θ – i sin θ = e^-iθ

→ (cos θ + i sin θ)ⁿ = cos nθ + isin nθ = e^iθ
If n is an integer (De Moivre’s theorem for integral index)

→ n is a rational number then (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ

→ If z₀ = r₀(cos θ + isin θ), then nth roots of z₀ = zⁿ.

→ The n^th root of unity
zⁿ = 1
z = (1)^1/n
nth roots of unity are cis \(\frac{2 \mathrm{k} \pi}{\mathrm{n}}\). k = 0, 1, 2………………..(n – 1)

→ Cube roots of unitv:
1, ω, ω²
ω = \(\frac{-1+\mathrm{i} \sqrt{3}}{2}\), ω² = \(\frac{-1-\mathrm{i} \sqrt{3}}{2}\)
1 + ω + ω² = 0
ω³ = 1

→ Fourth roots of unity:
z⁴ = 1 or z = (1)^1/4
z = 1, -1, +i, -i

Learning these TS Inter 2nd Year Maths 2A Formulas Chapter 1 Complex Numbers will help students to solve mathematical problems quickly.

TS Inter 2nd Year Maths 2A Complex Numbers Formulas

→ A complex number is an ordered pair of real numbers. It is denoted by (a, b); a ∈ R, b ∈ R.
z = a + ib
Re(z) = a ; Im(z) = b

→ Two complex numbers z₁ = a + ib and z₂ = c + id are said to be equal if a = c, b = d.

→ Algebra of complex numbers
(a) z = z₁ + z₂ = (a + c) + i (b + d)
(b) z = z₁ – z₂ = (a – c) + i (b – d)
(c) z = z₁/z₂ = \(\frac{a c+b d}{c^2+d^2}+\frac{i(b c-a d)}{c^2+d^2}\)
(d) z = z₁ . z₂ = (ac – bd) + i (ad + be)

→ If z = a + ib, then conjugate of complex number is z̅ = a – ib
z . z̅ = a² + b²

→ If z = a + ib, then modulus of z is represented by |z| = \(\sqrt{a^2+b^2}\)

→ Any real number θ satisfy the equation x = r cos θ; y = r sin θ.

→ Arg z = tan^-1\(\frac{{Im}(z)}{{Re}(z)}\) = tan^-1\(\frac{y}{x}\), -π < Arg z < π
(a) Arg (z₁. z₂) = Arg z₁ + Arg z₂+ nπ for some π ∈ {-1,0,1}.
(b) Arg (z₁/z₂) = Arg z₁ – Arg z₂ + nπ, π ∈ (-1,0,1}.

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Ellipse Important Questions to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Ellipse Important Questions

Question 1.
Find the equation of the ellipse with focus at (1, -1), e = \(\frac{2}{3}\) and directrix as x + y + 2 = 0. [(TS) Mar. ’19; (AP) May ’16]
Solution:

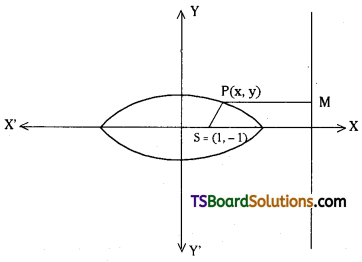
Given that focus S = (1, -1)
Equation of the directrix is x + y + 2 = 0
Eccentricity, e = \(\frac{2}{3}\)
Let P(x, y) be any point on the ellipse.
Since ‘P’ lies on the ellipse then

⇒ 9x² + 9y² – 18x + 18y + 18 – 2x² – 2y² – 4xy – 8x – 8y – 8 = 0
⇒ 7x² – 4xy + 7y² – 26x + 10y + 10 = 0
∴ The equation of the ellipse is 7x² + 7y² – 4xy – 26x + 10y + 10 = 0

Question 2.
Find the equation of the ellipse in the standard form such that the distance between the foci is 8 and the distance between the directrices is 32. [(AP) May ’17]
Solution:
Let the equation of the ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (a > b) ………(1)
Given that the distance between the foci = 8
2ae = 8
ae = 4 ……(2)
The distance between directrices = 32
\(\frac{2a}{e}\) = 32
\(\frac{a}{e}\) = 16 ……….(3)
Now (2) × (3)
ae . \(\frac{a}{e}\) = 4 . 16
⇒ a² = 64
⇒ a = 8
We know that b² = a²(1 – e²)
⇒ b² = a² – a²e²
⇒ b² = (8)² – (4)²
⇒ b² = 64 – 16
⇒ b² = 48
∴ The equation of the ellipse is \(\frac{x^2}{64}+\frac{y^2}{48}=1\)

Question 3.
Find the equation of the ellipse in the standard form whose distance between foci is ‘2’ and the length of the latus rectum is \(\frac{15}{2}\). [(AP) Mar. ’18; (TS) ’15]
Solution:
Let the equation of the ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b) ……..(1)
Given that distance between foci = 2
⇒ 2ae = 2
⇒ ae = 1
Length of latus rectum = \(\frac{15}{2}\)
∴ \(\frac{2 b^2}{a}=\frac{15}{2}\)
b² = \(\frac{15a}{4}\)
We know that b² = a²(1 – e²)
⇒ b² = a² – a²e²
⇒ \(\frac{15a}{4}\) = a² – (1)
⇒ 15a = 4a² – 4
⇒ 4a² – 15a – 4 = 0
⇒ 4a² – 16a + a – 4 = 0
⇒ 4a(a – 4) + 1(a – 4) = 0
⇒ (a – 4) (4a + 1) = 0
⇒ a = 4, a = \(\frac{-1}{4}\)
Since ‘a’ is always positive then a = 4
If a = 4, then b² = \(\frac{15(4)}{4}\) = 15
∴ The equation of the ellipse is \(\frac{x^2}{16}+\frac{y^2}{15}=1\)

Question 4.
Find the equation of the ellipse referred to its major and minor axes as the coordinate axes X, Y respectively with latus rectum of length 4, and distance between foci 4√2. [May & Mar. ’19 (AP); Mar. ’18 (TS)]
Solution:
Let the equation of ellipse be
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
by given data length of the latus rectum is
\(\frac{2 \mathrm{~b}^2}{\mathrm{a}}\) = 4
⇒ b² = 2a ……..(1)
distance between foci is
2ae = 4√2
⇒ ae = 2√2
⇒ a²e² = 8 …….(2)
Now (1) ⇒ a²(1 – e²) = 2a
⇒ a² – a²e² = 2a
⇒ a² – 8 = 2a
⇒ a² – 2a – 8 = 0
⇒ a² – 4a + 2a – 8 = 0
⇒ a(a – 4) + 2(a – 4) = 0
⇒ (a – 4) (a + 2) = 0
⇒ a = -2, 4
Since a ≠ -2 ⇒ a = 4 and
b² = 2a = 2(4) = 8
∴ Required ellipse be \(\frac{x^2}{16}+\frac{y^2}{8}=1\)

Question 5.
Find the length of the major axis, minor axis, latus rectum, eccentricity, coordinates of centre, foci, and the equations of directrices of the ellipse 9x² + 16y² = 144. [(TS) Mar. ’20, ’16; May ’19, ’17; (AP) Mar. ’17, ’15, ’14]
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Comparing with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
we get a = 4, b = 3 (a > b)
The length of the major axis = 2a = 2(4) = 8
The length of the minor axis = 2b = 2(3) = 6

Question 6.
Find the radius of the circle passing through the foci of an ellipse 9x² + 16y² = 144 and having the least radius.
Solution:
Given ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Here a² = 16 ⇒ a = 4
b² = 9 ⇒ b = 3
Eccentricity e = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{16-9}{16}}=\frac{\sqrt{7}}{4}\)
SS’ = Diameter of the circle = 2ae
⇒ Diameter of the circle = 2√7
⇒ 2r = 2√7
⇒ r = √7
i.e., Radius of the circle CS = √7

Question 7.
The distance of a point on the ellipse x² + 3y² = 6 from its centre is equal to 2. Find the eccentric angles.
Solution:
Given the equation of the ellipse is x² + 3y² = 6
⇒ \(\frac{x^2}{6}+\frac{3 y^2}{6}=1\)
⇒ \(\frac{x^2}{6}+\frac{y^2}{2}=1\)
a = √6, b = √2, a > b

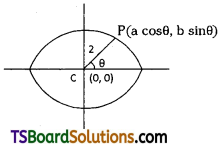
Let P(a cos θ, b sin θ) = (√6 cos θ, √2 sin θ] be a point on the ellipse.
Centre C = (0, 0)
Given that CP = 2
⇒ CP² = 4
⇒ (√6 cos θ)² +(√2 sin θ)² = 4
⇒ 6 cos²θ + 2 sin²θ = 4
⇒ 4 cos²θ + 2 cos²θ + 2 sin²θ = 4
⇒ 4 cos²θ + 2(cos²θ + sin²θ) = 4
⇒ 4 cos²θ + 2 = 4
⇒ 4cos²θ = 2
⇒ cos²θ = \(\frac{1}{2}\)
⇒ cos θ = \(\pm \frac{1}{\sqrt{2}}\)
If cos θ = \(\frac{1}{\sqrt{2}}\) ⇒ θ = \(\frac{\pi}{4}, \frac{7 \pi}{4}\)
If cos θ = \(\frac{-1}{\sqrt{2}}\) ⇒ θ = \(\frac{3\pi}{4}, \frac{5 \pi}{4}\)
∴ Eccentric angles are θ = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\)

Question 8.
Show that the condition for a straight line y = mx + c may be a tangent to the ellipse \(\frac{\mathbf{x}^2}{\mathbf{a}^2}+\frac{\mathbf{y}^2}{\mathbf{b}^2}\) = 1 is c² = a²m² + b². (May ’06, ’02)
Solution:
Given equation of the ellipse is \(\frac{\mathbf{x}^2}{\mathbf{a}^2}+\frac{\mathbf{y}^2}{\mathbf{b}^2}\) = 1

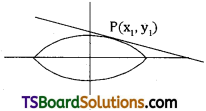
Suppose y = mx + c ……….(1)
is a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at ‘P’ is S₁ = 0
⇒ \(\frac{\mathrm{xx}_1}{\mathrm{a}^2}+\frac{\mathrm{y} \mathrm{y}_1}{\mathrm{~b}^2}-1=0\) ……..(2)
Now, (1) & (2) represent the same line.

Question 9.
Find the equation of the tangents to 9x² + 16y² = 144, which makes equal intercepts on the coordinate axes. [(TS) May ’15]
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Here a = 4, b = 3, a > b
Let the equation of the tangent which makes equal intercepts on co-ordinate axes is
x + y = k ……(1)
⇒ y = -x + k
Comparing with y = mx + c, we get
m = -1, c = k
Since eq (1) is a tangent to the given ellipse then
c² = a²m² + b²
⇒ (k)² = 16(-1)² + 9
⇒ k² = 16 + 9
⇒ k² = 25
⇒ k = ±5
Substitute the value of ‘k’ in eq (1).
∴ The equation of the tangent is x + y = ± 5
⇒ x + y ± 5 = 0

Question 10.
Find the equation of the tangent to the ellipse 2x² + y² = 8, which makes an angle π/4 with the x-axis. [(AP) May ’19]
Solution:
Given ellipse is 2x² + y² = 8
⇒ \(\frac{x^2}{4}+\frac{y^2}{8}=1\) ……..(1)
Comparing (1) with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), we get
a² = 4, b² = 8
Given that θ = \(\frac{\pi}{4}\)
The slope of the tangent is m = tan θ
= tan \(\frac{\pi}{4}\)
= 1
∴ The equation of the tangent to the given ellipse is
y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ y = 1 . x ± \(\sqrt{4(1)+8}\)
⇒ y = x ± √12
⇒ x – y ± 2√3 = 0

Question 11.
Find the equation of the tangents to the ellipse 2x² + y² = 8 which are
(i) parallel to x – 2y – 4 = 0
(ii) perpendicular to x + y + 2 = 0 [(AP) May ’19, ’17; (TS) May ’19, Mar. ’17]
Solution:
Given the equation of the ellipse is 2x² + y² = 8
⇒ \(\frac{x^2}{4}+\frac{y^2}{8}=1\)
Here a² = 4, b² = 8
(i) Given the equation of the straight line is x – 2y – 4 = 0
The equation of the tangent parallel to the line x – 2y – 4 = 0 is
x – 2y + k = 0 ……..(1)
⇒ 2y = x + k
⇒ y = \(\frac{x}{2}+\frac{k}{2}\)
Comparing with y = mx + c, we get
m = \(\frac{1}{2}\), c = \(\frac{k}{2}\)
Since eq. (1) is a tangent to the given ellipse then

Substitute the value of ‘k’ in eq. (1)
∴ The equation of the tangent is x – 2y ± 6 = 0
(ii) Given the equation of the straight line is x + y + 2 = 0
The equation of the tangent ⊥r to x + y + 2 = 0 is
x – y + k = 0 ………(2)
y = x + k
Comparing with y = mx + c we get
m = 1, c = k
Since eq. (2) is a tangent to the given ellipse then
c² = a²m² + b²
⇒ k² = 4(1)² + 8
⇒ k² = 12
⇒ k = ± 2√3
Substitute the value of ‘k’ in eq. (2)
∴ The equation of the tangent is x – y ± 2√3 = 0

Question 12.
Find the equation of tangent and normal to the ellipse 9x² + 16y² = 144 at the end of the latus rectum in the 1st quadrant. [(AP) Mar. ’15]
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Here a = 4, b = 3, a > b

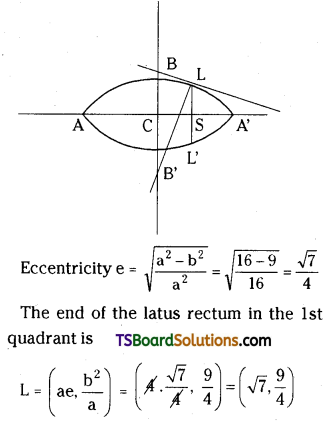
Question 13.
A circle of radius 4, is concentric with the ellipse 3x² + 13y² = 78. Prove that the common tangent is inclined to the major axis at angle π/4. [(AP) May ’18]
Solution:
Given the equation of the ellipse is 3x² + 13y² = 78
⇒ \(\frac{x^2}{26}+\frac{y^2}{6}=1\)
Here a² = 26, b² = 6, a > b

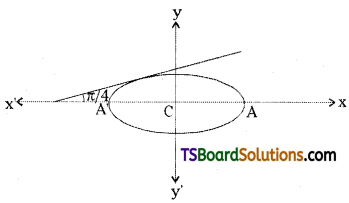
Centre of the ellipse C = (0, 0)
Centre of the circle C = (0, 0) (concentric)
given that the radius of the circle r = 4
The equation of a circle of radius 4 is concentric with the given ellipse, then
x² + y² = (4)²
⇒ x² + y² = 16
The equation of a tangent to the given ellipse is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ y = mx ± \(\sqrt{26 m^2+6}\) ……..(1)
Since (1) is a tangent to the circle x² + y² = 16, then r = d

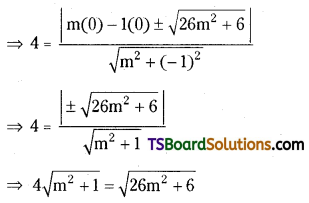
Squaring on both sides
⇒ 16(m² + 1) = 26m² + 6
⇒ 16m² + 16 = 26m² + 6
⇒ 10m² – 10 = 0
⇒ 10m² = 10
⇒ m = 1
Here, m is the slope of the tangent, then
m = tan θ
⇒ 1 = tan θ
⇒ θ = \(\frac{\pi}{4}\)
∴ A common tangent is inclined to the major axis at an angle \(\frac{\pi}{4}\).

Question 14.
If the normal at one end of the latus rectum of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) passes through one end of the minor axis, then show that e⁴ + e² = 1. (e is the eccentricity of the ellipse) [(TS) May ’17, ’14]
Solution:

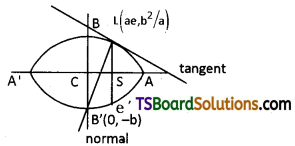
Given equation of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Let ‘L’ be the one end of the latus rectum of \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Then the coordinates of L = (ae, \(\frac{b^2}{a}\))
∴ The equation of the normal at ‘L’ is

Since eq.(1) passes through one end of the minor axis B'(0, -b) then

Question 15.
The tangent and normal to the ellipse x² + 4y² = 4 at a point P(θ) on it meets the major axis in Q and R respectively. If 0 < θ < \(\frac{\pi}{2}\) and QR = 2 then show that θ = cos^-1(2/3). [May ’16 (AP) May ’14]
Solution:

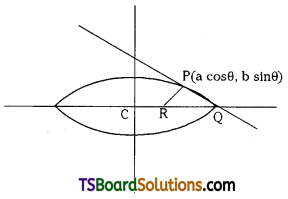
Given the equation of the ellipse is x² + 4y² = 4
⇒ \(\frac{x^2}{4}+\frac{y^2}{1}=1\)
Here a = 2, b = 1
Let ‘θ’ be the eccentric angle of ‘P’ then
P(a cos θ, b sin θ) = (2 cos θ, sin θ)
The equation of the tangent at ‘P’ is

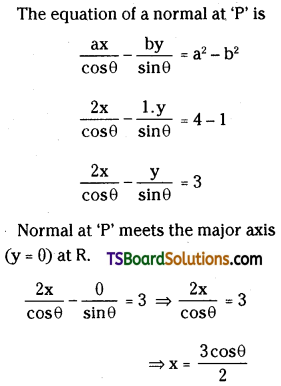
Question 16.
Find the eccentricity, coordinates of foci, length of latus rectum, and equations of directrices of the ellipse 9x² + 16y² – 36x + 32y – 92 = 0. [(TS) May & Mar. ’18, ’15]
Solution:
Given equation of the ellipse is 9x² + 16y² – 36x + 32y – 92 = 0
⇒ (9x² – 36x) + (16y² + 32y) – 92 = 0
⇒ 9(x² – 4x) + 16(y² + 2y) – 92 = 0
⇒ 9(x² – 2 . 2x + 2² – 2²) + 16(y² + 2 . 1 . y + 1² – 1²) – 92 = 0
⇒ 9((x – 2)² – 4) + 16((y + 1)² – 1) – 92 = 0
⇒ 9(x- 2)² – 36 + 16(y + 1)² – 16 – 92 = 0
⇒ 9(x – 2)² + 16 (y + 1)² – 144 = 0
⇒ 9(x – 2)² + 16(y + 1)² = 144

Question 17.
Find the length of the major axis, minor axis, latus rectum, eccentricity, coordinates of centre, foci, and the equations of directrices of the ellipse 4x² + y² – 8x + 2y + 1 = 0. [(AP) May ’18]
Solution:
Given equation of the ellipse is 4x² + y² – 8x + 2y + 1 = 0
⇒ (4x² – 8x) + (y² + 2y) + 1 = 0
⇒ 4(x² – 2x) + (y² + 2y) + 1 = 0
⇒ 4((x)² – 2x . 1 + 1² – 1²) + ((y)² + 2 . y . 1 + 1² – 1²) + 1 = 0
⇒ 4((x – 1)² – 1) + ((y + 1)² – 1) + 1 = o
⇒ 4(x – 1)² – 4 + (y + 1)² – 1 + 1 = 0
⇒ 4(x – 1)² + (y + 1)² = 4
⇒ \(\frac{4(x-1)^2}{4}+\frac{(y+1)^2}{4}=1\)
⇒ \(\frac{(x-1)^2}{1}+\frac{(y-(-1))^2}{4}=1\)
Comparing with \(\frac{(\mathrm{x}-\mathrm{h})^2}{\mathrm{a}^2}+\frac{(\mathrm{y}-\mathrm{k})^2}{\mathrm{~b}^2}=1\)
we get h = 1, k = -1, a = 1, b = 2, a < b
The length of the major axis = 2b = 2(2) = 4
The length of the minor axis = 2a = 2(1) = 2
The length of latus rectum = \(\frac{2 a^2}{b}=\frac{2 \cdot 1}{2}\) = 1

Question 18.
Find the eccentricity, coordinates of foci, length of latus rectum, and equations of directrices of the ellipse 3x² + y² – 6x – 2y – 5 = 0. [(AP) May ’15]
Solution:
Given equation of the ellipse is 3x² + y² – 6x – 2y – 5 = 0
⇒ (3x² – 6x) + (y² – 2y) – 5 = 0
⇒ 3(x² – 2x) + (y² – 2y) – 5 = 0
⇒ 3((x)² – 2 . 1 . x + 1² – 1²) + ((y)² – 2 . 1 . y + 1² – 1²) – 5 = 0
⇒ 3((x – 1)² – 1) + ((y – 1)² – 1) – 5 = 0
⇒ 3(x – 1)² – 3 + (y – 1)² – 1 – 5 = 0
⇒ 3(x – 1)² + (y – 1)² – 9 = 0
⇒ 3(x – 1)² + (y – 1)² = 9
⇒ \(\frac{(x-1)^2}{9 / 3}+\frac{(y-1)^2}{9}=1\)
⇒ \(\frac{(x-1)^2}{3}+\frac{(y-1)^2}{9}=1\)

Question 19.
Find the equation of an ellipse in the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\), given that centre (0, -3), e = \(\frac{2}{3}\), semi-minor axis 5.
Solution:
The equation of the ellipse is
\(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\) ………(1)
Given that Centre C(h, k) = (0, -3)
Eccentricity e = \(\frac{2}{3}\)
Case (i): If a > b, the length of the semi-minor axis b = 5
We know that b² = a²(1 – e²)
25 = a²(1 – \(\frac{4}{9}\))

Question 20.
Find the equation of the ellipse in the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\), given that centre (2, -1) one end of the major axis (2, -5), e = \(\frac{1}{3}\).
Solution:
The equation of the ellipse is
\(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\) …….(1)

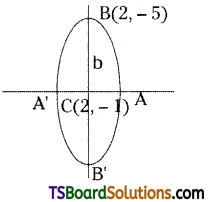
Given that
Centre C(h, k) = (2, -1)
One end of the major axis B = (2, -5)
Eccentricity e = \(\frac{1}{3}\)
In C, B, the x-coordinates are equal, then the major axis is parallel to the y-axis, i.e., a < b

Question 21.
Prove that the equation of the chord joining the points ‘α’ and ‘β’ on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is \(\frac{x}{a} \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \sin \left(\frac{\alpha+\beta}{2}\right)\) = \(\cos \left(\frac{\alpha-\beta}{2}\right)\) [(TS) May ’16]
Solution:
Given equation of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Given points on the ellipse is P(a cos α, b sin α), Q(a cos β, b sin β)

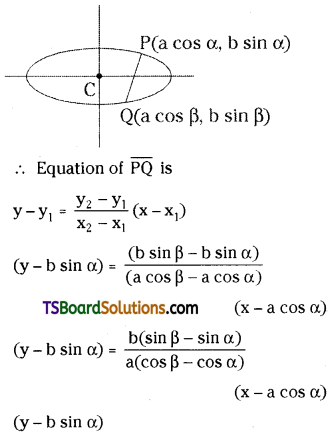
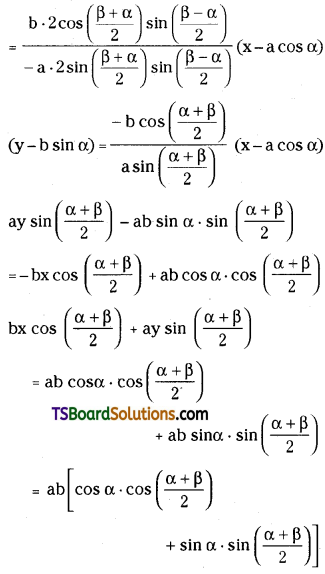
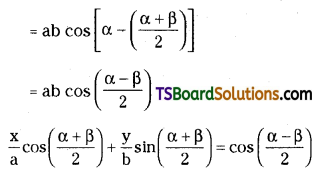
Question 22.
Show that the foot of the perpendicular drawn from centre to any tangent to the ellipse lies on the curve (x² + y²) = a²x² + b²y².
Solution:
Let, the equation of the ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
Let, P(x₁, y₁) be the foot of the perpendicular drawn from the centre on any tangent to the ellipse.

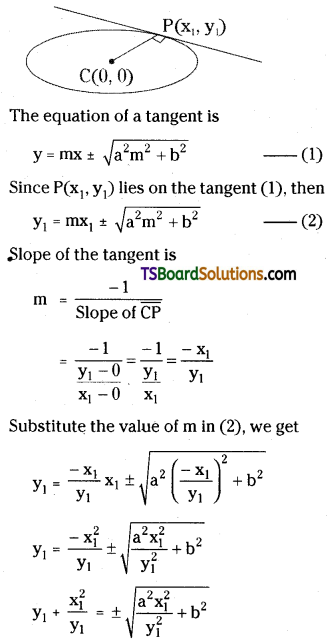
Question 23.
Show that the point of intersection of the perpendicular tangent to an ellipse lies on a circle. [(AP) Mar. ’16]
Solution:

Let the equation of the ellipse be
S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0
Let P(x₁, y₁) be the point of intersection of ⊥r tangent drawn to the ellipse.
Let y = mx ± \(\sqrt{a^2 m^2+b^2}\) be a tangent to the ellipse S = 0 passing through ‘P’, then
y₁ = mx₁ ± \(\sqrt{a^2 m^2+b^2}\)
y₁ – mx₁ = ± \(\sqrt{a^2 m^2+b^2}\)
Squaring on both sides,

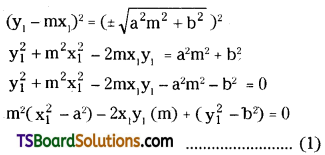
If m₁, m₂ are the slopes of the tangents through ‘P’ then m₁, m₂ are the roots of (1).
Since the tangents through ‘P’ are ⊥r then
m₁m₂ = -1
⇒ \(\frac{y_1^2-b^2}{x_1^2-a^2}=-1\)
⇒ \(y_1^2-b^2=-x_1^2+a^2\)
⇒ \(\mathrm{x}_1^2+\mathrm{y}_1^2=\mathrm{a}^2+\mathrm{b}^2\)
∴ P lies on x² + y² = a² + b² which is the circle with centre as the origin, the centre of the ellipse.

Question 24.
Show that the locus of the feet of the perpendiculars drawn from foci to any tangent of the ellipse is the auxiliary circle. [(AP) Mar. ’19, ’17]
Solution:

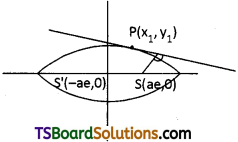
Let the equation of the ellipse be
S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0
Let P(x₁, y₁) be the foot of the ⊥r drawn from either of the foci to a tangent.
The equation of the tangent to the ellipse S = 0 is
y = mx ± \(\sqrt{a^2 m^2+b^2}\) ……..(1)
The equation to the perpendicular from either focus (±ae, 0) on this tangent is

∴ ‘P’ lies on x² + y² = a² which is a circle with centre as the origin, the centre of the ellipse.

Question 25.
Prove that the equation of an ellipse in the standard form is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). (Mar. ’95)
Solution:

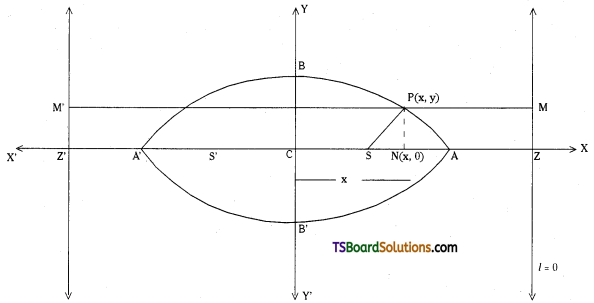
Let ‘S’ be the focus, ‘e’ be the eccentricity and l = 0 be the directrix of the ellipse.
Let ‘P’ be a point on the ellipse.
Let M, Z be the projections (foot of the ⊥rs) of P, S on the directrix L = 0 respectively.
Let ‘M’ be the projection of ‘P’ on ‘SZ’.
Since e < 1 we can divide SZ both internally and externally in the ratio e : 1.
Let A, A’ be the points of division of SZ in the ratio e : 1 internally and externally respectively.
Let AA’ = 2a
Let ‘C’ be the midpoint of AA’.
Points A, A’ lies on the ellipse and \(\frac{\mathrm{SA}}{\mathrm{AZ}}=\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
Now \(\frac{S A}{A Z}=\frac{e}{1}\)
⇒ SA = e AZ
⇒ CA – CS = e (CZ – CA) ……..(1)
Also \(\frac{\mathrm{SA}^{\prime}}{\mathrm{ZA}^{\prime}}=\frac{\mathrm{e}}{1}\)
⇒ SA’ = e ZA’
CS + CA’ = e (CA’ + CZ) ……..(2)
Now (1) + (2)
⇒ CA – CS + CS + CA’ = e (CZ – CA) + e(CZ + CA’)
⇒ CA + CA’ = e (CZ – CA) + e (CZ + CA’)
⇒ CA + CA’ = e (2CZ – CA + CA’)
Since ‘C’ is the midpoint of AA’ then CA = CA’
CA + CA = e (2CZ – CA + CA)
⇒ 2CA = 2e CZ
⇒ CA = e CZ
⇒ a = e CZ
⇒ CZ = \(\frac{a}{e}\)
∴ Equation of the directrix is x = \(\frac{a}{e}\)
(1) – (2)
⇒ CA – CS – CS + CA’ = e (CZ – CA) + e(CZ + CZ)
⇒ CA – CS – CS – CA’ = e (CZ – CA – CA – CZ)
⇒ CA – 2CS – CA’ = e(-CA – CA’)
Since ‘C’ is the midpoint at AA’ then CA = CA’
CA – 2CS – CA = e(-CA – CA)
⇒ -2CS = e(-2CA)
⇒ CS = e CA
⇒ CS = eQ
∴ Co-ordinates of focus ‘S’ are (ae, 0)
Take CS, the principal axis of the ellipse as the X-axis, and QS ⊥r to the CX as Y-axis then S = (ae, 0) and the ellipse is in standard form.
Let P = (x, y)
Now PM = NZ = CZ – CN = \(\frac{a}{e}\) – x
‘P’ lies on the ellipse then \(\frac{SP}{PM}\) = e
SP = e . PM

Question 26.
If the length of the latus rectum is equal to half of its minor axis of an ellipse in the standard form, then find the eccentricity of the ellipse. (May, Mar. ’10)
Solution:
Let the equation of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
The length of the latus rectum = \(\frac{2 b^2}{a}\)
Length of minor axis = 2b
Given that the length of the latus rectum is equal to half of its minor axis then

Question 27.
Find the eccentricity of the ellipse (in the standard form), if the length of the latus rectum is equal to half of its major axis.
Solution:
Let the equation of the ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
The length of the latus rectum = \(\frac{2 b^2}{a}\)
Length of the major axis = 2a
Given that the length of the latus rectum is equal to half of its major axis then

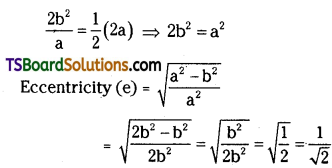
Question 28.
Find the equation of tangent and normal to the ellipse x² + 8y² = 33 at (-1, 2). [(TS) Mar. ’20; May ’16]
Solution:
Given the equation of the ellipse is x² + 8y² = 33
Let the given point P(x₁, y₁) = (-1, 2)
The equation of the tangent at ‘P’ is S₁ = 0
⇒ xx₁ + 8yy₁ = 33
⇒ x(-1) + 8y(2) = 33
⇒ -x + 16y = 33
⇒ x – 16y + 33 = 0
Slope of the tangent at P’ is m = \(\frac{-1}{-16}=\frac{1}{16}\)
Slope of the normal at ‘P’ = \(\frac{-1}{m}=\frac{-1}{\frac{1}{16}}\) = -16
The equation of the normal at ‘P’ is
y – y₁ = \(\frac{-1}{m}\)(x – x₁)
⇒ y – 2 = -16(x + 1)
⇒ y – 2 = -16x – 16
⇒ 16x + y + 14 = 0

Question 29.
Find the value of ‘k’ if 4x + y + k = 0 is tangent to the ellipse x² + 3y² = 3.
Solution:
Given the equation of the ellipse is x² + 3y² = 3
⇒ \(\frac{x^2}{3}+\frac{y^2}{1}=1\)
Here a² = 3, b² = 1
Given the equation of the straight line is
4x + y + k = 0 ……..(1)
y = -4x – k
Comparing with y = mx + c we get
m = -4, c = -k
Since eq. (1) is a tangent to the given ellipse then c² = a²m² + b²
⇒ (-k)² = 3(-4)² + 1
⇒ k² = 49
⇒ k = ±7

Question 30.
Find the condition for the line x cos α + y sin α = p to be a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). [(AP) Mar. ’20, ’14]
Solution:
Given equation of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Given the equation of the straight line is x cos α + y sin α = p
y sin α = -x cos α + p

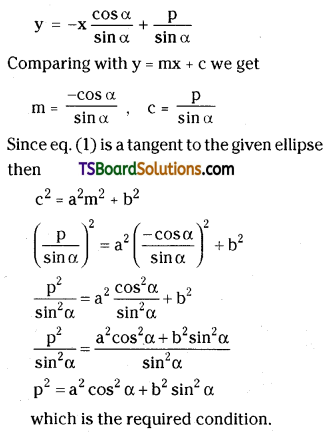
Question 31.
If the length of the major axis of an ellipse is three times the length, of its minor axis, then find the eccentricity of the ellipse.
Solution:
In an ellipse
Length of major axis = 2a
Length of minor axis = 2b
Given that length of the major axis = 2(length of the minor axis)

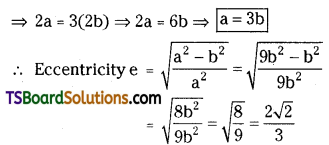
Question 32.
Find the equation of the auxiliary circle of the ellipse 9x² + 16y² = 144.
Solution:
Given ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Here a² = 16, b² = 9 (a > b)
∴ The equation of an auxiliary circle is x² + y² = a²
⇒ x² + y² = 16

Question 33.
Find the equation of the director circle of the ellipse 9x² + 25y² = 225.
Solution:
Given ellipse is 9x² + 25y² = 225
⇒ \(\frac{x^2}{25}+\frac{y^2}{9}=1\)
Here a² = 25, b² = 9
∴ Equation of director circle is x² + y² = a² + b²
⇒ x² + y² = 25 + 9
⇒ x² + y² = 34

Question 34.
If P(x, y) is any point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b) whose foci are ‘S’ and S’ then show that SP + S’P is a constant. (Mar. ’13, May, Mar. ’93)
Solution:

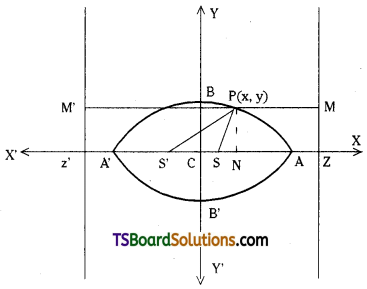
The equation of the ellipse is given as
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
Let S, S’ be the foci and ZM, Z’M’ be the corresponding directrices.
Join SP and S’P.
Draw PN ⊥r to X-axis and M’MP ⊥r to the two directrices.
By the definition of the ellipse,
\(\frac{\mathrm{SP}}{\mathrm{PM}}\) = e
⇒ SP = e PM
= e NZ
= e (CZ – CN)
= e(\(\frac{a}{e}\) – x)
and \(\frac{\mathrm{S}^{\prime} \mathrm{P}}{\mathrm{PM}^{\prime}}\) = e
S’P = e PM’
= e(NZ’)
= e(CN + CZ’)
= e(x + \(\frac{a}{e}\))
Now SP + S’P
= \(e\left(\frac{a}{e}-x\right)+e\left(x+\frac{a}{e}\right)\)
= a – ex + ex + a
= 2a (constant)
= length of the major axis

Question 35.
The orbit of the Earth is an ellipse with eccentricity \(\frac{1}{60}\) with the sun at one of its foci, the major axis being approximately 186 × 10⁶ miles in length. Find the shortest and longest distance of the earth from the sun.
Solution:
Assume that the orbit of the earth is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
Since the major axis is 186 × 106 miles
2a = 186 × 10⁶ miles
∴ a = 93 × 10⁶ miles
If ’e’ be the eccentricity of the orbit, then
e = \(\frac{1}{60}\)
we know that the longest and shortest distances from the earth from the sun are respectively.
a + ae and a – ae.
The longest distance = a + ae
= a(1 + e)
= 93 × 10⁶ (1 + \(\frac{1}{60}\))
= 9455 × 10⁴ miles
The shortest distance = a – ae
= a(1 – e)
= 93 × 10⁶ (1 – \(\frac{1}{60}\))
= 9145 × 10⁴ miles

Question 36.
A man running on a race course notices that the sum of the distances between the two flag posts is always 10 m and the distance between the flag posts is 8m. Find the equation of the race course traced by the man.
Solution:
Let S, S’ be the two flag posts on the x-axis, so that ‘O’ is the midpoint of S, S’.

Given that, the distance between the two flag posts = 8
⇒ 2ae = 8
⇒ ae = 4
∴ S(ae, 0) = (4, 0)
S'(-ae, 0) = (-4, 0)
Let P(x, y) be any point on the locus given that,
the sum of the distances of two flag posts = 10
SP + S’P = 10
SP = 10 – S’P

Question 37.
Find the equation of the ellipse in the standard form, if it passes through the points (-2, 2) and (3, -1). [Mar. ’17 (TS)]
Solution:
Let the equation of the ellipse in the standard form is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b) ……(1)
Since equation (1) passes through the point (-2, 2) then

Question 38.
Find the equation of tangent and normal to the ellipse x² + 2y² – 4x + 12y + 14 = 0 at (2, -1).
Solution:
Given equation of the ellipse is x² + 2y² – 4x + 12y + 14 = 0
Let the given point P(x₁, y₁) = (2, -1)
The equation of the tangent at ‘P’ is S₁ = 0
⇒ xx₁ + 2yy₁ – 2(x + x₁) + 6 (y + y₁) + 14 = 0
⇒ x(2) + 2y(-1) – 2(x + 2) + 6(y – 1) + 14 = 0
⇒ 2x – 2y – 2x – 4 + 6y – 6 + 14 = 0
⇒ 4y + 4 = 0
⇒ y + 1 = 0
The slope of the tangent at ‘P’ is m = \(\frac{-0}{1}\) = 0
The slope of the normal at ‘P’ is \(\frac{-1}{\mathrm{~m}}=\frac{-1}{0}\)
∴ The equation of the normal at ‘P’ is
y – y₁ = \(\frac{-1}{m}\)(x – x₁)
⇒ y + 1 = \(\frac{-1}{0}\) (x – 2)
⇒ 0 = -x + 2
⇒ x – 2 = 0

Question 39.
Find the equations of tangents to the ellipse 2x² + 3y² = 11 at the points whose ordinate is 1. [(TS) Mar. ’19, ’16]
Solution:
Given the equation of the ellipse is 2x² + 3y² = 11
given that y = 1
2x² + 3 = 11
⇒ 2x² = 8
⇒ x² = 4
⇒ x = ±2
Points of contact P(2, 1) & Q(-2, 1)
Case (i): P(2, 1)
The equation of the tangent is S₁ = 0
⇒ 2xx₁ + 3yy₁ = 11
⇒ 2x(2) + 3y(1) = 11
⇒ 4x + 3y = 11
Case (ii): Q(-2, 1)
The equation of the tangent is S₁ = 0
⇒ 2xx₁ + 3yy₁ = 11
⇒ 2x(-2) + 3y(1) = 11
⇒ -4x + 3y = 11
⇒ 4x – 3y + 11 = 0

Question 40.
Find the equations of the tangents to the ellipse x² + 2y² = 3 drawn from the point (1, 2) and also find the angle between them.
Solution:
Given the equation of the ellipse is x² + 2y² = 3

Let the given point P(x₁, y₁) = (1, 2)
The equation of the pair of tangents to the ellipse x² + 2y² = 3 drawn from the point P(1, 2) is S . S₁₁ = \(\mathrm{S}_1{ }^2\)
⇒ (x² + 2y² – 3) \(\left(x_1{ }^2+2 y_1{ }^2-3\right)\) = (xx₁ + 2yy₁ – 3)²
⇒ (x² + 2y² – 3)[(1)² + 2(2)² – 3)] = [x(1) + 2y(2) – 3]²
⇒ (x² + 2y² – 3) (1 + 8 – 3) = (x + 4y – 3)²
⇒ (x² + 2y² – 3) (6) = (x + 4y – 3)²
⇒ 6x² + 12y² – 18 = x² + 16y² + 9 + 8xy – 24y – 6x
⇒ 5x² – 8xy – 4y² + 6x + 24y – 27 = 0
Consider 5x² – 8xy – 4y² = 0
⇒ 5x² – 10xy + 2xy – 4y² = 0
⇒ 5x(x – 2y) + 2y(x – 2y) = 0
⇒ (x – 2y) (5x + 2y) = 0
⇒ x – 2y = 0, 5x + 2y = 0
∴ 5x² – 8xy – 4y² + 6x + 24y – 27 = (x – 2y + l) (5x + 2y + k)
Comparing the coefficient of x on both sides, we get ‘
k + 5l = 6 ………(1)
Comparing the coefficient of y on both sides, we get
-2k + 2l = 24
k – l = -12 ………(2)
Solve (1) & (2)

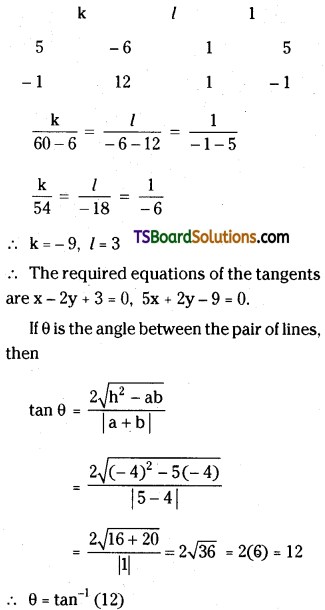
Question 41.
Find the condition for the line lx + my + n = 0 to be a tangent to the ellipse \(\frac{\mathbf{x}^2}{a^2}+\frac{y^2}{b^2}=1\). [(AP) May ’15]
Solution:

Given equation of the ellipse is \(\frac{\mathbf{x}^2}{a^2}+\frac{y^2}{b^2}=1\)
Suppose lx + my + n = 0 ……..(1)
is a tangent to the ellipse \(\frac{\mathbf{x}^2}{a^2}+\frac{y^2}{b^2}=1\)
Let P(x₁, y₁) be the point of contact.
The equation of the tangent at ‘P’ is S₁ = 0
\(\frac{x_1}{a^2}+\frac{y_1}{b^2}-1=0\) ……..(2)
Now (1) & (2) represent the same line.

Question 42.
Find the condition for the line lx + my + n = 0 to be normal to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). [Mar. ’01, ’91]
Solution:

Given the equation of the ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) …….(1)
Suppose lx + my + n = 0 is a normal to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Let P(a cos θ, b sin θ) be a point on the ellipse.
∴ The equation of the normal at P(θ) is
\(\frac{a x}{\cos \theta}-\frac{b y}{\sin \theta}=a^2-b^2\) ……..(2)
Now (1) & (2) represent the same line.

Question 43.
‘C’ is the centre, AA’ and BB’ are the major axis and minor axis of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). If PN is the ordinate of a point P on the ellipse, then show that \(\frac{(P N)^2}{\left(A^{\prime} N\right)(A N)}=\frac{(B C)^2}{(C A)^2}\)
Solution:
Let P(θ) = P(a cos θ, b sin θ) be a point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
∴ PN = b sin θ, CN = a cos θ and CA = CA’ = a, CB = CB’ = b
LHS

Question 44.
If a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b) meets its major axis and minor axis at M and N respectively, then prove that \(\frac{a^2}{(\mathrm{CM})^2}+\frac{b^2}{(\mathrm{CN})^2}=1\) where c is the centre of the ellipse. [(TS) May ’18; (AP) Mar. ’18]
Solution:
Let P(θ) = P (a cos θ, b sin θ)
be a point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
The equation of tangent at P(θ) is
\(\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}=1 \Rightarrow \frac{x}{\left(\frac{a}{\cos \theta}\right)}+\frac{y}{\left(\frac{b}{\sin \theta}\right)}=1\)
It meets the major axis (x-axis) and minor axis (y-axis) at M and N respectively.

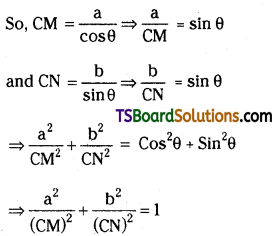
Question 45.
If PN is the ordinate of a point P on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and the tangent at P meets the x-axis at T, then show that (CN) (CT) = a² where C is the centre of the ellipse.
Solution:
Given equation of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Let P(θ) = (a cos θ, b sin θ) be a point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

The equation of the tangent at P(θ) is
\(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\)
⇒ \(\frac{x}{\frac{a}{\cos \theta}}+\frac{y}{\frac{b}{\sin \theta}}=1\)
This tangent meets the x-axis at T, then x-intercept CT = \(\frac{a}{\cos \theta}\)
The ordinate of P is PN = b sin θ
The absissa of P is CN = a cos θ
LHS = CN . CT
= a cos θ . \(\frac{a}{\cos \theta}\)
= a²
= RHS
∴ CN . CT = a²

Question 46.
Show that the equation of the normal to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) at P(x1, y1) is \(\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2\). (May ’98)
Solution:

Question 47.
Show that the equation of the tangent at P(θ) on the ellipse S = 0 is \(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\). (Mar. ’99)
Solution:

Let the equation of the ellipse be
S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0
Given point P = (a cos θ, b sin θ)
The equation of the tangent at ‘P’ is S1 = 0

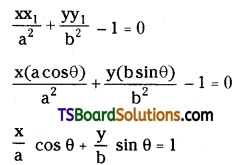
Question 48.
S and T are the foci of an ellipse and B is one end of the minor axis. If STB is an equilateral triangle, then find the eccentricity of the ellipse. [(AP) Mar. ’20]
Solution:

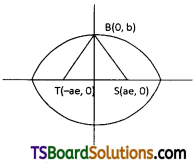
Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b) be an ellipse, whose foci are ‘S’ and ‘T’.
‘B’ is one end of the minor axis such that STB is an equilateral triangle.
Then SB = ST = TB.
We have S = (ae, 0), T = (-ae, 0) and B = (0, b)
Consider SB = ST
⇒ SB² = ST²
⇒ (ae – 0)² + (0 – b)² = (ae + ae)² + (0 – 0)²
⇒ a²e² + b² = (2ae)²
⇒ a²e² + a²(1 – e²) = 4a²e²
⇒ e² + (1 – e²) = 4e²
⇒ 4e² = 1
⇒ e² = \(\frac{1}{4}\)
⇒ e = \(\frac{1}{2}\)
∴ Eccentricity of the ellipse, e = \(\frac{1}{2}\)

Question 49.
If the ends of the major axis of an ellipse are (5, 0) and (-5, 0). Find the equation of the ellipse in the standard form if its focus lies on the line 3x – 5y – 9 = 0.
Solution:
Let the equation of the ellipse in the standard form is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
Given that the ends of the major axis of an ellipse are A = (a, 0) = (5, 0)
A’ = (-a, 0) = (-5, 0)
∴ a = 5
Given the equation of the straight line is 3x – 5y – 9 = 0
Focus ‘S’ = (ae, 0)
Since focus ‘S’ (ae, 0) lies on the line 3x – 5y – 9 = 0 then
3(ae) – 5(0) – 9 = 0
⇒ 3ae – 9 = 0
⇒ ae = 3
We know that b² = a²(1 – e²)
= a² – a²e²
= 5² – 3²
b² = 16
∴ The equation of the ellipse is \(\frac{x^2}{25}+\frac{y^2}{16}=1\)
⇒ 16x² + 25y² = 400

Question 50.
Find the coordinates of the points on the ellipse x² + 3y² = 37 at which the normal is parallel to the line 6x – 5y = 2.
Solution:
Given the equation of the ellipse is x² + 3y² = 37

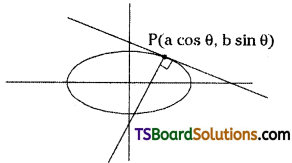
Let P(a cos θ, b sin θ) be a point on the ellipse
The equation of the tangent at P(θ) is
\(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\)
The slope of the tangent at P is

Given the equation of the straight line is 6x – 5y = 2
Slope of the line is m = \(\frac{-6}{-5}=\frac{6}{5}\)
Since the normal is parallel to the line 6x – 5y = 2, the slopes are equal.

Since tan θ is positive, then P = (5, 2), (-5, -2).
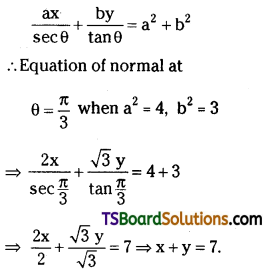