TS Inter Second Year Maths 2B Hyperbola Important Questions Very Short Answer Type

Students must practice these Maths 2B Important Questions TS Inter Second Year Maths 2B Hyperbola Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2B Hyperbola Important Questions Very Short Answer Type

Question 1.
Find the equation to the hyperbola whose foci are (4, 2) and (8, 2) and whose eccentricity is 2. (Mar. ’09)
Solution:
Given that foci are S = (4, 2), S’ = (8, 2)
eccentricity e = 2
In foci, Y-coordinates are equal then the transverse axis is parallel to X-axis.
∴ The equation of the hyperbola is of the form \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\) …….(1)
The distance between the foci is
SS’ = \(\sqrt{(4-8)^2+(2-2)^2}\) = √16 = 4
⇒ 2ae = 4
⇒ 2a(2) = 4
⇒ a = 1
Centre = Midpoint of S and S’
(h, k) = \(\left(\frac{4+8}{2}, \frac{2+2}{2}\right)=\left(\frac{12}{2}, \frac{4}{2}\right)\) = (6, 2)
∴ (h, k) = (6, 2)
We know that b² = a²(e² – 1)
⇒ b² = 1(4 – 1)
⇒ b² = 3
∴ The required equation of the hyperbola is \(\frac{(\mathrm{x}-6)^2}{1}-\frac{(\mathrm{y}-2)^2}{3}=1\)
⇒ 3(x – 6)² – (y – 2)² = 3
⇒ 3(x² + 36 – 12x) – (y² + 4 – 4y) = 3
⇒ 3x² – y² + 108 – 36x – 4 + 4y = 3
⇒ 3x² – y² – 36x + 4y + 101 = 0

Question 2.
Find the equation of the hyperbola whose foci are (±5, 0) and the transverse axis is of length 8. [(AP) May ’18, (TS) Mar. ’16]
Solution:
Given that foci = (±5, 0)
(±ae, 0) = (±5, 0)
∴ ae = 5 ……..(1)
The length of the transverse axis = 8
⇒ 2a = 8
⇒ a = 4
From (1),
4e = 5
⇒ e = \(\frac{5}{4}\)
We know that b² = a²(e² – 1)
= 16(\(\frac{25}{16}\) – 1)
= 16(\(\frac{9}{16}\))
= 9
∴ The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
⇒ 9x² – 16y² = 144

Question 3.
If 3x – 4y + k = 0 is a tangent to x² – 4y² = 5. Find the value of k. [(AP) Mar. ’20; (TS) Mar. ’18, ’17; May ’17]
Solution:
Given the equation of the hyperbola is x² – 4y² = 5
⇒ \(\frac{x^2}{5}-\frac{4 y^2}{5}=1\)
⇒ \(\frac{x^2}{5}-\frac{y^2}{5 / 4}=1\)
Here a² = 5, b² = 5/4
Given the equation of the straight line is
3x – 4y + k = 0 ………(1)
4y = 3x + k
y = \(\frac{3}{4} x+\frac{k}{4}\)
Comparing with y = mx + c, we get
m = 3/4, c = k/4
Since equation (1) is a tangent to the given hyperbola then
c² = a²m² – b²
⇒ \(\left(\frac{k}{4}\right)^2=5\left(\frac{3}{4}\right)^2-\frac{5}{4}\)
⇒ \(\frac{k^2}{16}=5 \cdot \frac{9}{16}-\frac{5}{4}\)
⇒ \(\frac{\mathbf{k}^2}{16}=\frac{45-20}{16}\)
⇒ k² = 25
⇒ k = ±5

Question 4.
If e, e₁ is the eccentricities of a hyperbola and its conjugate hyperbola. Prove that \(\frac{1}{e^2}+\frac{1}{e_1^2}=1\). [(TS) May ’18, Mar. ’17]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
‘e’ is the eccentricity of the hyperbola then
e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)
The equation of the conjugate hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\)
‘e₁‘ is the eccentricity of the conjugate hyperbola then
e₁ = \(\sqrt{\frac{a^2+b^2}{b^2}}\)

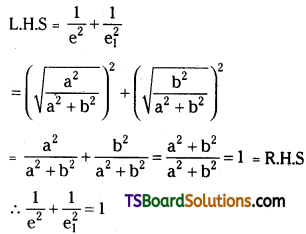
Question 5.
If the eccentricity of a hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate hyperbola. [(AP) May ’19, ’16, ’15; (AP) Mar. ’17, ’16; (TS) Mar. ’19, ’15; (TS) May ’15; Mar. ’13; May ’13]
Solution:
The equation of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
Given that the eccentricity of the hyperbola
e = \(\frac{5}{4}\)
The equation of the conjugate hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\)
The eccentricity of the conjugate hyperbola e’ = ?

∴ Eccentricity of the conjugate hyperbola = \(\frac{5}{3}\)

Question 6.
If the lines 3x – 4y = 12 and 3x + 4y = 12 meet on a hyperbola S = 0, then find the eccentricity of the hyperbola S = 0.
Solution:
Given equations of the lines are
3x – 4y = 12 ……….(1)
3x + 4y = 12 ………(2)
The combined equation of lines (1) and (2) is
(3x – 4y) (3x + 4y) = 144
⇒ 9×2 – 16y2 = 144
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
which represents a hyperbola of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
∴ a² = 16, b² = 9
∴ Eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}\)
= \(\sqrt{\frac{16+9}{16}}\)
= \(\frac{5}{4}\)

Question 7.
Find the product of lengths of the perpendiculars from any point on the hyperbola \(\frac{x^2}{16}-\frac{y^2}{9}=1\) to its asymptotes. [(TS) May ’19, ’16; (AP) Mar. ’19]
Solution:
Given equation of the hyperbola is \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
Here a² = 16, b² = 9
The product of the ⊥ar distances from any point on a hyperbola to its asymptotes = \(\frac{a^2 b^2}{a^2+b^2}\)
= \(\frac{16 \cdot 9}{16+9}\)
= \(\frac{144}{25}\)

Question 8.
Show that the Angle between the two asymptotes of a hyperbola \(\frac{\mathbf{x}^2}{\mathbf{a}^2}-\frac{\mathbf{y}^2}{b^2}=1\) is 2tan^-1(\(\frac{b}{a}\)) or 2 sec^-1(e).
Solution:
Let the equation of hyperbola be \(\frac{\mathbf{x}^2}{\mathbf{a}^2}-\frac{\mathbf{y}^2}{b^2}=1\)
The asymptotes of hyperbola are
y = ±\(\frac{b}{a}\)x where m₁ = \(\frac{b}{a}\) and m₂ = \(-\frac{b}{a}\).
If θ is the angle between asymptotes of the hyperbola then

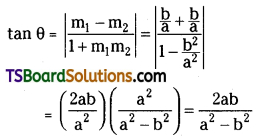
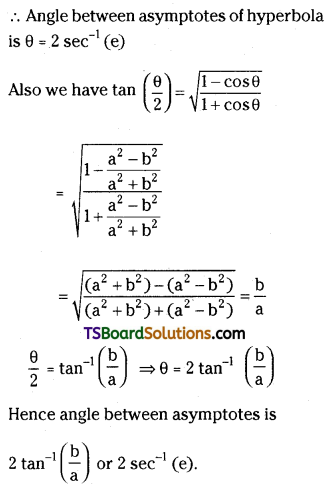
Question 9.
If the angle between asymptotes is 30° then find its eccentricity. [(TS) Mar. ’20; (AP) May ’17; ’14]
Solution:
The angle between asymptotes of the hyperbola

Question 10.
Define rectangular hyperbola and find its eccentricity. [(AP) Mar. ’15, ’14]
Solution:
Rectangular Hyperbola: If in a hyperbola the length of the transverse axis (2a) is equal to the length of the conjugate axis (2b), the hyperbola is called a rectangular hyperbola.
Its equation is x² – y² = a² [∵ a = b]
In this case
e² = \(\frac{a^2+b^2}{a^2}=\frac{2 a^2}{a^2}=2\)
⇒ e = √2
∴ The eccentricity of a rectangular hyperbola is √2.

Question 11.
Find the equation of normal at \(\theta=\frac{\pi}{3}\) to the hyperbola 3x² – 4y² = 12.
Solution:
The given equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
The equation of normal at P(a sec θ, b tan θ) to the hyperbola S = 0 is

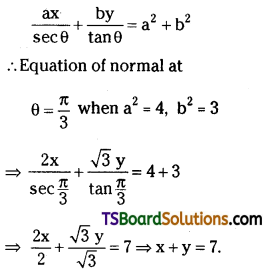
Question 12.
Find the equation of the hyperbola whose asymptotes are 3x = ±5y and the vertices (±5, 0).
Solution:
The asymptote equation is given by 3x – 5y = 0 and 3x + 5y = 0.
∴ The equation of hyperbola is of the form (3x – 5y) (3x + 5y) = k
⇒ 9x² – 25y² = k
If the hyperbola passes through the vertex (±5, 0) then
9(25) = k
⇒ k = 225
Hence the equation of asymptotes of a hyperbola is 9x² – 25y² = 225

Question 13.
Prove that the equations of the asymptotes of the hyperbola S = 0 are \(\frac{x}{a} \pm \frac{y}{b}=0\).
Solution:
Let the equation of the hyperbola is
S = \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\) ……..(1)
The equation of the tangent at ‘m’ is
y = mx + \(\sqrt{a^2 m^2-b^2}\) …….(2)
The point of contact of (1) & (2) is
\(\left(\frac{-a^2 m}{\sqrt{a^2 m^2-b^2}}, \frac{-b^2}{\sqrt{a^2 m^2-b^2}}\right)\)
If (2) is an asymptote, then it touches the hyperbola at infinity
Hence a²m² – b² = 0
⇒ m = ±\(\frac{b}{a}\)
∴ The asymptotes are y = ±\(\frac{b}{a}\)x
⇒ \(\frac{x}{a} \pm \frac{y}{b}=0\)

Question 14.
Find the eccentricity and length of the latus rectum of the hyperbola 4x² – 9y² = 27. (Mar. ’06)
Solution:
Given the equation of the hyperbola is 4x² – 9y² = 27

Question 15.
Find the foci of the hyperbola 9x² – 16y² + 72x – 32y – 16 = 0. (May ’01)
Solution:
Given equation of the hyperbola is 9x² – 16y² + 72x – 32y – 16 = 0
⇒ 9(x² + 8x) – 16(y² + 2y) = 16
⇒ 9(x² + 8x + 16) – 16(y² + 2y + 1) = 16 + 144 – 16
⇒ 9(x + 4)² – 16(y + 1)² = 144