TS Inter Second Year Maths 2A Random Variables and Probability Distributions Important Questions Very Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Random Variables and Probability Distributions Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Random Variables and Probability Distributions Important Questions Very Short Answer Type

Question 1.
Define Binomial distribution. [Mar. ’92, May ’94]
Solution:
Definition:
Let n’ be a positive integer and p be a real number such that 0 ≤ p ≤ 1. A random variable, X with range {0, 1, 2, ……., n} is said to follow (or have) binomial distribution (or) Bernoulli distribution with parameters n and p,
if P(X = r) = \({ }^n C_r\) p^rq^n-r for r = 0, 1, 2, , n where q = 1 – p.

Question 2.
8 coins are tossed simultaneously. Find the probability of getting atleast 6 heads.
Solution:
X follows binomial distribution.
Let, X be the no. of heads getting when 8 coins are tossed.
In the experiment of tossing a coin,
the probability of getting a head, p = \(\frac{1}{2}\)
the probability of getting a tail, q = 1 – p
= 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\), n = 8
The probability of getting atleast 6 heads =
P(X ≥ 6) = P(X = 6) + P(X = 7) + P(X = 8)
We have, P(X = r) = \({ }^n C_r\) p^rq^n-r

Question 3.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1).
[TS – Mar. ’17, ’15; AP – May 2015; Mar. ’11, ’08, May ’11] [AP – Mar. 2016; AP & TS – Mar. 2019]
Solution:
X follows binomial distribution.
In binomial distribution, mean = 4
np = 4 …………(1)
variance = 3
npq = 3 …………….(2)
Now, \(\frac{(2)}{(1)} \Rightarrow \frac{n p q}{n p}=\frac{3}{4}\)
q = \(\frac{3}{4}\)
p = 1 – q
= 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
p = \(\frac{1}{4}\)
From (1), n(\(\frac{1}{4}\)) = 4
n = 16
Parameters are n = 16, p = \(\frac{1}{4}\)
Distribution = (q + p)ⁿ
= \(\left(\frac{3}{4}+\frac{1}{4}\right)^{16}\)
P(X ≥ 1) = P(X = 1) + P(X = 2) + ……………. + P(X = 16)
= 1 – P(X = 0)
We have P(X = r) = \({ }^n C_r\) p^rq^n-r
= 1 – \({ }^{16} \mathrm{C}_0\left(\frac{1}{4}\right)^0\left(\frac{3}{4}\right)^{16-0}\)
= 1 – 1. 1 . \(\left(\frac{3}{4}\right)^{16}\)
= 1 – \(\left(\frac{3}{4}\right)^{16}\).

Question 4.
The probability that a person choosen at random is left handed (in hand writing) is 0.1. What is the probability that in a group of 10 people, there is one who is left handed? [TS – Mar. ’16, AP – Mar. ’17, ’15; May ’12]
Solution:
Solution:
X follows binomial distribution.
Given that, the probability that a person choosen at random Is left handed
p = 0.1
q = 1 – p
= 1 – 0.1 = 0.9
n = 10, r = 1
The probability of one who is left handed = P(X = 1)
We have, P(X = r) = \({ }^n C_r\) p^rq^n-r
P(X = 1) = \(\)
= 10 . \(\frac{1}{10}\) . (0.9)⁹

Question 5.
One in 9 ships is likely to be wrecked, when they are set on sail, when 6 ships are on sail, find the probability for
i) Atleast one will arrive safely
ii) Exactly three will arrive safely. [March ’08]
Solution:
Since, one in 9 ships is likely to be wrecked.
The probability that a ship will be wrecked, q = \(\frac{1}{9}\)
P = 1 – q
= 1 – \(\frac{1}{9}\) = \(\frac{8}{9}\)
Let X be no. of ships arrive safely in the 6 ships which set on sail.
Now, X follows binomial distribution with parameters
n = 6, p = \(\frac{8}{9}\), q = \(\frac{1}{9}\)
i) The probability for atleast one will arrive safety
= P(X ≥ 1)
= P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P (X = 5) + P (X = 6)
= 1 – P (X = 0)
We have,
P(X = 6) = \({ }^n C_r\) p^rq^n-r
= 1 – \({ }^6 c_0\left(\frac{8}{9}\right)^0\left(\frac{1}{9}\right)^{6-0}\)
= 1 – 1 . 1 . \(\left(\frac{1}{9}\right)^6\)
= 1 – \(\frac{1}{9^6}\)

ii) The probability for exactly three will arrive safely = P(X = 3)
P(X = r) = \({ }^n C_r\) p^rq^n-r
= \({ }^6 \mathrm{C}_3\left(\frac{8}{9}\right)^3\left(\frac{1}{9}\right)^{6-3}\)
= \(\frac{6 \cdot 5 \cdot 4}{1 \cdot 2 \cdot 3} \cdot \frac{8^3}{9^3} \cdot \frac{1}{9^3}\)
= \(\frac{20 \cdot 512}{9^6}=\frac{10240}{9^6}\).

Question 6.
If the mean and variance of a binomial variable X are 2.4 and 1.44 respectIvely, find P(1 < x ≤ 4) [AP – Mar.’18; TS – May ’15]
Solution:
X follows binomial distribution.
In binomial distribution,
Mean = 2.4
np = 2.4 ………….(1)
Variance = 1.44
npq = 144 …………..(2)
Now,

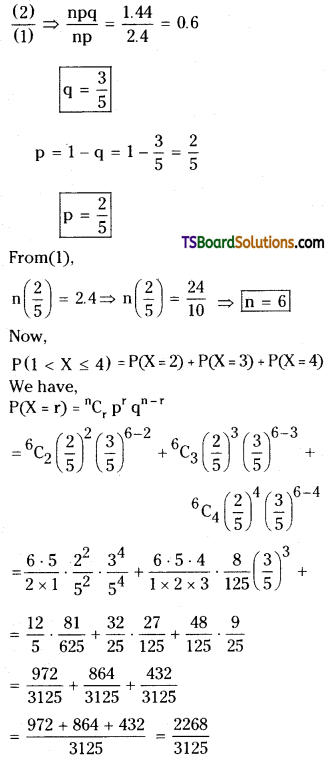
Question 7.
On an average, rain falls on 12 days in every 30 days, find the probability that, rain will fall on just 3 days of a given week.
Solution:
X follows binomial distribution.
Given that, the probability for the day to be raining
p = \(\frac{12}{30}=\frac{2}{5}\)
q = 1 – p = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
n = 7, r = 3
The probability that rain will fall on just 3 days of a given week
P(X = 3) =?
We have P(X = r) = \({ }^n C_r\) p^r q^n-r
P(X = 3) = \({ }^7 C_3\left(\frac{2}{5}\right)^3\left(\frac{3}{5}\right)^{7-3}\)
= \(\frac{7 \cdot 6 \cdot 5}{1 \cdot 2 \cdot 3} \cdot \frac{2^3}{5^3} \cdot \frac{3^4}{5^4}\)
= 35. \(\frac{2^3 \cdot 3^4}{5^7}\).

Question 8.
For a binomial distribution with mean 6 and variance 2, find the first two terms of the distribution.
Solution:
X follows binomial distribution.
In binomial distribution,
mean = 6
np = 6 ……………..(1)
variance 2
npq = 2 ……………(2)
Now,
\(\frac{(2)}{(1)} \Rightarrow \frac{n p q}{n p}=\frac{2}{6}\)
q = \(\frac{1}{3}\)
p = 1 – q
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
From (1),
n(\(\frac{2}{3}\)) = 6
The first two terms of the binomial distribution are P(X = 0) and P(X = 1).
We have P(X = r) = \({ }^n C_r\) p^r q^n-r
i) P(X = o) = \({ }^9 C_0\left(\frac{2}{3}\right)^0\left(\frac{1}{3}\right)^{9-0}\)
= 1 . 1 . \(\frac{1}{3^9}\) = \(\frac{1}{3^9}\)

ii) P(X = 1) = \({ }^9 C_1\left(\frac{2}{3}\right)^1\left(\frac{1}{3}\right)^{9-1}\)
= 9 . \(\frac{2}{3} \cdot \frac{1}{3^8}=\frac{2}{3^7}\)

Question 9.
Define Poisson distribution. [May ‘07]
Solution:
Poisson distribution:
Let λ > 0 be a real number. A random vari able, X with range {O, 1, 2, …………..} is said to follow (have) Poisson distribution with parameter λ if
P(X = r) = \(\frac{\mathrm{e}^{-\lambda} \lambda^{\mathrm{r}}}{\mathrm{r} !}\) for r = 0, 1, 2, ……………….

Question 10.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5). [Mar. ‘14, ‘10, May’14, 13, ’06, Board Paper, TS – Mar. ‘18; AP & TS – May ’16]
Solution:
We have,

Question 11.
In a book of 450 pages, there are 400 typographical en-ors. Assuming that the number of errors per page follow the Poisson law. Find the probability that a random sample of 5 pages will contain no typographical error.
Solution:
The average no. of errors for page in the book is λ = \(\frac{400}{450}=\frac{8}{9}\)
Let, X be the no. of typographical errors in a page.
Assume that X follows Poisson distribution with parameter, λ = 0.2
Now, P(X = r) = \(\frac{e^{-\lambda} \lambda^r}{r !}\)
The probability that there are no errors for a page = P(X = 0)
= \(\frac{\mathrm{e}^{-8 / 9}\left(\frac{8}{9}\right)^0}{0 !}=\mathrm{e}^{-8 / 9}\)
The required probability that a random sample of 5 pages will contain no error
= P(X = 0) . P(X = 0) . P(X = 0) . P(X = 0) . P(X = 0)
= [P(X = 0)]⁵
= \(\left[\mathrm{e}^{-8 / 9}\right]^5\)

Question 12.
In a city 10 accidents take place in a span of 50 days. Assuming that the number of accidents for the Poisson distribution, find the probability that there will 5e 3 or more accidents In a day.
Solution:
X follows Poisson distribution.
Average of accidents take place for a day.
λ = \(\frac{10}{50}=\frac{1}{5}\) = 0.2
Let, X be the no. of accidents in a day.
Assume that X follows Poisson distribution with parameter λ = 0.2.
Now,
P(X = r) = \(\frac{e^{-\lambda} \lambda^r}{r !}\) for r = 0, 1, 2, …………
The probability of 3 or more accidents in a day = P (X ≥ 3)
P (X = 3) + P(X = 4) + …………………
= 1 – [P(X = 0) + P(X = 1) + P(X = 2)]
= 1 – \(\left[\frac{\mathrm{e}^{-0.2}(0.2)^0}{0 !}+\frac{\mathrm{e}^{-0.2}(0.2)^1}{1 !}+\frac{\mathrm{e}^{-0.2}}{} \frac{0.2)^2}{}\right]\)
= 1 – e^-0.2 \(\left[1+\frac{0.2}{1}+\frac{0.04}{2}\right]\)
= 1 – e^-0.2 [1 + 0.2 + 0.02]
= 1 – e^-0.2 (1.22)