TS Inter Second Year Maths 2A Random Variables and Probability Distributions Important Questions Long Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Random Variables and Probability Distributions Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Random Variables and Probability Distributions Important Questions Long Answer Type

Question 1.
The probability distribution of a random variable X is given below:

Find the value of k and the mean and variance of X. [AP – Mar. 2019, AP- Mar. 2017: May ‘14, ’13, May ’14, ’12, ’10].
Solution:
Given that

is the probability distribution of a random variable X.
i) We know that,
\(\) P(X = x_r) = 1
i.e., Sum of probabilities = 1
P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)+ P(X = 5) = 1
k + 2k + 3k + 4k + 5k = 1
15k = 1
k = \(\frac{1}{15}\)

ii) Mean of X is
μ = \(\sum_{r=1}^5\) P(X = x_r) x_r
= 1 (k) + 2 (2k) + 3 (3k) + (4k) 4 + (5k) 5
= k + 4k + 9k + 16k + 25k = 55 k
= 55(\(\frac{1}{15}\)) = \(\frac{11}{3}\)

iii) Variance of X is
σ² = \(\sum_{r=1}^5\) P(X = x_r) x_r² – μ²
= k(1)² + 2k(2)² + 3k(3)² + 4k (4)² + 5k (5)² – (\(\frac{11}{3}\))²
= k(1) + 2k(4) + 3k(9) + 4k(16) + 5k(25) – \(\frac{121}{9}\)
= k + 8k + 27k + 64k + 125k – \(\frac{121}{9}\)
= 225k – \(\frac{121}{9}\)
= 225 (\(\frac{1}{15}\)) – \(\frac{121}{9}\)
= 15 – \(\frac{121}{9}\)
= \(\frac{135-121}{9}=\frac{14}{9}\).

Question 2.

is the probability distribution of a random variable X. find the value of k and the variance of X.
Solution:

is the probability distribution of a random variable X.
We know that,
\(\sum_{r=-2}^3\) P(X = x_r) = 1
i.e., Sum of probabilities = 1
P(X = – 2) + P(X = – 1) + P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 1
0.1 + k + 0.2 + 2k + 0.3 + k = 1
4k + 0.6 = 1
4k = 1 – 0.6
4k = 0.4
k = 0.1
k = \(\frac{1}{10}\)
Mean of X is μ = \(\sum_{r=-2}^3\) (X = x_r) . x_r
= (- 2) (0.1) + (- 1) k + 0(0.2) + 1(2k) + 2(0.3) + 3k
= – 0.2 – k + 0 + 2k + 0.6 + 3k
= 0.4 + 4k
= 0.4 + 4 (\(\frac{1}{10}\))
= 0.4 + 0.4 = 0.8
= \(\frac{8}{10}=\frac{4}{5}\)
Variance of X is σ² = \(\sum_{r=1}^5\) P(X = x_r) x_r² – μ²
= (- 2)² (0.1) + k(- 1)² + (0.2) (0)² + 2k(1)² 0.3(2)² + k(3)² – (\(\frac{4}{5}\))²
= 4 . (0.1) + k . 1 + 0.2 (0) + 2k . 1 + 0.3(4) + k . 9 – \(\frac{16}{25}\)
= 0.4 + k + 0 + 2k + 1.2 + 9k – \(\frac{16}{25}\)
= 1.6 + 12k – \(\frac{16}{25}\)
= \(\frac{16}{10}+\frac{12}{10}-\frac{16}{25}\)
= \(\frac{160+120-64}{100}=\frac{216}{100}\) = 2.16.

Question 3.
A random variable X has the following probability distribution.

Find i) k
ii) the mean and
iii) P(0 < X < 5). [May ’12, ’10, ’08, March ‘09, Board Paper] [AP – May, Mar.16; TS – Mar. ‘18, ‘16]
Solution:

is the probability distribution function.
i) We know that,
\(\sum_{\mathbf{r}=0}^7\) P(X = x) = 1
i.e., Sum of the probabilities = 1
P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7)=
0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
10k² + 9k – 1 = 0
10k² + 10k – k – 1 = 0
10k (k + 1) – 1(k + 1) = 0
(k + 1) (10k – 1) = 0
k + 1 = 0 (or) 10k – 1 = 0
k = – 1 (or) k = \(\frac{1}{10}\)
k = – 1 does not satisfy the given probabilities.
∴ k = \(\frac{1}{10}\).

ii) The mean of X is
μ = \(\sum_{r=0}^7\) (X = x_r) . x_r
= 0 . 0 + 1(k) + 2(2k) + 3(2k) + 4(3k)+ 5(k²) + 6(2k²) + 7 (7k² + k)
= 0 + k + 4k + 6k + 12k + 5k² + 12k² + 49k² + 7k
= 66k² + 30k
= \(66\left(\frac{1}{10}\right)^2+30\left(\frac{1}{10}\right)\)
= \(\frac{66}{100}+\frac{30}{10}\)
= 0.66 + 3 = 3.66.

iii) P(0 < X < 5)
= P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k = 8(\(\frac{1}{10}\))
= 0.8 = \(\frac{4}{5}\).

Question 4.
The range of a random variable X is {0, 1, 2}. Given that P(X= 0) = 3c³, P(X = 1) = 4c – 10c², P(X = 2) = 5c – 1. Find
(i) the value of c
(ii) P(X < 1),
(iii) P (1 < X ≤ 2) and P (0 < X ≤ 3). [March ‘13. ‘11, ‘07. ‘05, ‘95; May ‘11. 09. ‘91, TS – Mar. 2015; AP – Mar. 2015]
Solution:
The range of a random variable, X is {O, 1, 2}
Given that,
P(X = 0) = 3c³, P(X = 1) = 4c – 10c²,
P(X = 2) = 5c – 1
ï) We know that,
\(\sum_{\mathrm{r}=0}^2\) P(X = x_r) = 1
i.e., Sum of the probabilities = 1
P(X = 0) + P(X = 1) + P(X = 2) = 1
3c³ + 4c – 10c² + 5c – 1 = 1
3c³ – 10c² + 9c – 2 = 0
Let, f(c) = 3c³ – 10c² + 9c – 2
If c = 1 then,
f(1) = 3(1)³ – 10(1)² + 9(1) – 2
1(1) = 3 – 10 + 9 – 2
= 12 – 12 = 0
∴ c = 1 is a root of 1(c) = 0

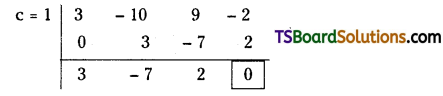
3c² – 7c + 2 = 0
3c² – 6c – c + 2 = 0
3c (c – 2) – 1(c – 2) = 0
(c – 2) (3c – 1) = 0
c – 2 = 0 (or) 3c – 1 = 0
c = 2 (or) c = \(\frac{1}{3}\)
∴ c = 1, 2, \(\frac{1}{3}\)
c = 1, 2 does not satisfy the given probabilities.
∴ c = \(\frac{1}{3}\)

ii) P(X < 1) = P(X = 0)
= 3c³
= 3(\(\frac{1}{3}\))³
= \(\frac{3}{27}=\frac{1}{9}\)

iii) P(1 < X ≤ 2)
= P(X = 2)
= 5c – 1
= 5 . \(\frac{1}{3}\) – 1
= \(\frac{5-3}{3}=\frac{2}{3}\)

iv)P(0 < X < 3) = P(X = 1) + P(X = 2)
= 4c – 10c² + 5c – 1
= 9c – 10c² – 1
= 9(\(\frac{1}{3}\)) – 10(\(\frac{1}{9}\)) – 1
= \(\frac{27-10-9}{9}=\frac{8}{9}\).

Question 5.
The range of a random variable X is {1, 2, 3, …………..} and P(X = k) = (k = 1, 2, 3, ………………). Find the value of c and P(0 < X < 3). [TS – May 2015; March 2003, May 2009]
Solution:
The range of a random variable, X is {1, 2, 3, …………..}.
Given that,
P(X = k) = \(\) k = 1, 2, 3 …………….
i) We know that,
\(\) P(X = x_k) = 1
i.e, sum of the probabilities = 1
P(X = 1) + P(X = 2) + P(X = 3) + …………………. = 1
\(\frac{\mathrm{c}}{1 !}+\frac{\mathrm{c}^2}{2 !}+\frac{\mathrm{c}^3}{3 !}+\ldots \ldots\)
\(e^x=1+\frac{x}{1 !}+\frac{x^2}{2 !}+\ldots \ldots\)
\(1+\frac{\mathrm{c}}{1 !}+\frac{\mathrm{c}^2}{2 !}+\frac{\mathrm{c}^3}{3 !}+\ldots \ldots\)
e^c = 2.
c = log_e 2

ii) P(0 < X < 3)
= P(X = 1) + P(X = 2)
= \(\frac{c}{1 !}+\frac{c^2}{2 !}=\frac{c}{1}+\frac{c^2}{2}\)
= log_e 2 + \(\frac{\left(\log _{\mathrm{e}} 2\right)^2}{2}\).

Question 6.
A cubical die is thrown. Find the mean and variance of X, giving the number on the face that shows up. [TS – Mar. 2019] [TS – May 2016; AP – May’ 2015]
Solution:
Let S be the sample space and X be the random variable associated with S, where P(X) is given by the following table.

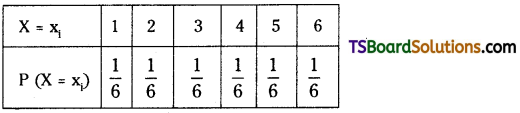
Mean of X is μ = \(\sum_{r=1}^6\) P(X = x_r) . x_r

Question 7.
If X is a random variable with probability distribution P(X = k) = \(\frac{(k+1) c}{2^k}\), k = 0, 1, 2, …………….. then find c. AP – Mar. 2018;
Solution:
Given that,
P(X = k) = \(\frac{(k+1) c}{2^k}\), k = 0, 1, 2, ………………. is the probability distribution of X.
We know that,
\(\sum_{k=0}^{\infty}\) P(X = x_k) = 1
i.e., sum of the probabilities = 1
P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + ………………. = 1
\(\frac{1 \cdot c}{2^0}+\frac{2 \cdot c}{2}+\frac{3 \cdot c}{2^2}+\frac{4 \cdot c}{2^3}+\ldots \ldots\) = 1

Question 8.
Let X be a random variable such that P(X = – 2) = P(X = – 1) = P(X = 2) = P(X = 1) = \(\frac{1}{6}\) and P(X = 0) = \(\frac{1}{3}\). Find the mean and variance of X.
Solution:
X is a random variable.
Given that, P(X = – 2) = \(\frac{1}{6}\)
P(X = – 1) = \(\frac{1}{6}\)
P(X = 2) = \(\frac{1}{6}\)
P(X = 1)= \(\frac{1}{6}\)
P (X = 0) = \(\frac{1}{6}\)

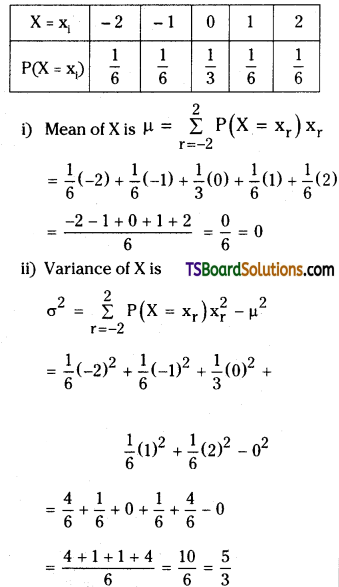
Question 9.
Two dice are rolled at random. Find the probability distribution of the sum of the numbers on them. Find the mean of the random variable.
Solution:
When two dice are rolled, the sample space S’ consists of 6 × 6 = 36.
Sample points are
S = {(1, 1), (1, 2), (1, 3), (1,4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), 4, 3), (4, 4), (4. 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5,4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6))
Let X denote the sum of the numbers on the two dice.
Then the range of X is {2, 3, 4, 5, 6, …………………, 12)
The probability distribution for X is given here under:

Question 10.
Find the constant ‘c’, so that F(x) = c \(\left(\frac{2}{3}\right)^x\) x = 1, 2, 3, …….. is the p.d.f. of a discrete random variable X.
Solution:
Given that,
F(x) = c \(\left(\frac{2}{3}\right)^x\), x = 1, 2,3,….. is the probability distribution function.
We know that,
\(\sum_{r=1}^{\infty}\) P(X = x_r) = 1
i.e., sum of the probabilities = 1
P(X = 1) + P(X = 2) + P(X = 3) + …………. = 1
\(c\left(\frac{2}{3}\right)^1+c\left(\frac{2}{3}\right)^2+c\left(\frac{2}{3}\right)^3+\ldots \ldots \ldots\) = 1
\(c\left[\frac{2}{3}+\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\ldots \ldots\right]\) = 1
Here, a = \(\frac{2}{3}\), r = \(\frac{2}{3}\)
S_∞ = \(\frac{a}{1-r}\)
c\(\left[\frac{\frac{2}{3}}{1-\frac{2}{3}}\right]\) = 1
\(c\left[\frac{\frac{2}{3}}{\frac{1}{3}}\right]\) = 1
c(2) = 1
c = \(\frac{1}{2}\).

Question 11.
In the experiment of tossing a coin n times, if the variable X denotes the number of heads ndP(X=4),P(X=5),P(X=6) are in arithmetic progression then find n. [March 2002]
Solution:
X follows binomial distribution with p = \(\frac{1}{2}\), q = \(\frac{1}{2}\)
Given that,
P(X = 4), P(X = 5), P(X = 6) are in A.P.
Since a, b, c are in A.P. then
∴ 2P(X = 5) = P(X = 4) + P(X = 6)
We have,
P(X = r) = \({ }^n \mathrm{C}_1\) p^rq^1-r

12 (n – 4) = 30 + (n – 5) (n – 4)
12n – 48 = 30 + n² – 9n + 20
n² – 21n + 98 = 0
n² – 14n – 7n + 98 = 0
n (n – 14) – 7(n – 14) = 0
(n – 14) (n – 7) = 0
n – 14 = 0 (or) n – 7 = 0
n = 14 (or) n = 7
∴ n = 7 (or) 14.