TS Inter Second Year Maths 2A Complex Numbers Important Questions Short Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Complex Numbers Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Complex Numbers Important Questions Short Answer Type

Question 1.
Determine the locus of z, z ≠ 2i, such that Re (\(\frac{z-4}{z-2 i}\)) = 0.
Solution:
Let z = (x + iy)
Now,

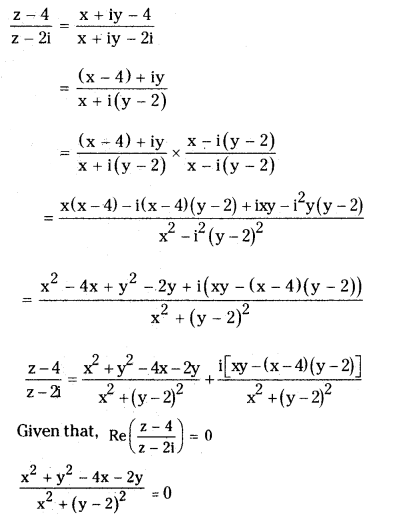
x² + y² – 4x – 2y = 0
x² + 4 – 4x – 4 + y² – 2y + 1 – 1 = 0
(x – 2)² + (y – 1)² = 5
∴ The locus of z is (x – 2)² + (y – 1)² = 5
The locus represents a circle with centre (2, 1) and radius √5 units.

Question 2.
Show that \(\frac{2-i}{(1-2 i)^2}\) and \(\frac{-2-11}{25}\) conjugate to each other. [May ’97]
Solution:
Let the given complex number are
z₁ = \(\frac{2-\mathrm{i}}{(1-2 \mathrm{i})^2}\) and z₂ = \(\frac{-2-11 i}{25}\)

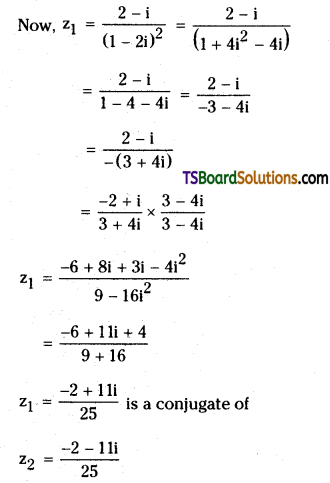
∴ z₁ and z₂ are conjuagte to each other.

Question 3.
If x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) then, show that x² + y² = 4x – 3.
Solution.

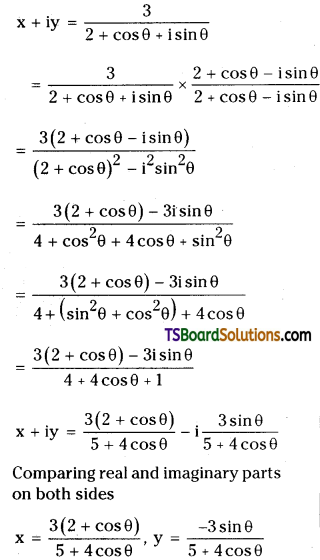
L.H.S:

From (1) and (2);
L.H.S = R.H.S
x² + y² = 4x – 3.

Question 4.
If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\) then, show that 4x² – 1 = 0.
[March ’06, May ‘82, TS- Mar. ‘15, May ’16; AP- May, Mar. 2016, AP & TS – Mar. 2019]
Solution:

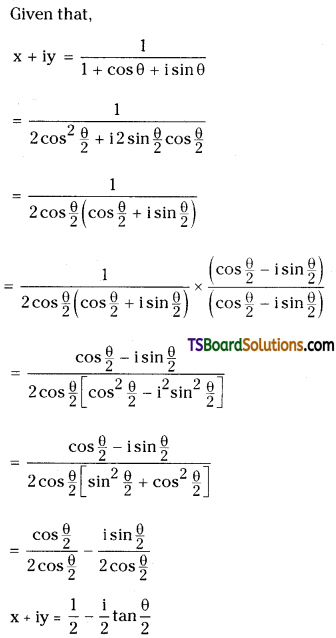
Comparing real parts on both sides
x = \(\frac{1}{2}\)
x² = \(\frac{1}{4}\)
4x² = 1
∴ 4x – 1 = 0

Question 5.
If u + iv = \(\frac{2+i}{z+3}\) and z = x + iy, find u, v. [March ’81]
Solution:

Question 6.
If z = 2 – i√7 then show that 3z³ – 4z² + z + 88 = 0. [March 2000]
Solution:
Given that,
z = 2 – i√7
Now,
z² = (2 – i√7)²
= 4 + i² 7 – 4√7i
= 4 – 7 – 4√7i
= – 3 – 4√7i

L.H.S:
3z³ – 4z² + z + 88 = 3z² . z – 4z² + z + 88
= 3 (- 3 – 4i√7) (2 – i√7) – 4(- 3 – 4√7) + (2 – i√7) + 88
= – 18 + 9√7i – 24√7i + 84i² + 12 + 16√7i + 2 -i√7 + 88
= – 18 – 84 + 12 + 2 + 88 = 0 = R.H.S
∴ 3z³ – 4z² + z + 88 = 0.

Question 7.
If (x – iy)^1/3 = a – ib then show that \(\) = 4(a² – b²). (Ap-Mar 2018)
Solution:
Given that
(x – iy)^1/3 = a – ib
Cubing on both sides,
[(x – iy)^1/3]³ = (a – ib)³
x – iy = a³ – i³b³ – 3iab (a – ib)
x – iy = a³ – i² . ib³ – 3 ia²b + 3i²ab²
x – iy = a³ – 3ab² + ib³ – 3ia²b
x – iy = a (a² – 3b²) + ib (b² – 3a²)
Comparing real and imaginary parts on both sides
x = a(a² – 3b²)
\(\frac{x}{a}\) = a² – 3b² ……………(1)

– y = b(b² – 3a²)
\(-\frac{y}{b}\) = – (3a² – b²)
\(\frac{y}{b}\) = 3a² – b² …………..(2)
Now. (1) + (2)
\(\frac{x}{a}\) + \(\frac{y}{b}\) = a² – 3b² + 3a² – b²
∴ \(\frac{x}{a}\) + \(\frac{y}{b}\) = 4 (a² – b²)

Question 8.
Write \(\left(\frac{a+i b}{a-i b}\right)^2-\left(\frac{a-i b}{a+i b}\right)^2\) in the form x + iy.
Solution:
Given that,

Question 9.
If x and y are real numbers such that \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-i}\) = i then determine the values of x and y.
Solution:
\(\frac{(1+\mathrm{i}) \mathrm{x}-2 \mathrm{i}}{3+\mathrm{i}}+\frac{(2-3 \mathrm{i}) \mathrm{y}+\mathrm{i}}{3-\mathrm{i}}\) = i

i = \(\frac{[(1+\mathrm{i}) \mathrm{x}-2 \mathrm{i}](3-\mathrm{i})+[(2-3 \mathrm{i}) \mathrm{y}+\mathrm{i}](3+\mathrm{i})}{(3+\mathrm{i})(3-\mathrm{i})}\)

i = \(\frac{(2-3 i) 3 y+3 i+(2-3 i) i y+i^2}{\left(9-i^2\right)}\)
10i = (3x + 3ix – 6i – xi – xi² – 2) + 6y – 9iy + 3i + 2iy – 3i²y – 1
(3x + x – 2 + 6y + 3y – 1) + i(3x – 6 – x – 9y + 3 + 2y) = 10i
(4x + 9y – 3) + i(2x – 7y – 3) = 10i + 0
Comparing real and imaginary parts on both sides
4x + 9y – 3 = 0 …………..(1)
2x – 7y – 3 = 10
2x – 7y – 3 = 10 ………….(2)
From (1) and (2);

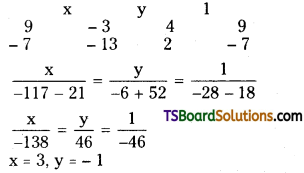
Question 10.
If \(\left(\frac{1+i}{1-i}\right)^3-\left(\frac{1-i}{1+i}\right)^3\) = x + iy find x and y.
Solution:
Given that,

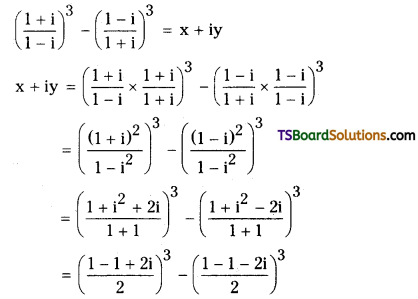
x + iy = i³ + i³
2i³ = x + iy
2i²(i) = x + iy
2(- 1)i = x + iy
0 + i(- 2) = x + iy
Comparing real and imaginary parts on both sides
x = 0, y = – 2.

Question 11.
Find the real values of θ in order that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is a
a) real number
b) purely imaginary number.
Solution.

a) If z is a real number
⇒ Imaginary part of z = 0
⇒ \(\frac{8 \sin \theta}{1+4 \sin ^2 \theta}\) = 0
8 sin θ = 0
sin θ = 0
∴ θ = nπ, n ∈ Z

b) If z ¡s purely imaginary
⇒ Real part of z = 0
⇒ \(\frac{3-4 \sin ^2 \theta}{1+4 \sin ^2 \theta}\) = 0
3 – 4 sin² θ = 0
sin² θ = \(\frac{3}{4}\)
sin² θ = \(\left(\frac{\sqrt{3}}{2}\right)^2\)
sin² θ = sin² \(\frac{\pi}{3}\)
∴ θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z.

Question 12.
Find the real values of x and y if \(\frac{x-1}{3+1}+\frac{y-1}{3-1}\) = i.
Solution:
Given that,
\(\frac{x-1}{3+i}+\frac{y-1}{3-i}\) = i
\(\frac{(x-1)(3-i)+(y-1)(3+i)}{(3+i)(3-i)}\) = i
\(\frac{3 x-x i-3+i+3 y+y i-3-i}{9-i^2}\) = i
3x + 3y – 6 + i(- x + y) = 10i
3x + 3y – 6 + i(- x + y) = 0 + i(10)
Comparing the real and imaginary parts on both sides
3x + 3y – 6 = 0 ………….(1)
y – x = 10
x – y + 10 = 0 …………..(2)
From (1) and (2)

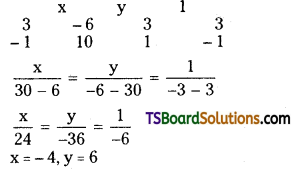
Question 13.
If the amplitude of \(\left[\frac{z-2}{z-6 i}\right]=\frac{\pi}{2}\), find its locus. [May ‘06]
Solution:
Let, z = x + iy
Now,

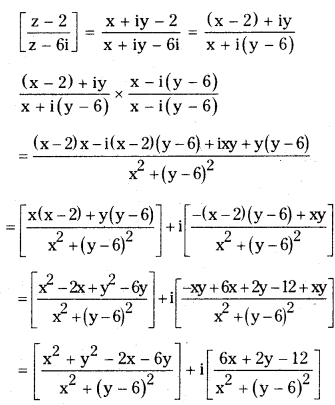
Given that,
the amplitude of \(\left[\frac{z-2}{z-6 i}\right]=\frac{\pi}{2}\) then,
tan^-1 \(\left[\frac{\frac{6 x+2 y-12}{x^2+(y-6)^2}}{\frac{x^2+y^2-2 x-6 y}{x^2+(y-6)^2}}\right]=\frac{\pi}{2}\)
\(\frac{6 x+2 y-12}{x^2+y^2-2 x-6 y}\) = tan \(\frac{\pi}{2}\) = ∞ = \(\frac{1}{0}\)
x² + y² – 2x – 6y = 0
∴ Locus of z is x² + y² – 2x – 6y = 0.

Question 14.
If the point P denotes the complex number z = x + iy in the Argand plane and if \(\frac{z-i}{z-1}\) is a purely imaginary number, find the locus of P. [March 06, May 08 (old)] [AP-Mar.2017]
Solution:
Given, z = x + iy
⇒ P = (x, y)

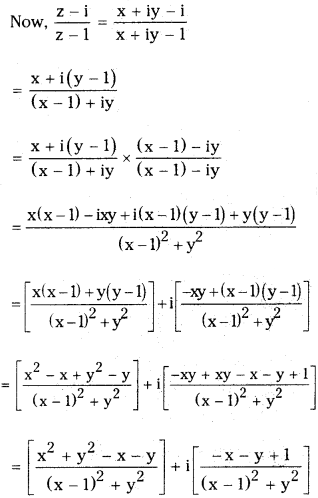
Given that,
\(\frac{z-i}{z-1}\) is a purely imaginary then real part = 0
\(\frac{x^2+y^2-x-y}{(x-1)^2+y^2}\) = 0
x² + y² – x – y = 0
∴ Locus of P is x² + y² – x – y = 0.

Question 15.
If z = x + iy and if the point P in the Argand plane represents z, then describe geometrically the locus of z satisfying the equation |z – 2 – 3i| = 5. [Board Paper]
Solution:
Given, z = x + iy
⇒ P (x, y)
|z – 2 – 3i| = 5
|x + iy – 2 – 3i| = 5
|(x – 2) + i (y – 3)| = 5
\(\sqrt{(x-2)^2+(y-3)^2}\) = 5
Squaring on both sides
(x – 2)² + (y – 3)² = 25
x² – 4x + 4 + y² + 9 – 6y – 25 = 0
x² + y² – 4x – 6y – 12 = 0
∴ Locus of P is x² + y² – 4x – 6y – 12 = 0
Locus represents a circle with centre (2, 3) and radius 5 units.

Question 16.
Show that the points in the Argand plane represented by the complex numbers -2 + 7i, \(\frac{-3}{2}\) + \(\frac{1}{2}\) i, 4 – 3i, \(\frac{7}{2}\) (1 + i) are the vertices of a rhombus. [AP – Mar. 2015] [TS – Mar. 2016; March’05, ‘05, ‘04, 2000]
Solution:
Let, the given points are
A = – 2 + 7i, B = \(\frac{-3}{2}+\frac{1}{2} \mathrm{i}\)
C = 4 – 3i, D = \(\frac{7}{2}\) (1 + i)
A = – 2 + 7i = (- 2, 7)
B = \(\frac{-3}{2}+\frac{1}{2} \mathrm{i}=\left(\frac{-3}{2}, \frac{1}{2}\right)\)
C = 4 – 3i = (4, – 3)
D = \(\frac{7}{2}\) (1 + i) = \(\left(\frac{7}{2}, \frac{7}{2}\right)\)

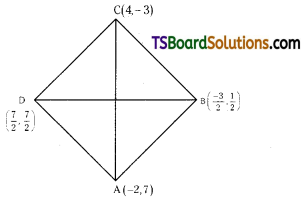
∴ AB = BC = CD = DA and AC ≠ BD
∴ The given points form a rhombus.

Question 17.
The points P, Q denote the complex numbers z₁, z₂ in the Argand diagram. O is the origin. If z₁\(\overline{\mathbf{z}}_2\) + \(\overline{\mathbf{z}}_1\)z₂ = 0, then show that ∠POQ = 90° [March 07]
Solution:
Given points P, Q denote the complex numbers z₁, z₂.
Let z₁ = x₁ + iy₁
⇒ P (x₁, y₁)
\(\overline{\mathrm{Z}}_1\) = x₁ – iy₁
⇒ Q (x₂, y₂)
z₂ = x₂ + iy₂

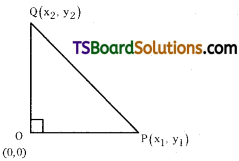
Since, z1\(\overline{\mathrm{Z}}_2\) + \(\overline{\mathrm{Z}}_1\)z₂ = 0
(x₁ + iy₁) (x₂ – iy₂) + (x₁ – iy₁) (x₂ + iy₂) = 0
x₁x₂ – ix₁y₂ + ix₂y₁ + y₁y₂ + x₁x₂ + ix₁y₂ – ix₂y₁ + y₁y₂ = 0
2(x₁x₂ + y₁y₂) = 0
x₁x₂ + y₁y₂ = 0
x₁x₂ = – y₁y₂
\(\frac{\mathrm{y}_1 \mathrm{y}_2}{\mathrm{x}_1 \mathrm{x}_2}\) = – 1
\(\left(\frac{\mathrm{y}_1}{\mathrm{x}_1}\right)\left(\frac{\mathrm{y}_2}{\mathrm{x}_2}\right)\) = – 1
Slope of \(\overline{\mathrm{OP}}\) × Slope of \(\overline{\mathrm{OQ}}\) = – 1
∴ ∠POQ = 90°

Some More Maths 2A Complex Numbers Important Questions

Question 1.
Find the multiplicative inverse of (3, 4).
Solution:
Let z = (3, 4)
The multiplicative inverse of z is
\(\mathrm{z}^{-1}=\frac{1}{\mathrm{z}}=\left(\frac{\mathrm{a}}{\mathrm{a}^2+\mathrm{b}^2}, \frac{-\mathrm{b}}{\mathrm{a}^2+\mathrm{b}^2}\right)\)

\(z^{-1}=\left(\frac{3}{3^2+4^2}, \frac{-4}{3^2+4^2}\right)\)

= \(\left(\frac{3}{9+16}, \frac{-4}{9+16}\right)=\left(\frac{3}{25}, \frac{-4}{25}\right)\)

Question 2.
Write \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\) in the form a + ib.
Solution:

Question 3.
Write the complex number (1 + 2i)³ in the form a + ib.
Solution:
Let z = (1 + 2i)³
= 1³ + (2i)³ + 3(1) (2i)² + 3(1)² (2i)
= 1 + 8i³ + 12i² + 6i
=1 + 8i²(i) + 6i – 12
= 1 – 81 + 6i – 12
= – 11 – 2i
= – 11 + i(- 2)
It is in the form a + ib.

Question 4.
Find the multiplicative inverse of √5 + 3i.
Solution:
Let z = √5 + 3i
The multiplicative inverse of z is
\(z^{-1}=\frac{1}{z}=\frac{1}{\sqrt{5}+3 i}\)
= \(\frac{1}{\sqrt{5}+3 \mathrm{i}} \times \frac{\sqrt{5}-3 \mathrm{i}}{\sqrt{5}-3 \mathrm{i}}\)
= \(\frac{\sqrt{5}-3 \mathrm{i}}{5-9 \mathrm{i}^2}=\frac{\sqrt{5}-3 \mathrm{i}}{5+9}=\frac{\sqrt{5}-3 \mathrm{i}}{14}\)

Question 5.
Write the conjugate of (2 + 5i) (- 4 + 6i).
Solution:
Let z = (25i) (- 4 + 6i)
z = – 8+ 12i – 20i + 30i²
z = – 8 – 8i – 30
z = – 38 – 8i
The conjugate of z is \(\bar{z}=(\overline{-38-8 i})\) = -38 + 81

Question 6.
Find the square roots of 3 + 4i.
Solution:
Let \(\sqrt{3+4 i}\) = ± (x + iy)

Question 7.
Find the square roots of 7 + 24i.
Solution:
Let \(\sqrt{7+24 i}\) = ± (x + iy)

Question 8.
Find the square roots of – 8 – 6i.
Solution:
Let \(\sqrt{-8-6 i}\) = ± (x – iy)

Question 9.
Show that z₁ = \(\frac{2+11 i}{25}\), z₂ = \(\frac{-2+i}{(1-2 i)^2}\) are conjugate to each other.
Solution:
Given that,

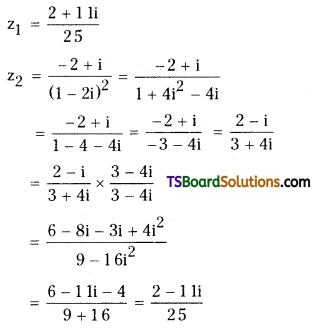
Since, this complex number is conjugate of \(\frac{2+11 i}{25}\).
∴ z₁ and z₂ are conjugate to each other.

Question 10.
If z = 3 – 5i then show that z³ – 10z² + 58z – 136 = 0.
Solution:
Given that, z = 3 – 5
Now, z² = (3 – 5i)² = 9 + 25i² – 30i
= 9 – 25 – 30i = – 16 – 30i
L.H.S:
z³ – 10z² + 58z – 136 = z²z – 10z² + 58z – 136
= (- 16 – 30i) (3 – 5i) – 10 (- 16 – 30i)+ 58 (3 – 5i) – 136
= – 48 + 80i – 90i + 150i² + 160 + 300i + 174 – 290i – 136
= – 48 – 150 + 160 + 174 – 136 = 0 = R.H.S.
∴ z³ – 10z² + 58z – 136 = 0.

Question 11.
If z₁ = (3, 5) and z₂ = (2, 6) find z₁ z₂.
Solution:
Given that,
z₁ = (3, 5), z₂ = (2, 6)
z₁ z₂ = (3, 5) . (2, 6)
= (3.2 – 5.6, 3.6 + 2.5)
= (6-30, 18 + 10)
= (- 24, 28)

Question 12.
Write the additive Inverse of (- 6, 5) + (10, – 4).
Solution:
Let,
z = (- 6, 5) + (10, – 4)
= (- 6 + 10, 5 – 4)
= (4, 1)
∴ The additive inverse of z is
– z = – (4, 1) = (- 4, – 1).

Question 13.
Write the additive inverse of (2, 1) (- 4, 6).
Solution:
Let,
z = (2, 1) (- 4, 6)
= (2 . (- 4) – 1 . 6, 2 . 6 + 1 . (- 4))
= (- 8 – 6, 12 – 4)
= (- 14, 8)
∴ The additive inverse of z is
– z = – (- 14, 8) = (14, – 8).

Question 14.
If z₁ = (6, 3), z₂ = (2, – 1) find \(\frac{z_1}{z_2}\).
Solution:
Given that,
z₁ = (6, 3), z₂ = (2, – 1)
\(\frac{z_1}{z_2}=\frac{(6,3)}{(2,-1)}=\left(\frac{6 \cdot 2+3 \cdot-1}{2^2+(-1)^2}, \frac{3 \cdot 2-6 \cdot-1}{2^2+(-1)^2}\right)\)
= \(\left(\frac{12-3}{4+1}, \frac{6+6}{4+1}\right)\)
= \(\left(\frac{9}{5}, \frac{12}{5}\right)\)

Question 15.
VrItethe multiplicative inverse of (7, 24).
Solution:
Let z = (7, 24)
The multiphcative inverse of z ¡s
\(z^{-1}=\left(\frac{a}{a^2+b^2}, \frac{-b}{a^2+b^2}\right)\)
= \(\left(\frac{7}{7^2+24^2}, \frac{-24}{7^2+24^2}\right)\)
= \(\left(\frac{7}{49+576}, \frac{-24}{49+576}\right)\)
= \(\left(\frac{7}{625}, \frac{-24}{625}\right)\).

Question 16.
Write the complex number (2 – 3i) (3 + 4i) in the form A + iB. [AP – Mar. 2017]
Solution:
Let z = (2 – 3i) (3 + 4i)
= 6 + 8i – 9i – 12i²
= 6 – i + 12
= 18 – i = 18 + (- 1)i
It is in the form A + iB.

Question 17.
Write the complex number \(\frac{a-i b}{a+i b}\) in the form A + iB.
Solution:

Question 18.
Write the complex number \(\frac{4+3 i}{(2+3 i)(4-3 i)}\) in the form A + iB.
Solution:

Question 19.
Write the complex number (- √3 + √-2) (2√3 – i) in the form A + iB.
Solution:
Let, z = (- √3 + √-2) (2√3 – i)
= (- √3 + √2i) (2√3 – i)
= – 6 + √3i + 2√6i – \(\sqrt{2} \mathrm{i}^2\)
= – 6 + (√3 + 2√6)i + √2
= (√2 – 6) + i(√3 + 2√6)
It is in the form A + iB.

Question 20.
Write the complex number (- 5i) (i/8) in the form A + iB.
Solution:
Let, z = (- 5i) (\(\frac{i}{8}\))
= \(\frac{-5 \mathrm{i}^2}{8}\)
= \(\frac{5}{8}\)
= \(\frac{5}{8}\) + i(0)
It is in the form A + iB.

Question 21.
Write the complex number (- i) 2i in the form A + iB.
Solution:
Let, z = (- i) (2i) = – 2i²
= 2 = 2 + i(0)
It is in the form A + iB.

Question 22.
Write the complex number i⁹ in the form A + iB.
Solution:
Let, z = i⁹ = i⁸ i = (i²)⁴ i
= (- 1)⁴ i = i = 0 + i(1)
It is in the form A + iB.

Question 23.
Write the complex number 3 (7 + 7i) + i(7 + 7i) in the form A + IB.
Solution:
Let, z = 3 (7 + 7i) + i (7 + 7i)
= 21 + 21i + 7i + 7i
= 21 + 28i – 7
= 14 + 28i
= 14 + i(28)
It is in the form A + iB.

Question 24.
Find the complex conjugate of (15 + 3i) – (4 – 20i).
Solution:
Let, z = (15 + 3i) – (4 – 20i)
= 15 + 3i – 4 + 20i
= 11 + 23i
The conjugate of z is \(\overline{\mathrm{z}}=(\overline{11+23 \mathrm{i}})\) = 11 – 23i.

Question 25.
Find the complex conjugate of \(\frac{5 i}{7+i}\).
Solution:

Question 26.
Find the multiplicative inverse of the complex number – i.
Solution:
Let, z = – i
The multiplicative inverse of z is
\(z^{-1}=\frac{1}{z}=\frac{1}{-i}=\frac{-1}{i}=\frac{i^2}{i}\) = i.

Question 27.
Find the multiplicative inverse of the complex number i^-35.
Solution:
Let, z = i^-35
The multiplicative inverse of z^-1 is
\(z^{-1}=\frac{1}{z}=\frac{1}{i^{-35}}\) = i³⁵
= i³⁴ . i
= (i²)¹⁷ i
= (- 1)¹⁷ i = – i.

Question 28.
Show that the equation of any circle in the complex plane is of the form \(\mathbf{z} \overline{\mathbf{z}}+\mathbf{b} \overline{\mathbf{z}}+\overline{\mathbf{b}} \mathbf{z}+\mathbf{c}\) = 0.
Solution:
Let the equation of a circle in cartesian coordinates ¡s
x² + y² + 2gx + 2fy + c = 0 …………….(1)
Let, z = x + iy then \(\overline{\mathrm{z}}\) = x – iy
Now, z\(\overline{\mathrm{z}}\) = (x + iy) (x – iy)
= x² + y²
z\(\overline{\mathrm{z}}\) = x² + y²
z + \(\overline{\mathrm{z}}\) = x + iy + x – iy = 2x
∴ z + \(\overline{\mathrm{z}}\) = 2x
z – \(\overline{\mathrm{z}}\) = x + iy – x + iy = 2iy
\(\frac{z-\bar{z}}{i}\) = 2y
\(\frac{z-\bar{z}}{i} \times \frac{i}{i}\) = 2y
\(\frac{\mathrm{i}(\mathrm{z}-\overline{\mathrm{z}})}{-1}\) = 2y
2y = – i (z – \(\overline{\mathrm{z}}\))
Substituting these results in (1) we obtain
z\(\overline{\mathrm{z}}\) + g(z + \(\overline{\mathrm{z}}\))+ f[- i(z – \(\overline{\mathrm{z}}\))] + c = 0
z\(\overline{\mathrm{z}}\) + gz + g\(\overline{\mathrm{z}}\) – ifz + if\(\overline{\mathrm{z}}\) + c = 0
Let g + if = b, then g – if = \(\overline{\mathrm{b}}\)
∴ z\(\overline{\mathrm{z}}\) + \(\overline{\mathrm{b}}\)z + b\(\overline{\mathrm{z}}\) + c = 0.

Question 29.
Exprese the complex iiumber 1 – i in modulus amplitude form. [AP- Mar, 2015]
Solution:

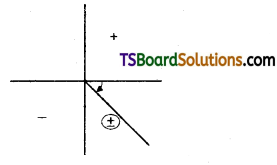
Let. 1 – i = r(cos θ + i sin θ)
then r cos θ = 1, r sin θ = – 1
r = \(\sqrt{x^2+y^2}=\sqrt{(1)^2+(-1)^2}\)
= \(\sqrt{1+1}=\sqrt{2}\)
Hence,
√2 cos θ = 1
cos θ = \(\frac{1}{\sqrt{2}}\)

√2 sin θ = – 1
sin θ = \(\frac{-1}{\sqrt{2}}\)

∴ θ lies in Q₄
∴ θ = \(\frac{-\pi}{4}\)
∴ 1 – i = √2 (cos (\(\frac{-\pi}{4}\)) + i sin (\(\frac{-\pi}{4}\)))

Question 30.
Exprcs the complex number 1 + i√3 in modulus amplitude form. [Mar. 14, TS – Mar.2017]
Solution:

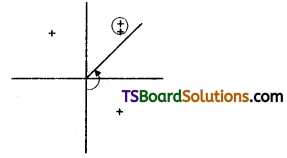
Let, 1 + i√3 = r(cos θ + i sin θ)
then r cos θ = 1, r sin θ = √3
∴ r = \(\sqrt{x^2+y^2}=\sqrt{(1)^2+(\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4}\) = 2
Hence,
2 cos θ = 1
cos θ = \(\frac{1}{2}\)

2 sin θ = √3
sin θ = \(\sqrt{3}{2}\)

∴ θ lies in Q₁
∴ θ = \(\frac{\pi}{3}\)
∴ 1 + i√3 = 2 (cos (\(\frac{\pi}{3}\)) + i sin (\(\frac{\pi}{3}\)))

Question 31.
If z ≠ 0, find Arg z + Arg \(\overline{\mathbf{z}}\).
Solution:
If z = x + iy then
Arg z = tan^-1 (\(\frac{y}{x}\))

If \(\overline{\mathbf{z}}\) = x – iy then
Arg \(\overline{\mathbf{z}}\) = tan^-1 (\(\frac{-y}{x}\))
= – tan^-1 (\(\frac{y}{x}\))
Now,
Arg z + Arg \(\overline{\mathbf{z}}\) = tan^-1 (\(\frac{y}{x}\)) – tan^-1 (\(\frac{y}{x}\)) = 0

Question 32.
If \(\frac{\mathbf{z}_2}{\mathbf{z}_1}\), 1 ≠ o, is an imaginary number then find the value of \(\left|\frac{2 z_1+z_2}{z_1-z_2}\right|\).
Solution:
Given, \(\frac{\mathbf{z}_2}{\mathbf{z}_1}\), z₁ is an imaginary numbers.
⇒ \(\frac{\mathbf{z}_2}{\mathbf{z}_1}\) = ki (say)

Question 33.
If z = x + iy and if the point P in the Argand plane represents z, then describe geometrically the locus of P satisfying the equations
(i) |2z – 3| = 7
(ii) |z|² = 4Re(z + 2)
(iii) |z + i|² – |z – i|² = 2
(iv) |z + 4i| + |z – 4i| = 10
Solution:
(i) Given,
z = x + iy
⇒ P = (x, y)
|2z – 3| = 7
|2(x + iy) – 3| = 7
|2x + 2iy – 3| = 7
|(2x – 3) + i2y| = 7
\(\sqrt{(2 x-3)^2+(2 y)^2}\) = 7
Squaring on both sides,
(2x – 3)² + (2y)² = 49
4x² + 9 – 12x + 4y² – 49 = 0
4x² + 4y² – 12x – 40 = 0
x² + y² – 3x – 10 = 0
∴ Locus of P is x² + y² – 3x – 10 = 0
The locus represents a circle with centre at (\(\frac{3}{2}\), o) and radius \(\frac{7}{2}\) units.

(ii) Given, z = x + iy
⇒ P = (x, y)
|z|² = 4 Re(z + 2)
|x + iy|² = 4 Re(x + iy + 2)
\(\left(\sqrt{x^2+y^2}\right)^2\) = 4 Re(x + 2 + iy)
x² + y² = 4 (x + 2)
x² + y² = 4x + 8
x² + y² – 4x – 8 = 0
Locus of P is x² + y² – 4x – 8 = 0
The locus represents a circle with centre at (2, 0) and radius 2√3 units.

(iii) Given, z = x + iy
⇒ P = (x, y)
|z + i|² – |z – i|² = 2
|x + iy + i|² – |x + iy – i|² = 2
|x + i(y + 1)|² – |x + i(y – 1)²| = 2
\(\left(\sqrt{(x)^2+(y+1)^2}\right)^2-\left(\sqrt{x^2+(y-1)^2}\right)^2\) = 2
x² + (y + 1)² – (x² + (y – 1)²) = 2
x² + (y + 1)² – x² – (y – 1)² = 2
y² + 2y + 1 – y² + 2y – 1 – 2 = 0
4y – 2 = 0
2y – 1 = 0
∴ Locus of P is 2y – 1 = 0
The locus represents a straight line parallel to X – axis.

(iv) Given, z = x + iy
⇒ P = (x, y)
|z + 4i| + |z – 4i| = 10
|x + iy + 4i| + |x + iy – 4i| = 10
|x + i(y + 4)| + |x + i(y – 4)| = 10
\(\sqrt{x^2+(y+4)^2}+\sqrt{x^2+(y-4)^2}\) = 10
\(\sqrt{x^2+(y+4)^2}\) = 10 – \(\sqrt{x^2+(y-4)^2}\)
Squaring on both sides,
x² + (y + 4)² = 100 + (x² + (y – 4)²) – 20 \(\sqrt{x^2+(y-4)^2}\)
x² + y² + 16 + 8y = 100 + x² + y² + 16 – 8y – 20 \(\sqrt{x^2+y^2+16-8 y}\)
8y + 8y – 100 = – 20 \(\sqrt{x^2+y^2+16-8 y}\)
16y – 100 = – 20 \(\sqrt{x^2+y^2+16-8 y}\)
4y – 25 = – 5 \(\sqrt{x^2+y^2+16-8 y}\)
Again squaring on both sides
16y² + 625 – 200y = 25(x² + y² + 16 – 8y)
16y² + 625 – 200y = 25x² + 25y² 400 – 200y
25x² + 25y² + 400 – 16y – 625 = 0
25x² + 9y² – 225 = 0
25x² + 9y² = 225
\(\frac{x^2}{9}+\frac{y^2}{25}\)
∴ Locus of P is \(\frac{x^2}{9}+\frac{y^2}{25}\)= 1.

The locus represents an ellipse with centre (0, 0) with eccentricity \(\frac{4}{5}\) and major axis is parallel to Y – axis.

Question 34.
If z₁, z₂ are two non-zero complex numbers satisfying |z₁ + z₂| = |z₁ + z₂| then show that Arg z₁ – Arg z₂ = 0.
Solution:
Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ then
|z₁ + z₂| = |x₁ + iy₁ + x₂ + iy₂|
= |(x₁ + x₂) + i(y₁ + y₂)|
= \(\sqrt{\left(\mathrm{x}_1+\mathrm{x}_2\right)^2+\left(\mathrm{y}_1+\mathrm{y}_2\right)^2}\)
and |z₁| = |x₁ + iy₁|
= \(\sqrt{x_1^2+y_1^2}\)
|z₂| = |x₂ + iy₂|
= \(\sqrt{\mathrm{x}_2^2+\mathrm{y}_2^2}\)

Given that,
|z₁ + z₂| = |z₁| + |z₂|
\(\sqrt{\left(x_i+x_2\right)^2+\left(y_1+y_2\right)^2}\) = \(\sqrt{x_1^2+y_1^2}+\sqrt{x_2^2+y_2^2}\)

Squaring on both sides,
(x₁ + x₂)² + (y₁ + y₂)² = x₁² + y₁² + x₂² + y₂² + 2 \(\sqrt{\left(x_1^2+y_1^2\right)} \sqrt{x_2^2+y_2^2}\)

x₁² + x₂² + 2x₁x₂ + y₁² + y₂² + 2y₁y₂ = x₁² + y₁² + x₂² + y₂² + 2 \(\sqrt{x_1^2+y_1^2} \sqrt{x_2^2+y_2^2}\)

2x₁x₂ + 2y₁y₂ = 2 \(\sqrt{x_1^2+y_1^2} \sqrt{x_2^2+y_2^2}\)
x₁x₂ + y₁y₂ = \(\sqrt{x_1^2+y_1^2} \sqrt{x_2^2+y_2^2}\)
Again squaring on both sides,
(x₁x₂ + y₁y₂)² = (x₁² + y₁²) (x₂² + y₂²)
x₁²x₂² + y₁²y₂² + 2x₁x₂y₁y₂ = x₁²x₂² + x₁²y₂² + x₂² y₂² + y₁² y₂²
x₁² y₂² + x₂² y₁² – 2 x₁ x₂y₁ y₂ = 0
(x₁y₂ – x₂ y₁)² = 0
x₁y₂ – x₂ y₁ = 0
x₁y₂ = x₂ y₁
\(\frac{\mathrm{y}_2}{\mathrm{x}_2}=\frac{\mathrm{y}_1}{\mathrm{x}_1}\)
\(\frac{\mathrm{y}_1}{\mathrm{x}_1}=\frac{\mathrm{y}_2}{\mathrm{x}_2}\)
\(\tan ^{-1}\left(\frac{\mathrm{y}_1}{\mathrm{x}_1}\right)=\tan ^{-1}\left(\frac{\mathrm{y}_2}{\mathrm{x}_2}\right)\)
Arg z₁ = Arg z₂
Arg z – Arg z₂ = 0.

Question 35.
Describe geometrically the subsets of ‘C’ suchthat {z ∈ C/|z – 1 + i|= i}
Solution:
Let z = x + iy
⇒ P = (x, y)
Let,
C = {z ∈ C/|x + iy – 1 + i| = 1}
= {(x, y) ∈ R²/|x + iy – 1 +i| = i}
= {(x, y) ∈ R²/|(x – 1) + i(y + 1)i = i}
={(x, y)∈ R²/(x – 1)² + (y + 1)² = i}
Hence C is a circle with centre (1, – 1) and radius 1 unit.

Question 36.
If z = x + iy and if the point P in the Argand plane represents z, then describe geometrically the locus of z satisfying the equations
(i) 2|z – 2| = |z – 1|
(ii) Im z² = 4
(iii) Arg \(\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
Solution:
(i) Given, z = x + iy
2|z – 2| = |z – 1|
2|x + iy – 2| = |x + iy – 1|
2|(x – 2) + iy| = |(x – 1) + iy|
2\(\sqrt{(x-2)^2+y^2}=\sqrt{(x-1)^2+y^2}\)
Squaring on both sides,
4(x – 2)² + 4y² = (x – 1)² + y²
4(x² – 4x + 4) + 4y² = (x² – 2x + 1) + y²
4x² – 16x + 16 + 4y² – x² + 2x – 1 – y² = 0
3x² + 3y² – 14x + 15 = 0
∴ Locus of P is 3x² + 3y² – 14x + 15 = 0.
Locus represents a circle with centre (\(\frac{7}{3}\) , 0) and radius \(\frac{2}{3}\) units.

(ii) Given, z = x + iy
⇒ P = (x, y)
Given, Imz² = 4
Im (x + iy)² = 4
Im (x² – y² + 2ixy) = 4
2xy = 4
xy = 2
∴ The locus of P is xy = 2
The locus represents a rectangular hyperbola.

(iii) Given, z = x + iy P = (x, y)
Now, \(\frac{z-1}{z+1}=\frac{x+i y-1}{x+i y+1}=\frac{(x-1)+i y}{(x+1)+i y}\)

2y = x² + y² – 1
x² + y² – 2y – 1 = 0
∴ Locus of P is x² + y² – 2y – 1 = 0
∴ The locus represents a circle with centre (0, 1) and radius √2 units.

Question 37.
If \(\frac{\mathbf{z}_3-\mathbf{z}_1}{\mathbf{z}_2-\mathbf{z}_1}\) is a real number, show that the points represented by the complex numbers z₁, z₂, z₃ are collinear.
Solution:
Given that,
\(\frac{\mathbf{z}_3-\mathbf{z}_1}{\mathbf{z}_2-\mathbf{z}_1}\) is a real number.
⇒ \(\frac{\mathbf{z}_3-\mathbf{z}_1}{\mathbf{z}_2-\mathbf{z}_1}\) = k (say)
z₃ – z₁ = k (z₂ – z₁)
z₃ – z₁ = kz₂ – kz₁
z₃ – kz₂ = z₁ – kz₁
z₃ – kz₂ = z₁ (1 – k)
z₁ = \(\frac{\mathrm{z}_3-\mathrm{kz}_2}{1-\mathrm{k}}\)

z₁ represents a point on the Line joining, the points represented by z₂, z₃ in the ratio 1 : k externally.
∴ z₁, z₂, z₃ are collinear.

Question 38.
Show that the four points in the Argand plane represented by the complex numbers 2 + i, 4 + 3i, 2 + 5i, 3i are vertices of a square.
Solution:

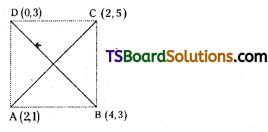
Let, the given points are A (2, 1), B (4, 3), C(2, 5), D(0, 3)
AB = \(\sqrt{(2-4)^2+(1-3)^2}\)
= \(\sqrt{(-2)^2+(-2)^2}=\sqrt{4+4}=\sqrt{8}\)

BC = \(\sqrt{(4-2)^2+(3-5)^2}\)
= \(\sqrt{(2)^2+(-2)^2}=\sqrt{4+4}=\sqrt{8}\)

CD = \(\sqrt{(2-0)^2+(5-3)^2}\)
= \(\sqrt{(2)^2+(2)^2}=\sqrt{4+4}=\sqrt{8}\)

DA = \(\sqrt{(2-0)^2+(1-3)^2}\)
= \(\sqrt{(2)^2+(-2)^2}=\sqrt{4+4}=\sqrt{8}\)

AC = \(\sqrt{(2-2)^2+(1-5)^2}\)
= \(\sqrt{0+(-4)^2}=\sqrt{0+16}=4\)

BD = \(\sqrt{(4-0)^2+(3-3)^2}\)
= \(\sqrt{(4)^2+0}=\sqrt{16}=4\)

∴ AB = BC = CD = DA and AC = BD.
∴ The given points form a square.

Question 39.
Show that the points in the Argand diagram represented by the complex numbers z₁, z₂, z₃are colilnear if and only if there exist three real numbers p, q, r not all zero, satisfying pz₁ + qz₂ + rz₃ = 0 and p + q + r = 0.
Solution:

z₁, z₂, z₃ are collinear then z₃ lies on the line joining z₁ and z₂.
⇒ z₃ = \(\frac{\mathrm{mz}_2+\mathrm{nz}_1}{\mathrm{~m}+\mathrm{n}}\)
⇒ z₃ (m + n) = mz₂ + nz₁
⇒ nz₁ + mz₂ – (m + n) z₃ = 0
which is of the form pz₁ + qz₂ + rz₃ = 0
where
p = n, q = m, r = – m – n
Now, p + q + r = n + m – m – n = 0
∴ p + q + r = 0.

Question 40.
Represent the complex number 2 + 3i in Argand plane. [TS – Mar.2015]
Solution:
In Argand plane the complex number 2 + 3i is represented as the point (2, 3).