TS Inter 1st Year Maths 1A Product of Vectors Important Questions Long Answer Type

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Product of Vectors Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Product of Vectors Important Questions Long Answer Type

Question 1.
By the vector method, prove that altitudes of a triangle are concurrent.
Answer:
Let A, B, C be the vertices of a triangle.
Let \(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OC}}\) = c̅
Let the altitudes through A, B meet at H and \(\overline{\mathrm{OH}}\) = r̅ (say)

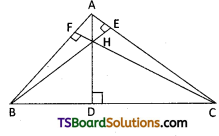
Now \(\overline{\mathrm{AH}} \perp \overline{\mathrm{BC}} \Rightarrow \overline{\mathrm{AH}} \cdot \overline{\mathrm{BC}}=0 \Rightarrow(\overline{\mathrm{OH}}-\overline{\mathrm{OA}}) \cdot(\overline{\mathrm{OC}}-\overline{\mathrm{OB}})\) = 0
⇒ (r̅ – a̅). (c̅ – b̅) = 0
⇒ r̅ . (c̅ – b̅) – a̅. (c̅ – b̅) = 0 ……………(1)

Also \(\overline{\mathrm{BH}} \perp \overline{\mathrm{AC}} \Rightarrow \overline{\mathrm{BH}} \cdot \overline{\mathrm{AC}}=0 \Rightarrow(\overline{\mathrm{OH}}-\overline{\mathrm{OB}}) \cdot(\overline{\mathrm{OC}}-\overline{\mathrm{OA}})\) = 0
⇒ (r̅ – b̅). (c̅ – a̅) = 0
⇒ r̅ .(c – a̅) – b̅.(c̅ – a̅) = 0 ………….(2)

(1) – (2) ⇒ r̅ . (c̅ – b̅) – a̅. (c̅ – b̅) – r . (c̅ – a̅) + b̅. (c̅ – a̅) = 0

⇒ r̅ . (a̅ – b̅) – c̅ (a̅ – b̅) = 0
⇒ (r̅ – c̅) . (a̅ – b̅) = 0
⇒ \((\overline{\mathrm{OH}}-\overline{\mathrm{OC}}) \cdot(\overline{\mathrm{OA}}-\overline{\mathrm{OB}})\) = 0
⇒ \((\overline{\mathrm{OH}}-\overline{\mathrm{OC}}) \cdot(\overline{\mathrm{OA}}-\overline{\mathrm{OB}})=0 \Rightarrow \overline{\mathrm{CH}} \cdot \overline{\mathrm{BA}}=0 \Rightarrow \overline{\mathrm{CH}} \perp \overline{\mathrm{BA}}\)
∴ The altitude through C also passes through H.
∴ The altitudes of a Ale are concurrent.

Question 2.
By vector method, prove that the perpendicular bisectors of the sides of a triangle are concurrent. [Mar. ’92]
Answer:
Let A, B, C be the vertices of a triangle. Let \(\overline{\mathrm{OA}}\) = a, \(\overline{\mathrm{OB}}\) = b, \(\overline{\mathrm{OC}}\) = c

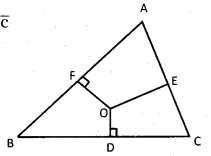
Let D, E, F are the midpoints of BC, CA, AB respectively

∴ The bisector of AB passes through ‘O’.
∴ The perpendicular bisectors of a triangle are concurrent.

Question 3.
If a̅, b̅, c̅ be three vectors. Then show that (a̅ × b̅) × c̅ = (a̅. c̅) b̅ – (b̅ . c̅) a̅.
Answer:
Let a̅ = a₁ i̅ + a₂ j̅ + a₃k̅, b̅ = b₁ i̅ + b₂ j̅ + b₃k̅ and c̅ = c₁ i̅ + c₂ j̅ + c₃k̅
= i̅ (a₂b₃ – a₃b₂) – j̅ (a₁b₃ – a₁b₃) + k̅ (a₁b₂ – a₂b₁)

(a̅ × b̅) × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
a_2 b_3-a_3 b_2 & a_3 b_1-a_1 b_3 & a_1 b_2-a_2 b_1 \\
c_1 & c_2 & c_3
\end{array}\right|\)
= i̅(a₃b₁c₃ – a₁b₃c₃ – a₁b₂c₂ + a₂b₁c₂) – j̅(a₂b₃c₃ – a₃b₂c₃ – a₁b₂c₁ + a₂b₁c₁) + k̅ (a₂b₃c₂ – a₃b₂c₂ – a₃b₁c₁ + a₁b₃c₁)
c̅.a̅ = (c₁i̅ + c₂j̅ + c₃k̅). (a₁i̅ + a₂j̅ + a₃k̅) = c₁a₁ + c₂a₂ + c₃a₃
c̅.b̅ = (c₁i̅ + c₂j̅ + c₃k̅). (b₁̅ + b₂j̅ + b₃k̅) = c₁b₁ + c₂b₂ + c₃b₃

Now (c̅.a̅)b̅ – (c̅.b̅)a̅ = (c₁a₁ + c₂a₂ + c₃a₃) (b₁ i + b₂ j + b₃k) – (c₁b₁ + c₂b₂ + c₂b₃) (a₁ i̅ + a₂j̅ + a₃k̅)
= a₁b₁c₁ i̅ + a₁b₂c₁ j̅ + a₁b₃c₁ k̅ + a₂b₁c₂ i̅ + a₂b₂c₂j̅ + a₂b₃c₂ k̅ + a₃b₁c₃ i̅ + a₃b₂c₃ i̅ + a₃b₂c₃ j̅ + a₃b₃c₃ k̅ – a₁b₁c₁i̅ – a₂b₁c₁j̅ – a₃b₂₁c₁ k̅ – a₁b₂c₂ i̅ – a₁b₂c₂ j̅ – a₃b₂c₂k̅ – a₁b₃c₃i̅ – a₂b₃c₃j̅ – a₃b₃c₃k̅
= i̅(a₂b₁c₂ + a₃b₁c₃ – a₁b₂c₂ – a₁b₃c₃) – j̅(-a₁b₂c₁ – a₃b₂c₃ + a₂b₁c₁ + a2₂b₃c₃) + k̅(a₁b₃c₁ + a₂b₃c₂ – a₃b₁c₁ – a₃b₂c₂)
∴ (a̅ × b̅) × c̅ = (a̅. c̅) b̅ – (b̅ . c̅) a̅

Question 4.
Find the equation of the plane passing through the points A = (2, 3, -1), B = (4, 5, 2) and C = (3, 6, 5).
Answer:
Let the position vectors of the points A, B and C with respect to the origin ‘O’ are
\(\overline{\mathrm{OA}}\) = 2 i̅ + 3 j̅ – k̅; \(\overline{\mathrm{OB}}\) = 4 i̅ + 5 j̅ + 2k̅; \(\overline{\mathrm{OC}}\) = 3 i̅ + 6 j̅ + 5k̅
Let r̅ = OP = x i̅ + y j̅ + zk̅ be the position vector of any point P in the plane of ΔABC.
AP = OP-OA = xi̅ + yj̅ + zk̅ – 2i̅ – 3j̅ + k̅ = (x – 2)i̅ + (y – 3)j̅ +(z + 1)k̅
AB = OB – OA = 4i̅ + 5j̅ + 2k̅ – 2i̅ – 3j̅ + k̅ = 2i̅ + 2j̅ + 3k̅
AC = OC -OA = 3i̅ + 6j̅ + 5k̅ – 2i̅ – 3j̅ + k̅ = i̅ + 3j̅ + 6k̅
The equation of the plane passing through the points A, B and C is \([\overline{\mathrm{AP}} \overline{\mathrm{AB}} \overline{\mathrm{AC}}]\) = 0
⇒ \(\left|\begin{array}{ccc}
x-2 & y-3 & z+1 \\
2 & 2 & 3 \\
1 & 3 & 6
\end{array}\right|\) = 0
⇒ (x – 2) [12 – 9] – (y – 3) [12 – 3] + (z + 1) [6 – 2] = 0
⇒ (x – 2) (3) – (y – 3) (9) + (z + 1) (4) = 0
⇒ 3x – 6 – 9y + 27 + 4z + 4 = 0
⇒ 3x – 9y + 4z + 25 = 0.

Question 5.
Find the equation of the plane passing through the point A = (3, -2, -1) and parallel to the vectors b̅ = i̅ – 2j̅ + 4k̅ and c̅ = 3i̅ + 2j̅ – 5k̅. [May ’01]
Answer:
The position vector of the point with respect to origin O’ is OA = 3 i̅ – 2 j̅ – k̅
Given b = i̅ – 2j̅ + 4k̅, c = 3i̅ + 2j̅ – 5k̅
Let r̅ = \(\overline{\mathrm{OP}}\) = xi̅ + yj̅ + zk̅ be the position vectqr of any point P in the plane of AABC.
\(\overline{\mathrm{AP}}=\overline{\mathrm{OP}}-\overline{\mathrm{OA}}\) = xi̅ +yj̅ + zk̅ – 3i̅ +2j̅ + k̅ = (x – 3)i̅ +(y + 2)j̅ +(z + 1)k̅

The equation of the plane passing through the point A parallel to the vectors b̅ & c̅ is [\(\overline{\mathrm{AP}} b̅ c̅ ] = 0
⇒ \left|\begin{array}{ccc}
x-3 & y+2 & z+1 \\
1 & -2 & 4 \\
3 & 2 & -5
\end{array}\right|\) = 0
⇒ (x – 3)[10 – 8] – (y + 2)[-5 – 12] + (z + 1)[2 + 6] = 0
⇒ (x + 3)(2) – (y + 2)(-17) + (z + 1)(8) = 0
⇒ 2x – 6 + 17y + 34 + 8z + 8 = 0
⇒ 2x + 17y + 8z + 36 = 0.

Question 6.
Find the shortest distance between the skew lines r̅ = (6i̅ + 2j̅ + 2k̅) + t (i̅ – 2j̅ + 2k̅) and r̅ = (-4i̅ – k̅) + s (3i̅ – 2j̅ – 2k̅).
Answer:
Given equations of the straight lines are r̅ = (6 i̅ + 2j̅ +2k̅) + t(i̅ – 2j̅ + 2k̅)

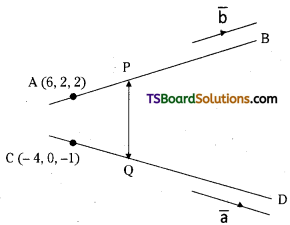
Comparing this equation with r̅ = a̅ + tb̅
a̅ = 6 i̅ + 2 j̅ + 2k̅, b̅ = i̅ – 2j̅ + 2k̅
r̅ = (- 4 i̅ – k̅) + s (3 i̅ – 2 j̅ – 2k̅)

Comparing this equation with r̅ = c̅ + sd̅
c̅ = -4i̅ – k̅, d̅ = 3i̅ – 2j̅ – 2k̅
a̅ – c̅ = 6i̅ + 2j̅ + 2k̅ + 4i̅ + k ̅= 10i̅ + 2j̅ + 3k̅
[a̅ – c̅ b̅d̅] = \(\left|\begin{array}{ccc}
10 & 2 & 3 \\
1 & -2 & 2 \\
3 & -2 & -2
\end{array}\right|\) = 10(4 + 4) – 2(-2-6) + 3(-2 + 6)
= 10(8) – 2(-8) + 3(4) = 80 + 16 + 12 = 108

b̅ × d̅ =
= i̅(4 + 4) – j̅(-2-6) + k̅(-2+6) = 8i̅ + 8j̅ + 4k̅

|b̅ × d̅| = \(\sqrt{8^2+8^2+4^2}\)
= \(\sqrt{64+64+16}=\sqrt{144}\)
= 12

The shortest distance between the two skew lines is
PQ = \(\frac{\mid\left[\begin{array}{ll}
\overline{\mathrm{a}}-\overline{\mathrm{c}} & \overline{\mathrm{b}} \overline{\mathrm{d}}]
\end{array} \mid\right.}{|\overline{\mathrm{b}} \times \overline{\mathrm{d}}|}=\frac{|108|}{12}=\frac{108}{12}\) = 9

Question 7.
If A = (1, – 2, – 1), B = (4,0, – 3), C = (1, 2, – 1) and D = (2, – 4, – 5), find the distance between \(\overline{\mathrm{A B}}\) and \(\overline{\mathrm{C D}}\).
Answer:
Given points are A = (1, – 2, – 1), B = (4, 0, – 3), C = (1, 2, – 1), D = (2, -4,-5)

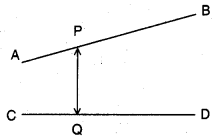
The vector equation of the straight line passing through the points A and B is
r = (1 – t)a̅ + tb̅, t ∈ R = (1 – t) (i̅ – 2j̅ – k̅) + t(4 i̅ – 3k̅) = i̅ – 2j̅ – k̅ – ti̅ + 2t j̅ + tk̅ + 4ti̅ – 3tk̅
= (i̅ – 2j̅ – k̅) + 3ti̅ +2tj̅ – 2tk̅
r = (i̅ – 2j̅ – k̅) + t(3i̅ + 2j̅ – 2k̅)

Comparing this equation with r̅ = a̅ + tb̅
We get a̅ = i̅ – 2 j̅ – k̅, b̅ = 3 i̅ + 2 j̅ – 2k̅

The vector equation of a straight line passing through the points C and D is
r̅ = (1 – s) c̅ + sd̅, s ∈ R = (1 – s) (i̅ + 2j̅ – k̅) + s(2i̅ – 4j̅ – 5k̅)
= i̅ + 2j̅ – k̅ – si̅ — 2s j̅ + sk̅ + 2si̅ – 4s j̅ – 5sk̅
= i̅ + 2j̅ – k̅ + si̅ – 6sj̅ – 4sk̅
r = (i̅ – 2 j̅ – k̅) + s(i̅ – 6j̅ – 4k̅)

Comparing this equation with r = c̅ + sd̅, we get c̅ = i̅ + 2j̅ – k̅, d̅ = i̅ – 6j̅ – 4k̅
a̅ – c̅ = i̅ – 2j̅ – k̅ – i̅ – 2j̅ + k̅ = – 4j̅
[a̅ – c̅ b̅d̅] = \(\left|\begin{array}{rrr}
0 & -4 & 0 \\
3 & 2 & -2 \\
1 & -6 & -4
\end{array}\right|\)
= 0(-8 – 12) + 4(-12 + 2) + 0(-18 – 2) = 0 + 4(-10) + 0 = -40

b̅ × d̅ = \(\left|\begin{array}{ccc}
\overline{\mathbf{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 2 & -2 \\
1 & -6 & -4
\end{array}\right|\)
= i̅(-8 – 12) – j̅(-12 + 2) + k̅(-18 – 2) = 20i̅ + 10j̅ – 20k̅

b̅ × d̅ = \(\sqrt{(-20)^2+(10)^2+(-20)^2}\)
= \(\sqrt{400+100+400}=\sqrt{900}\)
= 30

The shortest distance between the two skew lines is PQ = \(\frac{\left|\left[\begin{array}{ll}
\bar{a}-\bar{c} & \bar{b} \bar{d}
\end{array}\right]\right|}{|\bar{b} \times \bar{d}|}=\frac{|-40|}{30}=\frac{4}{3}\)

Question 8.
If a̅ = i̅ – 2j̅ + k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + 2j̅ – k̅ find a̅ × (b̅ × c̅) and |(a̅ × b̅) × c̅|.
Answer:
Given vectors are a̅ = i̅ – 2j̅ + k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + 2j̅ – k̅

Question 9.
If a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅ and c̅ = i̅ + 3j̅ – 2k̅, verify that a̅ × (b̅ × c̅) = (a̅ × b̅) × c̅. [Mar ’11, ’98; Mar. ’08, ’04; B.P]
Answer:
Given vectors a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅

Question 10.
If a̅ = 2i̅ + j̅ – 3k̅, b̅ = i̅ – 2j̅ + k̅, c̅ = – i̅ + j̅ – 4k̅ and d̅ = i̅ + j̅ + k̅, then compute |(a̅ × b̅) × (c̅ × d̅)|. [Mar. ’15(TS); Mar. ’03]
Answer:
Given vectors are a̅ = 2i̅ + j̅ – 3k̅, b̅ = i̅ – 2j̅ + k̅, c̅ = – i̅ + j̅ – 4k̅, d̅ = i̅ + j̅ + k̅

Question 11.
If a̅ = i̅ – 2j̅ + 3k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + j̅ + 2k̅, then find |(a̅ × b̅) × c̅| and |a̅ × (b̅ × c̅)|. [Mar. ’18(TS); Mar ’13]
Answer:
Given vectors are a̅ = i̅ – 2j̅ + 3k̅, b̅ = 2i̅ + j̅ + k̅, c̅ = i̅ + j̅ + 2k̅
Now (a̅ × b̅) × c̅ = (a̅. c̅)b̅ – (b̅. c̅) a̅
= [(i̅ – 2j̅ + 3k̅). (i̅ + j̅ + 2k̅)] b̅ – [(2i̅ + j̅ + k̅). (i̅ + j̅ + 2k̅)]a̅
= (1 – 2 + 6)b̅ – (2 + 1 + 2)a̅ = 5b̅ – 5a̅
= 5 [2i̅ + j̅ + k̅ – i̅ + 2j̅ – 3k̅] = 5 [i̅ + 3j̅ – 2k̅]
|(a̅ × b̅) × c̅| = 57l + 9 + 4 = 57l4

a̅ × (b̅ × c̅) = (a̅. c̅)b̅ – (a̅. b̅) c̅
= [(i̅ – 2j̅ + 3k̅). (i̅ + j̅ + 2k̅)] b̅ – [(i̅ – 2j̅ + 3k̅). (2i̅ + j̅ + k̅)]c̅
= (1 – 2 + 6) b̅ – (2 – 2 + 3) c̅ = 5b̅ – 3c̅
= 5 (2 i̅ + j̅ + k̅) — 3(i̅ + j̅ + 2k̅) = 7 i̅ + 2 j̅ – k̅
Hence |a̅ × (b̅ × c̅) | = |7i̅ + 2j̅ – k̅|
= \(\sqrt{49+4+1}=\sqrt{54}\) = 3√6

Question 12.
Let a̅ = 2i + j – 2k, b̅ = i + j. If c isavec- tor such that a̅.c̅ = |c̅|,|c̅-a̅| = 2√2 and the angle between a̅ × b̅ and c is 30°, then find the value of |(a̅ × b̅) × c̅|. [May ’15(TS)]
Answer:
Given that a̅ = 2i̅ + j̅ – 2k̅, b̅ = i̅ + j̅
⇒ |a̅| = \(\sqrt{4+1+4}\) = √9 =3, |b̅| = \(\sqrt{1+1}\) = √2
also, a̅ . c̅ = |c̅| and |c̅ – a̅| = 2√2
⇒ (c̅ – a̅)² = 8 ⇒ |c̅|² + |a̅|² – 2c̅.a̅ = 8
⇒ |c| + 9 – 2|c̅| = 8 ⇒ |c̅| — 2|c̅| + 1 = 0
⇒ (|c̅| – 1) = 0 ⇒ |c̅| = 1

Now a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 1 & -2 \\
1 & 1 & 0
\end{array}\right|\)
= i̅(0 + 2) – j̅(0 + 2) + k̅ (2 – 1) = 2i̅ – 2j̅ + k̅
|a̅ × b̅| = ^/4 + 4 + l =3
|(a̅ × b̅) × c̅| = |a̅ × b̅| |c̅| sin (a̅ × b̅, c̅)
= |a̅ × b̅| |c̅| sin 30° = 3.1.\(\frac{1}{2}=\frac{3}{2}\)

Some More Maths 1A Product of Vectors Important Questions

Question 1.
If a̅ = 6i̅ + 2j̅ + 3k̅ and b̅ = 2i̅ – 9j̅ + 6k̅ then find a̅. b̅ and the angle between a̅ and b̅.
Answer:
Given a̅ = 6i̅ + 2j̅ + 3k̅ and b̅ = 2i̅ – 9j̅ + 6k̅
Now a̅.b̅ = (6i̅ + 2j̅ + 3k̅).(2i̅ – 9j̅ + 6k̅) = 12 – 18 + 8 = 12

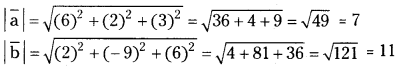
Let ‘θ’ be the angle between a̅ & b̅ then cos θ = \(\frac{\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}}{|\overline{\mathrm{a}}||\overline{\mathrm{b}}|}=\frac{12}{7.11}=\frac{12}{77}\)
∴ θ = cos^-1\(\left(\frac{12}{77}\right)\)

Question 2.
For what values of λ, the vectors i̅ – λj̅ + 2k̅ and 8i̅ + 6 j̅ – k̅ are at right angles ?
Answer:
Let a̅ = i̅ – λj̅ + 2k̅ and b̅ = 8i̅ + 6j̅ – k̅
Since a,b form a right angle i.e., the vectors a and b are perpendicular then a̅ b̅ =0
(i̅ – λj̅ + 2k̅). (8i̅ + 6j̅ – k̅) = 0
⇒ 8 – 6λ – 2 = 0
⇒ 6 – 6λ = 0
⇒ 6λ = 6
⇒ λ = 1.

Question 3.
If the vectors λi̅ – 3j̅ + 5k̅ and 2λi̅ – A,j̅ – k̅ are perpendicular to each other then find X.
Answer:
Let a̅ = λi̅ – 3j̅ + 5k̅ and b̅ = 2λi̅ – λj̅ – k̅
Since the vector a̅ = λi̅ – 3j̅ + 5k̅ and b̅ = 2λi̅ – λj̅ – k̅
(λi̅ – 3j̅ + 5k̅). (2λ.i̅ – λ j̅ -k̅) = 0
2λ² + 3λ – 5 = 0
2λ² + 5λ – 2λ – 5 = 0

λ(2λ + 5) – 1(2λ + 5) = 0
(2λ + 5) (λ – 1) = 0
2λ + 5 = 0, λ – 1 = 0
λ = \(\frac{-5}{2}\), λ = 1
∴ λ = \(\frac{-5}{2}\) (or) 1.

Question 4.
If a̅ = i̅ – j̅ – k̅ and b̅ = 2i̅ – 3j̅ + k̅, then find the projection vector of b on a and its magnitude.
Answer:
Given vectors are a̅ = i̅ – j̅ – k̅ and b̅ = 2 i̅ – 3 j̅ + k̅
The projection vector of b̅ on a̅

Question 5.
Find the area of the parallelogram for which the vectors a̅ = 2i̅ – 3j̅ and b̅ =3i̅ – k̅ are adjacent sides.
Answer:
Given vectors are = 2j̅ – 3j̅ and b̅ = 3i̅ – k̅
The area of the parallelogram for which the vectors and 6 are adjacent sides
= a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & -3 & 0 \\
3 & 0 & -1
\end{array}\right|\)
= i̅(3 – o) – j̅(-2 – o) + k̅(0 + 9) = 3i̅ + 2j̅ + 9k̅
∴ Area of the parallelogram = |a̅ × b̅| = \(\sqrt{(3)^2+(2)^2+(9)^2}=\sqrt{9+4+81}=\sqrt{94}\) sq.units.

Question 6.
If a̅ = 2i̅ – 3j̅ + 5k̅, b̅ = -i̅ + 4j̅ + 2k̅ then find a̅ × b̅ and unit vector perpendicular to both a̅ and b̅.
Answer:
Given a̅ = 2i̅ – 3j̅ + 5k̅, b̅ = -i̅ + 4j̅ + 2k̅
a̅ × b̅ =
= i̅(-6 – 20) – j̅(4 + 5) + k(8 – 3) = 26i̅ – 9j̅ + 5k̅
|a̅ × b̅| = \(\sqrt{(-26)^2+(-9)^2+(5)^2}=\sqrt{676+81+25}\)
= \(\sqrt{782}\)
∴ The unit vector perpendicular to both a̅ & b̅ is = \(\frac{(\overline{\mathrm{a}} \times \overline{\mathrm{b}})}{|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}=\pm \frac{(-26 \overline{\mathrm{i}}-9 \overline{\mathrm{j}}+5 \overline{\mathrm{k}})}{\sqrt{782}}\)

Question 7.
Find unit vector perpendicular to both i̅ + j̅ + k̅ and 2i̅ + j̅ + 3k̅.
Answer:
Let a̅ = i̅ + j̅ + k̅, b̅ = 2i̅ + j̅ + 3k̅
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
2 & 1 & 3
\end{array}\right|\)
= i̅(3 – 1) – j̅(3 – 2) + k̅(1 – 2)
= 2i̅ – j̅ – k̅
|a̅ × b̅| = \(\sqrt{(2)^2+(-1)^2+(-1)^2}=\sqrt{4+1+1}\) = √6
∴ The unit vector perpendicular to both a̅ & b̅ is = \(\pm \frac{(\overline{\mathrm{a}} \times \overline{\mathrm{b}})}{|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}=\pm \frac{(2 \overline{\mathrm{i}}-\overline{\mathrm{j}}-\overline{\mathrm{k}})}{\sqrt{6}}\)

Question 8.
If θ is the angle between the vector i̅ + j̅ and j̅ + k̅, then find sin θ.
Answer:
Let a̅ = i̅ + j̅ , b̅ = j̅ + k̅
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 0 \\
0 & 1 & 1
\end{array}\right|\)
= i̅(1 – 0) – j̅(1 – 0) + k̅(1 – 0) = i̅ – j̅ + k̅

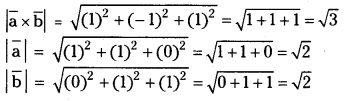
If ‘θ’ is the angle between the vector a̅ & b̅ then sin θ = \(\frac{(\overline{\mathrm{a}} \times \overline{\mathrm{b}})}{|\overline{\mathrm{a}}| \overline{\mathrm{b}} \mid}=\frac{\sqrt{3}}{\sqrt{2} \cdot \sqrt{2}}=\frac{\sqrt{3}}{2}\)

Question 9.
If a̅ = (1, – 1, -6), b̅ = (1, -3, 4) and c̅ = (2, -5, 3), then compute a̅.(b̅ × c̅).
Answer:
Given a̅ = (1, – 1, -6), b̅ = (1, -3, 4), c̅ = (2, -5, 3)
Now a̅.(b̅ × c̅) = [a̅ b̅ c̅]= 1 —3 4
= 1(-9 + 20) + 1(3 – 8) – 6(-5 + 6)
= 11 – 5 – 6 = 0

Question 10.
Find the volume of the parallelopiped whose coterminus edges are represented by the vectors 2i̅ – 3j̅ + k̅, i̅ -j̅ + 2k̅ and 2i̅ + j̅ – k̅ .
Answer:
Let a̅ = 2i̅ – 3j̅ + k̅, b̅ = i̅ -j̅ + 2k̅, c̅ = 2i̅ + j̅ – k̅
Volume of the parallelopiped
V = |[a̅ b̅ c̅]|
[a̅ b̅ c̅] = \(\left|\begin{array}{rrr}
2 & -3 & 1 \\
1 & -1 & 2 \\
2 & 1 & -1
\end{array}\right|\) = 2(1 – 2) + 3(-1-4) + 1(1 + 2)
= -2 – 15 + 3 = -14

∴ |[a̅ b̅ c̅]| = 14 cubic units

Question 11.
Find ‘t’ for which the vectors 2i̅ – 3j̅ + k̅, i̅ + 2j̅ – 3k̅ and j̅ – tk̅ are coplanar.
Answer:
Let a̅ = 2i̅ – 3j̅ + k̅, b̅ = i̅ + 2j̅ – 3k̅, c̅ = j̅ – tk̅
Since the vectors are coplanar then [a̅ b̅ c̅] = 0
⇒ \(\) = 0
⇒ 2(-2t + 3) + 3(-t – 0) + 1(1 – 0) = 0
⇒ -4t + 6 – 3t + 1 = 0
⇒ -7t + 7 = 0
⇒ t = 1

Question 12.
If the vectors a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ + 2j̅ – 3k̅ and c̅ = 3i̅ + pj̅ + 5k̅ are coplanar then find p.
Answer:
Given a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ + 2j̅ – 3k̅, c̅ = 3i̅ + pj̅ + 5k̅
Since the vectors are coplanar then [a̅ b̅ c̅] = 0
⇒ \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & -3 \\
3 & \mathrm{p} & 5
\end{array}\right|\) = 0
= 2(10 + 3p) + 1(5 + 9) + 1(p – 6) = 0
⇒ 20 + 6p + 14 + p – 6 = 0
⇒ 7p + 28 = 0
⇒ p = -4

Question 13.
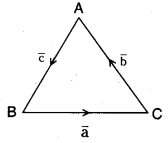
In ΔABC if \(\overline{\mathrm{B C}}\) = a̅, \(\overline{\mathrm{C A}}\) = b̅ and \(\overline{\mathrm{A B}}\) = c̅ then show that a̅ × b̅ = b̅ × c̅ = c̅ × a̅.
Answer:
a̅ + b̅ + c̅ = \(\overline{\mathrm{BC}}+\overline{\mathrm{CA}}+\overline{\mathrm{AB}}=\overline{\mathrm{BA}}+\overline{\mathrm{AB}}=\overline{0}\) (by vector addition)
∴ a̅ + b̅ = -c̅

⇒ a̅ × b̅ = c̅ × a̅ ………….(1) (∵ a̅ × a̅ = 0)
Again a̅ + b̅ = -c̅
(a̅ + b̅) × b̅ = -c̅ × b̅ ⇒ a̅ × b̅ + b̅ × b̅ = b̅ × c̅
⇒ a̅ × b̅ = b̅ × c̅ ……………..(2) (∵ b̅ × b̅ = 0)
∴ From (1) and (2); a̅ × b̅ = b̅ × c̅ = c̅ × a̅

Question 14.
Find a unit vector perpendicular to the plane determined by the points P(1, – 1, 2), Q(2, 0, – 1) and R (0, 2, 1).
Answer:
Let O be the origin.
\(\overline{\mathrm{OP}}\) = i̅ – j̅ + 2k̅, \(\overline{\mathrm{OQ}}\) = 2i̅ – k̅, \(\overline{\mathrm{OR}}\) = 2j̅ + k̅
\(\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}-\overline{\mathrm{OP}}\) = (2i̅ – k̅)-(i̅ – j̅ + 2k̅) = i̅ + j̅ – 3k̅
\(\overline{\mathrm{PR}}=\overline{\mathrm{OR}}-\overline{\mathrm{OP}}\) = (2j̅ + k̅) – (i̅ – j̅ + 2k̅) =-i̅ + 3j̅ – k̅

Now \(\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}\) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -3 \\
-1 & 3 & -1
\end{array}\right|\)
= i̅(-1 + 9) – j̅(-1 – 3) + k̅(3 + 1)
= 8i̅ + 4j̅ + 4k̅
= 4(2i̅ + j̅ + k̅)

\(|\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}|=4 \sqrt{4+1+1}\) = 4√6
∴ Unit vector perpendicular to the plane determined by the points P, Q and R is
= \(\pm \frac{(\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}})}{|\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}|}=\pm \frac{4(2 \overline{\mathrm{i}}+\overline{\mathrm{j}}+\overline{\mathrm{k}})}{4 \sqrt{6}}=\pm\left(\frac{2 \overline{\mathrm{i}}+\overline{\mathrm{j}}+\overline{\mathrm{k}}}{\sqrt{6}}\right)\)

Question 15.
If a̅, b̅ and c̅ are non coplanar vectors, then prove that the four points with position vectors 2a̅ + 3b̅ – c̅, a̅ – 2b̅ + 3c̅, 3a̅ + 4b̅ – 2c̅ and a̅ – 6b̅ + 6c̅ are coplanar.
Answer:
Suppose A, B, C, D are the given points with respect to a fixed origin ‘O’ and given that
\(\overline{\mathrm{OA}}\) = 2a̅ + 3b̅ – c̅,
\(\overline{\mathrm{OB}}\) = a̅ – 2b̅ + 3c̅ ,
\(\overline{\mathrm{OC}}\) = 3a̅ + 4b̅ – 2c̅ and
\(\overline{\mathrm{OD}}\) = a̅ – 6b̅ + 6c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = (a̅ – 2b̅ + 3c̅) – (2a̅ + 3b̅ – c̅) = – a̅ – 5b̅ + 4c̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = (3a̅ + 4b̅ – 2c̅) – (2a̅ + 3b̅ – c̅) = a̅ + b̅ – c̅
\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\) =(a̅ – 6b̅ + 6c̅) – (2a̅ + 3b̅ – c̅) = -a̅ – 9b̅ + 7c̅
∴ \(\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]=\left|\begin{array}{rrr}
-1 & -5 & 4 \\
1 & 1 & -1 \\
-1 & -9 & 7
\end{array}\right|\) [a̅ b̅ c̅]
=[-1(7 – 9)+ 5(7 – 1)+ 4 (-9 + 1)] [a̅ b̅ c̅]
= [-1(- 2) + 5 (6) + 4 (- 8)] [a b c]
= (2 + 30 – 32) [a̅ b̅ c̅] = 0
Hence the given points A, B, C, D are coplanar.

Question 16.
If a, b, c are three vectors, then show that a̅ × (b̅ × c̅) = (a̅ . c̅) b̅ – (b̅. c̅) a̅.
Answer:
Case – (i) : If a and b are parallel, then the result is true.
Case – (ii) : If a and b are not parallel, then suppose \(\overline{\mathrm{OA}}\) = a̅ and \(\overline{\mathrm{OB}}\) = b̅ with respect to an origin O. Since a and b are not parallel we have O, A, B are non collinear and hence determine a plane.
Let i̅ be a unit vector along OA and j̅ be a unit vector perpendicular to i̅ in XY plane, k̅ is a unit vector perpendicular to XZ plane such that i̅, j̅, k̅ form a right handed system and k̅ = i̅ × j̅

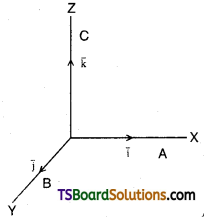
∴ a̅ = a₁i̅, b̅ = b₁i̅ + b₂j̅, c̅ = c₁i̅ + c₂j̅ + c₃k̅ for a₁, b₁, c₁, c₂, c₃, b₂ being scalars.
Since a̅ and b̅ are non parallel,
a̅ × b̅ = a₁i̅ × (b₁j̅ i̅ + b₂j̅) = a₁b₂k̅
∴ (a̅ × b̅) × c̅ = (a₁b₂k) × (c_1i̅  + c₂j + c₃k) = a₁b₂c₁j̅ – a₁b₂c₂i̅ ……………….(1)
(a̅.c̅)b̅ —(b̅.c̅)a̅ = a₁c₁ (b₁i̅ + b₂j̅) – (b₁c₁ + b₂c₂) a₁i̅ = a₁c₁b₂j̅ – a₁b₂c₂i̅ ……………. (2)
From (1) and (2),
∴ (a̅ × b̅) × c̅ = (a̅.c̅)b̅ – (b̅.c̅)a̅

Question 17.
Find the cartesian equation of the plane through the point A (2, – 1, – 4) and parallel to the plane 4x – 12y – 3z – 7 = 0.
Answer:
The equation of the parallel plane is 4x – 12y – 3z = p
It passes through A (2, – 1, – 4) then 4 (2) – 12 (- 1) – 3 (- 4) = p
⇒ 8 + 12 + 12 = p
⇒ p = 32
∴ The equation of the required plane is 4x – 12y – 3z = 32

Question 18.
Find the angle between the planes 2x – 3y – 6z = 5 and 6x + 2y – 9z = 4.
Answer:
Equation of the plane is 2x – 3y – 6z = 5 ⇒ r̅ . (2 i̅ – 3 j̅ – 6k̅) = 5 …………….(1)
Similarly 6x + 2y- 9z = 4 ⇒ r̅ . (6i̅ + 2 j̅ – 9k̅) = 4 ………………(2)
If the angle between the planes r̅. n̅₁ = d₁ and r̅.n̅₂ = d₂ is θ then
cos θ = \(=\frac{\overline{\mathrm{n}}_1 \cdot \overline{\mathrm{n}}_2}{\left|\overline{\mathrm{n}}_1\right|\left|\overline{\mathrm{n}}_2\right|}\)
= \(\frac{(2 \overline{\mathrm{i}}-3 \overline{\mathrm{j}}-6 \overline{\mathrm{k}}) \cdot(6 \overline{\mathrm{i}}+2 \overline{\mathrm{j}}-9 \overline{\mathrm{k}})}{\sqrt{4+9+36} \sqrt{36+4+81}}=\frac{12-6+54}{7(11)}\)
= \(\frac{60}{77}\)
∴ θ = cos^-1\(\left(\frac{60}{77}\right)\)

Question 19.
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3 j̅ – 5k̅. Find the vector c̅ such that a̅, b̅ and c̅ form the sides of a triangle.
Answer:
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅

∵ a̅, b̅, c̅ form the sides of a triangle a̅ + b̅ + c̅ = 0 (∵ \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CA}}\) = 0)
∴ c̅ = -a̅ – b̅ = -(2i̅ – j̅ + k̅) – (i̅ – 3j̅ – 5k̅) = -3i̅ + 4j̅ + 4k̅

Question 20.
Find the angle between the planes r̅ (2i̅ – j̅ + 2k̅) = 3 and r̅ . (3i̅ + 6j̅ + k̅) = 4. [Mar. ’15(TS)]
Answer:
If the angle between planes r̅.n̅₁ = p₁ and r̅.n̅₂ = p₂ is θ
then cos θ = \(\frac{\bar{n}_1 \cdot \bar{n}_2}{\left|\bar{n}_1\right| \cdot\left|\bar{n}_2\right|}=\frac{(2 \overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}) \cdot(3 \overline{\mathrm{i}}+6 \overline{\mathrm{j}}+\overline{\mathrm{k}})}{\sqrt{4+1+4} \sqrt{9+36+1}}\)
= \(\frac{6-6+2}{3 \sqrt{46}}=\frac{2}{3 \sqrt{46}}\)
∴ θ = cos^-1\(\left(\frac{2}{3 \sqrt{46}}\right)\)

Question 21.
If a̅ + b̅ + c̅ = 0, |a̅| = 3, |b̅| =5 and |c̅| = 7, then find the angle between a̅ and b̅.
Answer:
Given a̅ + b̅ + c̅ = 0 ⇒ c̅ =-(a̅ + b̅)
⇒ |c̅|² = (a̅ + b̅) = a̅² + b̅² + 2(a̅ b̅)
⇒ 49 = 9 + 25 + 2(a̅ b̅)
⇒ 2(a̅.b̅) = 49 – 34 = 15
⇒ a̅ . b̅ = \(\frac{15}{2}\)

If θ is the angle between a and b then cos θ = \(\frac{\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}}{|\overline{\mathrm{a}}||\overline{\mathrm{b}}|}=\frac{\frac{15}{2}}{3(5)}\)
= \(\frac{15}{2} \cdot \frac{1}{15}=\frac{1}{2}\)
∴ θ = cos^-1\(\left(\frac{1}{2}\right)=\frac{\pi}{3}\)
∴ Angle between a̅ and b̅ is \(\frac{\pi}{3}\)

Question 22.
If |a̅| = 2, |b̅| =3 and |c̅| = 4 and each of a̅, b̅, c̅ is perpendicular to the sum of the other two vectors, then find the magnitude of a̅ + b̅ + c̅.
Answer:
Given |a̅| = 2, |b̅| = 3 and |c̅| = 4
Since each of a̅, b̅, c̅ is perpendicular to the sum of other two vectors i.e., a̅ is perpendicular to b̅ + c̅.
.\a̅ – (b̅ + c̅) = 0
⇒ a̅ – b̅ + a̅ – c̅= 0
Similarly b̅ (c̅ + a̅) = 0
⇒ b̅ c̅ + b̅ a̅ = 0 and c̅.(a̅ + b̅) = 0
⇒ c̅.a̅ + c̅.b̅ = 0
Adding we get 2 [(a̅. b̅) + (b̅. c̅) + (c̅ . a̅)] = 0 ……………..(1)
Also (a̅ + b̅ + c̅) =|a̅|2 + |b̅|2 + |c̅|2 + 2(a̅b̅ + b̅c̅ + c̅a̅)
=4 + 9 + 16 + 2(a̅b̅ + b̅c̅ + c̅a̅)
= 4 + 9 + 16 + 2 (0) = 29
∴ |a̅ + b̅ + c̅| = \(\sqrt{29}\)

Question 23.
For any two vectors a̅ and b̅ show that |a̅ × b̅|2 = \(\overline{\mathrm{a}^2} \overline{\mathrm{b}^2}-(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}})^2\)
Answer:
We know that |a̅ × b̅| = |a̅| |b̅| sin θ, where ‘θ’ is the angle between a̅ and b̅.
Squaring on both sides |a̅ × b̅| = |a̅|² |b̅|² sin² θ = |a̅| |b̅| (1 – cos² θ)
= |a̅| |b̅̅| – |a̅|² |b̅|² cos² θ
= \(\overline{\mathrm{a}^2} \overline{\mathrm{b}^2}-(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}})^2\)

Question 24.
Find the area of the triangle formed by the two sides a̅ = i̅ + 2j̅ + 3k̅ and b̅ = 3i̅ + 5j̅ – k̅.
Answer:
Given a̅ = i̅ + 2 j̅ + 3k̅ and b̅ = 3 i̅ + 5 j̅ – k̅
Then a̅ × b̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 2 & 3 \\
3 & 5 & -1
\end{array}\right|\)
= i̅(-2 – 15) – j̅(-1 – 9) + k̅(5 – 6)
= -17i̅ + 10j̅ – k̅
Area of the triangle = \(\frac{1}{2}\)|a̅ × b̅| = \(\frac{1}{2} \sqrt{289+100+1}=\frac{1}{2} \sqrt{390}\)

Question 25.
For any vector g show that |a̅ × i̅|² + |a̅ × j̅|² +|a̅ × k̅|² = 2|a̅|².
Answer:
Let a̅ = xi̅ + yj̅ + zk̅, then a̅ × i̅ = -yk̅ + zj̅
|a̅ × i̅|² = y² + z²
Similarly |a̅ × j̅|² = z² + x² and |a̅ × k̅| = x²+ y²
∴ |a̅ × i̅|² + |a̅ × j̅|² + |a̅ × k̅|² = 2(x² + y² + z²) = 2|a̅|²

Question 26.
Find the area of the triangle having 3i̅ + 4j̅ and – 5i̅ + 7j̅ as two of its sides.
Answer:
Area of the triangle = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (3i̅ + 4 j̅) × (- 5i̅ + 7j̅) =-15(i̅ × i̅) – 20(j̅ × j̅) + 21(i̅ × j̅) + 28(j̅ × j̅)
= 20k̅ + 21k̅ = 41k̅
∴ Area of the ΔABC = \(\frac{1}{2}\)(41) = 20.5 sq. units

Question 27.
If a̅ = 2i̅ + j̅ – k̅, b̅ = -i̅ + 2j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅, then find (a̅ × b̅) . (b̅ × c̅).
Answer:
Given a̅ = 2i̅ + j̅ – k̅, b̅ = -i̅ + 2j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅
Then a̅ × b̅ = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
2 & 1 & -1 \\
-1 & 2 & -4
\end{array}\right|\)
= i̅(-4 + 2) – j̅(-8 – 1) + k̅(4 + 1) = -2i̅ + 9j̅ + 5k̅

b̅ × c̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{j}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
-1 & 2 & -4 \\
1 & 1 & 1
\end{array}\right|\)
= i̅(2 + 4) – j̅(-1 + 4) + k̅(-1 – 2) = 6i̅ – 3j̅ – 3k̅
(a̅ × b̅).(b̅ × c̅) = (-2i̅ + 9j̅ + 5k̅).(6i̅ – 3j̅ – 3k̅) = -12 – 27 – 15 = -54

Question 28.
Find the vector area and the area of the parallelogram having a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅ as adjacent sides.
Answer:
Given a̅ = i̅ + 2 j̅ – k̅ and b̅ = 2 i̅ – j̅ + 2k̅
Then the vector area of parallelogram = a̅ × b̅
∴ (a̅ × b̅) = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
1 & 2 & -1 \\
2 & -1 & 2
\end{array}\right|\)
= i̅(4 – 1) – j̅(2 + 2) + k̅(-1 – 4) = 3i̅ – 4j̅ – 5k̅
Magnitude of the area = \(\sqrt{9+16+25}=\sqrt{50}\) = 5√2 sq. units

Question 29.
If a̅ × b̅ = b̅ × c̅ ≠ 0, then show that a̅ + c̅ = pb̅, where p is some scalar.
Answer:
Consider (a̅ + c̅ – pb̅) × b̅ = (a̅ × b̅) + (c̅ × b̅) – p(b̅ × b̅) = (b̅ × c̅) – (b̅ × c̅) – p(0) = 0
∴ a̅ + c̅ – pb̅ = 0
⇒ a̅ + c̅ = pb̅

Question 30.
Let a and b be vectors, satisfying |a̅|=|b̅| = 5 and (a̅, b̅) = 45°. Find the area of the triangle having a̅ – 2b̅ and 3a̅ + 2b̅ as two of its sides. [May ’15(AP); Mar. ’07] [Mar ’18(AP)]
Answer:
Area of the triangle = \(\frac{1}{2}\)|(a̅ – 2b̅) × (3a̅ + 2b̅)| ……………(1)
Now |(a̅ – 2b̅) × (3a̅ + 2b̅)| = |3(a̅ × a̅) – 2(b̅ × a̅) – 6(b̅ × a̅) – 4(b̅ × b̅)|
= |2(a̅ × b̅) + 6(a̅ × b̅)| = |8(a̅ × b̅)| = 8|a||b| sin 45°
= 8(5)(5)\(\frac{1}{\sqrt{2}}\)
= 100√2

Question 31.
Let a̅ and b̅ be vectors, satisfying |a̅| = |b̅| = 5 and (a̅, b̅) = 45°. Find the area of the triangle having a̅ – 2b̅ and 3a̅ + 2b̅ as two of Its sides. [May ’15(AP); Mar. ’07] [Mar ’18(AP)]
Answer:
Area of the triangle = \(\frac{1}{2}\)|(a̅ – 2b̅) × (3a̅ + 2b̅)| ………….(1)
Now |(a̅ – 2b̅) × (3a̅ + 2b̅)| = |3(a̅ × a̅) – 2(b̅ × a̅) – 6(b̅ × a̅) – 4(b̅ × b̅)|
= |2(a̅ × b̅) + 6(a̅ × b̅)| = |8(a̅ × b̅)| = 8|a̅||b̅| sin 45
= 8(5)(5)\(\frac{1}{\sqrt{2}}\)
= 100√2

From (1), Area of the triangle = \(\frac{1}{2}\)(100)√2 = 50√2 sq.units

Question 32.
Find the volume of the tetrahedron having the edges i̅ + j̅ + k̅; i̅ – j̅ and i̅ + 2j̅ + k̅.
Answer:
Denoting the edges by a̅ ,b̅, c̅ of tetrahedron, then its volume is
= \(\frac{1}{6}\)[a̅ b̅ c̅] = \(\frac{1}{6}\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -1 & 0 \\
1 & 2 & 1
\end{array}\right|\) = \(\frac{1}{6}\) [1 (- 1) – 1 (1) + 1 (2 + 1)]
= \(\frac{1}{6}\) [-1 – 1 + 3] = \(\frac{1}{6}\) cubic units.

Question 33.
If a̅, b̅, c̅ are mutually perpendicular unit vectors, then find the value of [a̅ b̅ c̅]².
Answer:
Given a̅, b̅, c̅ are mutually perpendicular unit vectors.
We have |a̅| = |b̅| = |c̅| = 1 and taking a̅ = i̅, b̅ = j̅, c̅ = k̅
We have [a̅ b̅ c̅] = [i̅ j̅ k̅] = i̅ . (j̅ × k̅) = i̅ . i̅ = 1
∴ [a̅ b̅ c̅]² =1

Question 34.
Show that (a̅ + b̅) – (b̅ + c̅) × (c̅ + a̅) = 2 [a̅ b̅ c̅]
Answer:
(a̅ + b̅) . (b̅ + c̅) × (c̅ + a̅) = \(\left|\begin{array}{lll}
1 & 1 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1
\end{array}\right|\) [a̅ b̅ c̅]
= [1(1) – 1(-1)][a̅ b̅ c̅]
= 2[a̅ b̅ c̅]

Question 35.
Prove that a̅ × [a̅ × (a̅ × b̅)] = (a̅ . a̅) (b̅ × a̅)
Answer:
L.H.S = a̅ × [a̅ × (a̅ × b̅)] = a̅ × [(a̅ . b̅)a̅ – (a̅. a̅)b̅]
= (a̅ . b̅) (a̅ × a̅) – (a̅ . a̅) (a̅ × b̅)
= (a̅ . b̅) (0) – (a̅ a̅) (a̅ × b̅)
= (a̅.a̅)(b̅ × a̅) = R.H.S.

Question 36.
If a, b, c and d are coplanar vectors, then show that (a̅ × b̅) × (c̅ × d̅) = 0.
Answer:
Given a,b,c,d are coplanar vectors ⇒ a̅ × b̅ is perpendicular to the plane S.
In the similar way c̅ × d̅ is perpendicular to the plane S.
a̅ × b̅ and c̅ × d̅ are parallel vectors.
⇒ (a̅ × b̅) × (c̅ × d̅) = 0 (or) (a̅ × b̅) × (c̅ × d̅) = [a̅ c̅ d̅]b̅ – [b̅ c̅ d̅]a̅
= 0b̅ – 0a̅ = 0 (∵ a̅, b̅, c̅, d̅ are coplanar)

Question 37.
If a, b, c are non coplanar, then show that the vectors a̅ – b̅, b̅ + c̅, c̅ + a̅ are coplanar.
Answer:
Given that a̅, b̅, c̅ are non coplanar we have [a̅ b̅ c̅] ≠ 0
[a̅ – b̅ b̅ + c̅ c̅ + a̅] = [a̅ b̅ c̅] = [1 + 1(-1)][a̅ b̅ c̅] = 0
[a̅ b̅ c̅] = 0
∴ Vectors a̅ – b̅, b̅ + c̅, c̅ + a̅ are coplanar.

Question 38.
Let a̅, b̅ and c̅ be non coplanar vectors. If [2a̅ – b̅ + 3c̅, a̅ + b̅ – 2c̅, a̅ + b̅ – 3c̅] = λ [a̅ b̅ c̅] then find the value of λ.
Answer:
Given a̅, b̅, c̅ are non coplanar vectors
We have [a̅ b̅ c̅] ≠ 0
1 1 -2 [a̅ b̅ c̅] = [2 (- 3 + 2) + 1 (- 3 + 2) + 3 (1 – 1)] [a̅ b̅ c̅]
= [-2 – 1] [a̅ b̅ c̅] = -3[a̅ b̅ c̅]
Given [2a̅ – b̅ + 3c̅, a̅ + b̅ – 2c̅, a̅ + b̅ – 3c̅] = λ [a̅ b̅ c̅]
We have – 3 [a̅ b̅ c̅] = λ [a̅ b̅ c̅]
⇒ λ = -3

Question 39.
If a̅ = (1, – 1, – 6), b̅ = (1, – 3, 4) and c̅ = (2, – 5, 3), then compute a̅ × (b̅ × c̅)
Answer:
Given a̅ = (1, – 1, – 6), b̅ = (1, – 3, 4), c̅ = (2, – 5, 3)
Now b̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
1 & -3 & 4 \\
2 & -5 & 3
\end{array}\right|\)
= i̅(-9 + 20) – j̅(3 – 8) + k̅(-5 + 6)
= i̅(11) – 7(-5) + k(1) = 11i̅ + 5j̅ + k̅

a̅ × (b̅ × c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & -1 & -6 \\
11 & 5 & 1
\end{array}\right|\) = i̅(-1 + 30) – j̅ (1 + 66) + k̅(5 + 11)
= i̅(29) – j̅(67) + k̅(16)
= 29i̅ – 67j̅ + 16k̅

Question 40.
If |a̅| = 11, |b̅| = 23 and |a̅ – b̅| = 30, then find the angle between the vectors a̅, b̅ and also find |a̅ + b̅|.
Answer:
|a̅ – b̅| = 30 ⇒|a̅ – b̅|² = 900
⇒ |a̅|² + |b̅|² – 2(a̅.b̅) = 900
⇒ 121 + 529 – 2(a̅. b̅) = 900
⇒ 650 -2(a̅ . b̅) = 900
⇒ -2(a-b) = 250
⇒ -2 |a̅| |b̅| cos θ = 250
⇒ (-2)(253)cos θ = 25O
⇒ cos θ = \(\frac{125}{253}\)
⇒ θ = π – cos^-1\(\left(\frac{125}{253}\right)\)

Also |a̅ + b̅|² = |a̅|² + |b̅|² + 2(a̅.b̅) = 112 + 232 + 2|a̅||b̅|cos θ
= 121 + 529 + 2(11)(23)\(\left(\frac{-125}{253}\right)\) = 400
∴ |a̅ + b̅| = 20

Question 41.
Find λ in order that the four points A(3, 2, λ), B(4, λ, 5), C(4, 2, -2) and D(6, 5, – λ) be coplanar.
Answer:
\(\overline{\mathrm{OA}}\) = 3i̅ + 2j̅ + k̅; \(\overline{\mathrm{OB}}\) = 4i̅ + λj̅ + 5k̅; \(\overline{\mathrm{OC}}\) = 4i̅ + 2j̅ – 2k̅ and \(\overline{\mathrm{OD}}\) = 6i̅ + 5j̅ – k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = i̅ + (A – 2) j̅ + 4k̅;
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = i̅ – 3k̅;
\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\) = 3i̅ + 3j̅ – 2k̅

Given A, B, C, D are coplanar
⇒ \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}, \overline{\mathrm{AD}}\) are coplanar
⇒ \(\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]\) = 0
⇒ \(\left|\begin{array}{ccc}
1 & \lambda-2 & 4 \\
1 & 0 & -3 \\
3 & 3 & -2
\end{array}\right|\) = 0
⇒ 1 (9) – (λ – 2) (- 2 + 9) + 4(3) = 0
⇒ 21 – (λ – 2) (7) = 0
⇒ λ – 2 = 3
⇒ λ = 5

Question 42.
For any two vectors a̅ and b̅, show that (1 + |a̅|)² (1 + |b̅|)² = |1 – a̅. b̅|² + |a̅ + b̅ + a̅ × b̅|²
Answer:
Let |a̅| = a̅, |b̅| = b̅, (a̅, b̅) = θ.
LHS = (1 + a²) (1 + b²)
= 1 + a² + b² + a² b² …………..(1)
a̅. b̅ = |a̅||b̅| cos 9 = ab cos θ
|a̅ × b̅| = |a̅| |b̅| sin θ = ab sin θ
RHS = (1 – a . b)² + (a̅ + b̅ + a̅ × b̅)²
= 1 + (a̅ b̅)² – 2a̅ b̅ + a̅² + b̅² + |a̅ × b̅| + 2 a̅ . b̅ + 2(b̅ . a̅ × b̅) + 2(a̅ × b̅ . a̅)
= 1 + a̅²b̅² cos2 θ + a̅² + b̅² + a̅²b̅² sin2 θ + 0 + 0
= 1 + a̅²b̅² (cos2 θ + sin2 θ) + a̅² + b̅²
= 1 + a̅²b̅² (1) + a̅² +b̅²
= 1 + a̅²b̅² + a̅² + b̅²
= 1 + a̅² + b̅² + a̅²b̅²
= RHS.

Question 43.
If a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅, then find (a̅ + b̅) × (a̅ – b̅)
Answer:
Given a̅ = 2i̅ – 3j̅ + k̅
b̅ = i̅ + 4j̅ – 2k̅
Now
a̅ + b̅ = 2i̅ – 3j̅ + k̅ + i̅ + 4j̅ – 2k̅ = 3i̅ + j̅ – k̅
a̅ – b̅ = 2i̅ – 3j̅ + k̅ – i̅ – 4j̅ + 2k̅ = i̅ – 7j̅ + 3k̅
(a̅ + b̅) x (a̅ – b̅) = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -1 \\
1 & -7 & 3
\end{array}\right|\)
= i̅(3 – 7) – j̅(9 + 1) + k̅(-21 – 1)
= -4i̅ – 10j̅ – 22k̅

Question 44.
Show that the volume of a tetrahedron with a̅, b̅ and c̅ as coterminous edges is \(\frac{1}{6}\)|[a̅ b̅ c̅]|
Answer:
Let OABC be a tetrahedron and
\(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OC}}\) = c̅
Let V be the volume of the tetrahedron OABC. By definition the volume V is given by V = \(\frac{1}{3}\) (area of the base ΔOAB)
(Length of the perpendicular from C to the base ΔOAB)

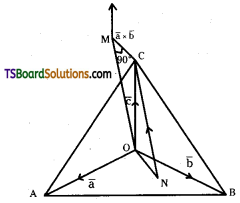
CN is the perpendicular from C to AOAB and CM is the perpendicular from C on to the supporting line of a̅ × b̅ so that CN = OM = Length of the projection of c onto a̅ × b̅.

Question 45.
Find the equation of the plane passing through the point (3, -2,1) and perpendicular to the vector (4, 7, -4).
Answer:
The vector equation of the plane is
[r̅ – (3 i̅ – 2 j̅ + k̅)j̅ . (4 i̅ + 7 j̅ – 4k̅) = 0
⇒ r̅ . (4i̅ + 7j̅ – 4k̅) – (12 – 14 – 4) = 0
⇒ r̅ . (4 i̅ + 7 j̅ – 4k̅) +6 = 0
The Cartesian equation is 4x + 7y – 4z + 6 = 0