TS Inter Second Year Maths 2A Probability Important Questions Long Answer Type

Students must practice these Maths 2A Important Questions TS Inter Second Year Maths 2A Probability Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter Second Year Maths 2A Probability Important Questions Long Answer Type

Question 1.
If one ticket is randomly selected from ticket numbers 1 to 30, then find the probability that the number on the ticket
is
I. a multiple of 5 or 7
II. a multiple of 3 or 5 [Mar. ’08]
Solution:
Let, S be the sample space.
No. of ways of drawing one ticket from 30 ticket
∴ n(S) = \({ }^{30} \mathrm{C}_1\) = 30
I) Let K be the event of getting a multiple of 5 then A = {5, 10, 15, 20, 25, 30}
∴ n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{30}=\frac{1}{5}\)
Let B be the event of getting a multiple of 7 then
B = {7, 14, 21, 28}
∴ n(B) = 4
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{30}=\frac{2}{15}\)
A ∩ R = getting a multiple of 5 and 9 = Φ
∴ n(A ∩ B) = 0
P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{0}{30}\) = 0
The probability that the number on the ticket is a multiple of 5 or 7.
According to addition theorem on probability,
P(A ∪ B) = P(A) + P(ß) – P(A ∩ B)
= \(\frac{1}{5}+\frac{2}{15}\) – 0
= \(\frac{3+2}{15}=\frac{5}{15}=\frac{1}{3}\).

II) Let A be the event of getting a multiple of 3 then
A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
∴ n(A) = 10
∴ P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{10}{30}=\frac{1}{3}\)
Let B be the event of getting a multiple of 5 then
B = {5, 10, 15, 20, 25, 30}
∴ n(B) = 6
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{6}{30}=\frac{1}{5}\)
A ∩ B is the event getting a multiple of 5 and 3 then A ∩ B = {15, 30}
∴ n(A ∩ B) = 2
∴ P(A ∩ B) = \(\frac{\mathrm{n}(\mathrm{A} \cap \mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{2}{30}=\frac{1}{15}\)
The probability that the number on the ticket is a multiple of 3 or 5. According to addition theorem on probability.
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{1}{3}+\frac{1}{5}-\frac{1}{15}\)
= \(\frac{5+3-1}{15}=\frac{7}{15}\).

Question 2.
The probabilities of three events A, B, C are such that P(A) = 0.3, P(B) = 0.4, P(C) = 0.8, P(A ∩ B) = 0.08, P(A ∩ C) = 0.28, P(A ∩ B ∩ C) = 0.09 and P(A ∪ B ∪ C) = 0.75. Show that P(B ∩ C) lies in the interval [0.23, 0.48]. [Board Paper]
Solution:
Given that,
P(A) = 0.3, P(B) = 0.4, P(C) = 0.8
P(A ∩ B) = 0.08, P(A ∩ C) = 0.28
P(A ∩ B ∩ C) = 0.09, and P(A ∪ B ∪ C) ≥ 0.75
Now,
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
= 0.3 + 0.4 + 0.8 – 0.08 – P(B ∩ C) – 0.28 + 0.09
= – 0.27 + 1.5 – P(B ∩ C)
= 1.23 – P(B ∩ C)
Since, P(A ∪ B ∪ C) ≥ 0.75
⇒ 0.75 ≤ P(A ∪ B ∪ C) ≤ 1
⇒ 0.75 ≤ 1.23 – P(B ∩ C) ≤ 1
⇒ 0.75 – 1.23 ≤ P(B ∩ C) ≤ 1 – 1.23
⇒ -0.48 ≤ – P(B ∩ C) ≤ – 0.23
⇒ 0.48 ≥ P(B ∩ C) ≥ 0.23
⇒ 0.23 ≤ P(B ∩ C) ≤ 0.48
∴ P(B ∩ C) c [0.23, 0.48]
∴ P(B ∩ C) lies in the interval [0.23, 0.48].

Question 3.
The probabilities of 3 mutually exclisive events are respectively given as \(\frac{1+3 \mathbf{P}}{3}, \frac{1-\mathbf{P}}{\mathbf{4}}, \frac{\mathbf{1 – 2 P}}{\mathbf{2}}\). Prove that \(\frac{1}{3}\) ≤ p ≤ \(\frac{1}{2}\)
Solution:
Suppose, A, B, C are exclusive event such that
P(A) = \(\frac{1+3 p}{3}\)
P(B) = \(\frac{1-p}{3}\)
P(C) = \(\frac{1-2 p}{2}\)
We know that
0 ≤ P(A) ≤ 1
0 ≤ \(\frac{1+3 \mathrm{p}}{3}\) ≤ 1
0 ≤ 1 + 3p ≤ 3
0 ≤ 1 ≤ 3p ≤ 3 – 1
– 1 ≤ 3p ≤ 2
\(\frac{-1}{3} \leq p \leq \frac{2}{3}\) …………….(1)
0 ≤ P(B) ≤ 1
0 ≤ \(\frac{1-p}{4}\) ≤ 1
0 ≤ 1 – p ≤ 4
0 – 1 ≤ 1 – p – 1 ≤ 4 – 1
– 1 ≤ – p ≤ 3
1 ≥ p ≥ – 3
– 3 ≤ p ≤ 1 ……………(2)
0 ≤ \(\frac{1-2 p}{2}\) ≤ 1
0 ≤ 1 – 2p ≤ 2
o – 1 ≤ 1 – 2p – 1 ≤ 2 – 1
– 1 ≤ – 2p ≤ 1
\(+\frac{1}{2}\) p ≥ \(\frac{1}{2}\)
\(\frac{1}{2}\) ≤ p ≤ \(\frac{1}{2}\)
Since, A, B, C are mutually exclusive events then 0 ≤ P(A ∪ B ∪ C) ≤ 1
0 ≤ P(A) + P(B) + P(C) ≤ 1
0 ≤ \(\frac{1+3 p}{3}+\frac{1-p}{4}+\frac{1-2 p}{2}\) ≤ 1
0 ≤ \(\frac{4+12 p+3-3 p+6-12 p}{12}\) ≤ 1
0 ≤ \(\frac{13-3 p}{12}\) ≤ 1
0 ≤ 13 – 3p ≤ 12
0 – 13 ≤ – 3p ≤ 12 – 13
– 13 ≤ – 3p ≤ – 1

Question 4.
State and prove addition theorem on probability [May ‘14, ‘12, ‘09, ‘08, ’07, ‘06, ‘05, Mar. ’14. ‘11. ‘07; AP – Mar. ‘18. ‘17; TS – Mar.’18. May ‘16]
Solution:
Addition theorem on probability:
If A, B are two events in a sample space, S then P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

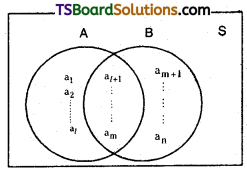
Proof:
In a sample space
A = {a₁, a₂, …………………. a₁, a₁₊₁, ……………. a_m)
B = {a₁₊₁ ……… am, a_m+1 …………………… a_n}
A ∩ B = {a₁₊₁, ………………., a_m}
A ∪ B = {a₁, a₂, ……….. a₁, a₁₊₁, a_m, a_m+1, …………..a_m}
According to definition of probability
P(A) = \(\sum_{i=1}^m\) P(a_i)
P(B) = \(\sum_{\mathbf{i}=l+1}^{\mathrm{n}}\) P(a_i)
P(C) = \(\sum_{\mathbf{i}=l+1}^{\mathrm{n}}\) P(a_i)

Question 5.
If A, B, C are 3 independent events of an experiment such that \(P\left(A \cap B^C \cap C^C\right)=\frac{1}{4}\), \(P\left(A^C \cap B \cap C^C\right)=\frac{1}{8}\), \(P\left(A^C \cap B \cap C^C\right)=\frac{1}{4}\) then P(A), P(B) and P(C). [Mar. ’10, AP – May 2016; TS – Mar. 2015]
Solution:
Given that,
A, B, C are three independent events then \(A^{\mathrm{C}}, \mathrm{B}^{\mathrm{C}}, \mathrm{C}^{\mathrm{C}}\) are also independent events.

Question 6.
State and prove multiplication theorem on probability. [TS – May ’15, May ’10, Mar. ’04]
Solution:
Multiplication theorem of probability: (or) Theorem of compound probability:
Let A, B be two events in a sample s pace, S such that P(A) ≠ 0, P(B) ≠ 0 then
I) P(A ∩ B) = P(A). \(\mathrm{P}\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\)
II) P(A ∩ B) = P(B). \(\mathrm{P}\left(\frac{\mathrm{A}}{\mathrm{B}}\right)\)
Proof:
Let, n(A), n(B), n(A ∩ B), n(S) be the number of sample points in A, B, A ∩ B, S respectively.
Then,

Question 7.
State and prove Baye’s theorem on probability,
Statement: If A₁, A₂, ………….., A_n, are mutually exclusive and exhaustive events in a sample space, S such that P(A₁) > 0 for i = 1, 2, …, n and E is any event with P(E) > 0 then \(P\left(\frac{A_K}{E}\right)=\frac{P\left(A_K\right) \cdot P\left(\frac{E}{A_K}\right)}{\sum_{i=1}^n P\left(A_i\right) P\left(\frac{E}{A_i}\right)}\) for K = 1, 2, ………….., n. [Mar. 12, ‘09, May ‘05 AP – Mar. May, ’15, ’16, TS – Mar. ‘17, ‘16, AP – Mar. 2019]
Solution:
Proof :
Since, A₁, A₂, …………….. A_n are mutually exclusive and exhaustive events in a sample space, S it follows that \(\bigcup_{i=1}^n\) A_i = S and
A₁, A₂, ………….. A_n are mutually disjoint.
Now,
E ∩ A₁, E ∩ A₂, ……………….. E ∩ A_n are mutually disjoint.
∴ P(E) = P(E ∩ S)

Question 8.
Suppose that an urn B₁ contains two white and 3 black balls and another urn B₂ contains 3 white and 4 black balls. One urn is selected at random and a ball is drawn from it. If the ball drawn is found black, find the pobability that the urn choosen was B₁.
Solution:
Let E₁, E₂ denote the events of selecting mens B₁ and B₂ respectively then
P(E₁) = \(\frac{1}{2}\),
P(E₂) = \(\frac{1}{2}\)
Let B denote the event that the ball choosen from the selected men is black then

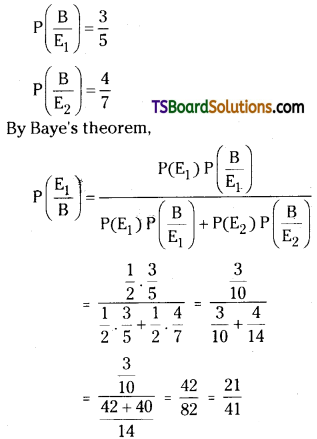
Question 9.
Three boxes B₁, B₂ and B₃ contain balls with different colours as shown below.

A die is thrown. B₁ is chosen if either 1 or 2 turns up. B₂ is chosen If 3 or 4 turns up and B₃, is chosen if 5 or 6 turns up. Having chosen a box In this way, a ball is choosen at random from this box. If the ball drawn Is found to be red, find the probability that it is drawn fron box B₂.
Solution:
Let E₁, E₂, E₃ denote the events of selecting boxes B₁, B₂, B₃ respectively.
∴ P(E₁) = \(\frac{2}{6}=\frac{1}{3}\)
P(E₂) = \(\frac{2}{6}=\frac{1}{3}\)
P(E₃) = \(\frac{2}{6}=\frac{1}{3}\)
Let f denote the event that the ball choosen from the selected box is red.

Question 10.
An urn contains ‘w’ white halls and ‘b’ black balls. Two players Q and R alternatively draw a ball with replacement from the urn. The player that draws a white ball first wins the game. If Q begins the game, find the probability of his winning the game.
Solution:
Let w denote the event of drawing a white ball in any draw then
P(w) = \(\frac{w_{C_1}}{(w+b)_{C_1}}=\frac{w}{w+b}\)
Let B denote the event of drawing a black ball in any draw then
P(B) = \(\frac{\mathrm{b}_{\mathrm{C}_1}}{(\mathrm{w}+\mathrm{b})_{\mathrm{C}_1}}=\frac{\mathrm{b}}{\mathrm{w}+\mathrm{b}}\)
The probability of Q wins the game.
= P(w ∪ BBw ∪ BBBBw ∪ ……………. )
= P(w) + P(BBw) + P(BBBB)w) + ……………..
= P(w) + P(B)P(B)P(w) + P(B) P(B) P(B) P(B) P(w) + …………….
= P(w) [1 [P(B)²+ [P(B)]⁴ + ……………….]

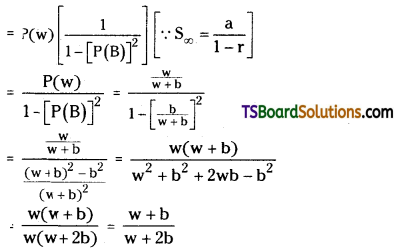
Question 11.
Three urns have the following composition of balls:
urn I : 1 white, 2 black
urn II: 2 white, 1 black
urn III: 2 white, 2 black
One of the urns is selected at random and a ball is drawn. it turns out of two be white. Find the probability that It came
from urn III. [AP – Mar. 2017] [May ’13]
Solution:
Let, A₁, A₂, A₃ be the events of selecting urn – I, urn – II, urn – III respectively then
P(A₁) = \(\frac{1}{3}\),
P(A₂) = \(\frac{1}{3}\),
P(A₃) = \(\frac{1}{3}\)
Now A₁, A₂, A₃ are mutually exclusive and exhaustive events.
Let E be the event of drawing a white ball from the selected urn.

Question 12.
A person is known to speak truth 2 out of 3 times. He throws a die and reports that it is 1. Find the probability that it is actually 1.
Solution:
Let, A be the event that 1 occurs when a die is thrown.
∴ P(A) = \(\frac{1}{6}\)
Let, E be the event that the man reports that it is 1. Since, the man speaks the truth 2 out of 3 times.

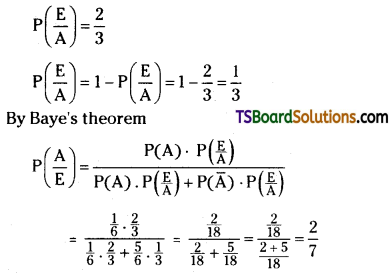
Question 13.
Three boxes numbered I, II, III contain the balls as follows:

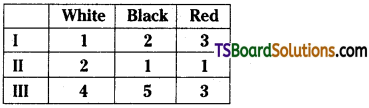
One box is randomly selected and a ball is drawn from it. If the ball is red, then find the probability that It Is from Box – II. [TS. Mar. 2019]
Solution:
Let A₁, A₂, A₃ be the events of drawing a ball from the box numbered I, II, III respectively and E be the event of drawing a red ball from the selected box.
P(A₁) = \(\frac{1}{3}\),
P(A₂) = \(\frac{1}{3}\),
P(A₃) = \(\frac{1}{3}\) and
A₁, A₂, A₃ are mutually exclusive and exhaustive events.
P(E/A₁) = \(\frac{3}{6}=\frac{1}{2}\)
P(E/A₂) = \(\frac{1}{4}\)
P(E/A₃) = \(\frac{3}{12}=\frac{1}{4}\)
P(A₂/E) = P(A₂) . P(E/A₂) P(A₁) . P(E/A₁) + P(A₂) . P(E/A₂) + P(A₃) P(E/A₃)
= \(\frac{\frac{1}{3} \times \frac{1}{4}}{\frac{1}{3} \times \frac{1}{2}+\frac{1}{3} \times \frac{1}{4}+\frac{1}{3} \times \frac{1}{4}}\) = \(\frac{\frac{1}{4}}{\frac{1}{2}+\frac{1}{4}+\frac{1}{4}}=\frac{1}{4}\)