Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Product of Vectors Important Questions Short Answer Type to help strengthen their preparations for exams.
TS Inter 1st Year Maths 1A Product of Vectors Important Questions Short Answer Type
Question 1.
Prove that angle in a semi-circle is a right angle by using vector method. [MAR ’13, ’08, ’99]
Answer:
Let AB be a diameter of a circle with centre O.
Let OA = a, then OB = -a
Let P be a point on the circle and OP = r
OA = OB = OP
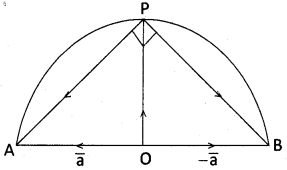

∠APB = 90°
∴ Angle in a semicircle is 90°.
Question 2.
If P, Q, R and S are points whose position vectors are i̅ – k̅, -i̅ + 2j̅, 2i̅ – 3k̅ and 3i̅ – 2j̅ – k̅ respectively, then find the component of RS on PQ. [Mar. ’98]
Answer:
The position vectors of the points P, Q, R and S with respect to the origin ‘O’ are
\(\overline{\mathrm{OP}}\) = i̅ – k̅,
\(\overline{\mathrm{OQ}}\) = -i̅ + 2j̅,
\(\overline{\mathrm{OR}}\) = 2i̅ – 3k̅,
\(\overline{\mathrm{OS}}\) = 3i̅ – 2j̅ – k̅
Now \(\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}-\overline{\mathrm{OP}}\) = -i̅ + 2j̅ -i̅ + k̅ = -2i̅ + 2j̅ + k̅
\(\overline{\mathrm{RS}}=\overline{\mathrm{OS}}-\overline{\mathrm{OR}}\) = 3i̅ – 2j̅ – k̅ – 2i̅ + 3k̅ = i̅ – 2j̅ + 2k̅

Question 3.
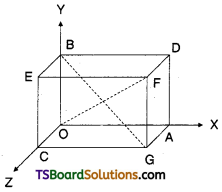
Prove that the angle ‘θ’ between any two diagonals of cube is given by cos θ = \(\frac{1}{3}\). [Mar ’12, ’11, ’10; Mar. ’10]
Answer:
Let \(\overline{\mathrm{OA}}\) = i̅, \(\overline{\mathrm{Ob}}\) = j̅ ,\(\overline{\mathrm{Oc}}\) = k̅
Let OA = OB = OC = 1 unit
In a cube, diagonals are OF, CD, BG, AE

![]()
Question 4.
Show that the points (5, – 1, 1), (7, – 4, 7), (1, – 6, 10) and (- 1, – 3, 4) are the vertices of a rhombus by vectors. [Mar. ’13]
Answer:
Let A(5, – 1, 1), B(7, – 4, 7), C(1, – 6, 10) and D(- 1, – 3, 4) are the given points.
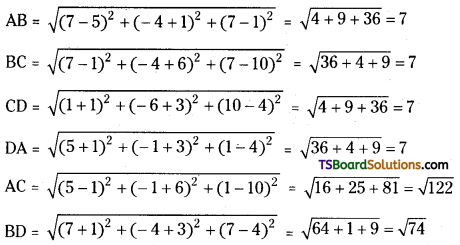
∴ AB = BC = CD = DA = 7 units and AC ≠ BD.
∴ A, B, C, D are the points which are the vertices of a rhombus.
Question 5.
Find the area of the triangle whose vertices are A(1, 2, 3), B(2,3, 1) and C(3,1, 2). [Mar. ’14, ’06]
Answer:
Let the position vectors of A, B, C with respect to the origin are
\(\overline{\mathrm{OA}}\) = i̅ + 2j̅ + 3k̅, \(\overline{\mathrm{OB}}\) = 2i̅ + 3j̅ + k̅, \(\overline{\mathrm{OC}}\) = 3i̅ + j̅ + 2k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = 2i̅ + 3j̅ + k̅ – i̅ – 2j̅ – 3k̅ = i̅ + j̅ – 2k̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = 3i̅ + j̅ + 2k̅ – i̅ – 2j̅ – 3k̅ = 2i̅ – j̅ – k̅
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = \(\left|\begin{array}{ccc}
\overline{\mathbf{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -2 \\
2 & -1 & -1
\end{array}\right|\)
= i̅(-1 -2) – j̅(-1 + 4) + k̅(-1-2) = -3i̅ -3j̅ – 3k̅
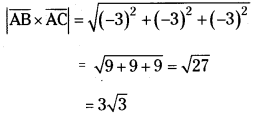
∴ The area of triangle whose vertices are A, B, C is \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\) = \(\frac{3 \sqrt{3}}{2}\)
Question 6.
If a̅ + b̅ + c̅ = 0, then prove that a̅ × b̅ = b̅ × c̅ = c̅ × a̅. [Mar. ’03; May ’98]
Answer:
Given a̅ + b̅ + c̅ = 0
⇒ a̅ = -b̅ – c̅
⇒ a̅ × b̅ = (-b̅ – c̅) × b̅
= -(b̅ × b̅) – (c̅ × c̅)
= -0 + b̅ × c̅
= a̅ × b̅ = b̅ × c̅ ………………(1)
⇒ a̅ + b̅ + c̅ = 0
b̅ = -a̅ – c̅
⇒ b̅ × c̅ = (-a̅ – c̅) × c̅ =-(a̅ × c̅) – (c̅ × b̅) = c̅ × a̅ – 0
b̅ × c̅ = c̅ × a̅ ……………………..(2)
From (1) & (2) ⇒ a̅ × b̅ = b̅ × c̅ = c̅ × a̅
Question 7.
Find the unit vector perpendicular to the plane passing through the points (1, 2, 3), (2,-1,1) and (1,2,-4). [Mar. ’17(AP) ’05; May ’10]
Answer:
Let the position vectors of the points A, B, C with respect to the origin ‘O’ are
\(\overline{\mathrm{OA}}\) = i̅ + 2 j̅ + 3k̅; \(\overline{\mathrm{OB}}\) = 2 i̅ – j̅ + k̅; \(\overline{\mathrm{OC}}\) = i̅ + 2 j̅ – 4k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = 2i̅ – j̅ + k̅ – i̅ – 2j̅ – 3k̅ = i̅ – 3 j̅ – 2k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = i̅ + 2j̅ – 4k̅ – i̅ – 2j̅ – 3k̅
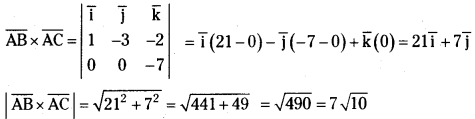
The unit vector perpendicular to the plane passing through the points A, B and C is
\(\pm \frac{(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}})}{|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|}=\pm \frac{(21 \overline{\mathrm{i}}+7 \overline{\mathrm{j}})}{7 \sqrt{10}}=\pm \frac{(3 \overline{\mathrm{i}}+\overline{\mathrm{j}})}{\sqrt{10}}\)
Find a unit vector perpendicular to the plane determined by the points P(1, – 1, 2), Q(2, 0, – 1) and R (0, 2, 1).
Answer:
±\(\frac{1}{\sqrt{6}}\)(2i̅ + j̅ + k̅)
Question 8.
If a̅ = 2i̅ + 3j̅ + 4k̅, b̅ = i̅ + j̅ – k̅ and c̅ = i̅ – j̅ + k̅, then compute a̅ × (b̅ × c̅) and verify that it is perpendicular to a̅. [Mar. ’19(TS); May ’06; May ’03]
Answer:
Given vectors are a̅ = 2i̅ + 3j̅ + 4k̅, b̅ = i̅ + j̅ – k̅, c̅ = i̅ – j̅ + k̅
b̅ × c̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -1 \\
1 & -1 & 1
\end{array}\right|\)
= i̅(1 – 1) -j̅(1 + 1) + k̅(-1- 1) = 2i̅ – 2k̅
a̅ × (b̅ × c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 3 & 4 \\
0 & -2 & -2
\end{array}\right|\)
= i̅(-6 + 8) – j̅(-4 – 0) + k̅(-4-0)
= 2i̅ + 4j̅ – 4k̅
Now [a̅ × (b̅ × c̅)].a̅ = (2i̅ + 4j̅ – 4k̅).(2i̅ + 3j̅ + 4k̅) = 4 + 12 – 16 = 0
a̅ × (b̅ × c̅) is perpendicular to a̅.
![]()
Question 9.
For any four vectors a, b, c and d show that (a̅ × b̅) . (c̅ × d̅) = \(\left|\begin{array}{cc}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|\) and in particular \((\overline{\mathrm{a}} \times \overline{\mathrm{b}})^2=\overline{\mathrm{a}^2} \overline{\mathrm{b}^2}-(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}})^2\). [Mar. ’02, ’00]
Answer:
LHS = (a̅ × b̅). (c̅ × d̅) = a̅. (b̅ × (c̅ × d̅)) = a̅. [(b̅. d̅) c̅ – (b̅. c̅) d̅]
= (a̅ . c̅)(b̅ . d̅) – (a̅ . d̅)(b̅ . c̅) = \(\left|\begin{array}{cc}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|\)
In the above formula if c̅ = a̅ and d̅ = b̅, then
(a̅ × b̅) . (c̅ × d̅) = \(\left|\begin{array}{cc}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|\) = (a̅.a̅)(b̅.b̅) – (a̅.b̅)(a̅.b̅) = \(\overline{\mathrm{a}^2} \overline{\mathrm{b}^2}-(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}})^2\)
Question 10.
Let a̅, b̅ and c̅ be unit vectors such that b is not parallel to c and a̅ × (b̅ × c) = \(\frac{1}{2}\) b̅. Find the angles made by a̅ with each of b̅ and c̅. [May ’01]
Answer:
Since a̅, b̅ and c̅ be unit vectors then |a̅| = 1, |b̅| = 1, |c̅| = 1
Given a̅ × (b̅ × c̅) = -b̅
⇒ (a̅.c̅)b̅ – (a̅.b̅)c = \(\frac{1}{2}\)b̅
Since b̅ and c̅ are non-collinear vectors equating corresponding coefficients on both sides.
a̅.c̅ = \(\frac{1}{2}\)
|a||c| cos (a, c) = \(\frac{1}{2}\), -(a̅.b̅) = 0
1.1.cos(a̅, c̅) = \(\frac{1}{2}\), a̅.b̅ = 0
cos(a̅,c̅) = \(\frac{1}{2}\), a̅ ⊥ b̅
(a̅, c̅) = 60°, (a̅, b̅) = 90°
Question 11.
Let a̅ = i̅ + j̅ + k̅, b̅ = 2i̅ – j̅ + 3k̅, c = i̅ – j̅ and d̅ = 6i̅ + 2j̅ + 3k̅ . Express d̅ in terms of b̅ × c̅, c̅ × a̅ and a̅ × b̅. [May ’12]
Answer:
Given a̅ = i̅ + j̅ + k̅, b̅ = 2i̅ – j̅ + 3k̅, c̅ = i̅ – j̅, d̅ = 6i̅ + 2j̅ + 3k̅
= 1 (0 + 3) – 1 (0 – 3) + 1(-2 + 1) = 3 + 3 – 1 = 5
Now, d̅. a̅ = (6 i̅ + 2 j̅ + 3k̅). (i̅ + j̅ + k̅) = 11
d̅.b̅ = (6i̅ + 2j̅ + 3k̅).(2i̅ – j̅ + 3k̅) =19
d̅.c̅ = (6i̅ + 2j̅ + 3k̅).(i̅ – j̅) = 4
Take d̅ = x(b̅ x c̅) + y(c̅ x a̅) + z(a̅ x b̅), then we have x = \(\frac{\overline{\mathrm{d}} \cdot \overline{\mathrm{a}}}{\left[\begin{array}{lll}
\overline{\mathrm{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}}
\end{array}\right]}\), y = \(\frac{\overline{\mathrm{d}} \cdot \overline{\mathrm{b}}}{\left[\begin{array}{lll}
\overline{\mathrm{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}}
\end{array}\right]}\), z = \(\frac{\overline{\mathrm{d}} \cdot \overline{\mathrm{c}}}{\left[\begin{array}{lll}
\overline{\mathrm{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}}
\end{array}\right]}\)
∴ x = \(\frac{11}{5}\), y = \(\frac{19}{5}\), z = \(\frac{4}{5}\)
d̅ = \(\frac{11}{5}\) (3i̅ + 3j̅ – k̅) + \(\frac{19}{5}\)(-i̅ – j̅ + 2k̅) + \(\frac{4}{5}\)(4i̅ – j̅ – 3k̅)
Question 12.
For any four vectors a̅, b̅, c̅ and d̅, show that
(i) (a̅ × b̅) × (c̅ × d̅) = [a̅ c̅ d̅] b̅ – [b̅ c̅ d̅] a̅ and
(ii) (a̅ × b̅) × (c̅ × d̅) = [a̅ b̅ d̅]c̅ – [a̅ b̅ c̅]d̅. [Mar. ’18(AP); May ’99]
Answer:
(i) (a̅ × b̅) × (c̅ × d̅) = [(c̅ × d̅).a̅]b̅ – [(c̅ × d̅).b̅]a̅ = [a̅.(c̅ × d̅)]b̅ – [b̅.(c̅ × d̅)]a̅ = [a̅ c̅ d̅] b̅ – [b̅ c̅ d̅] a̅
(ii) (a̅ × b̅) × (c̅ × d̅) = [(a̅ × b̅). d̅]c̅ – [(a̅ × b̅). c̅]d̅ = [a̅ b̅ d̅]c̅ – [a̅ b̅ c̅]d̅
Question 13.
a, b, c are non-zero vectors and a is perpendicular to both b̅ and c̅. If |a̅| = 2, |b̅| = 3, |c̅| = 4 and (b̅, c̅) = \(\frac{2 \pi}{3}\), then find |[a̅ b̅ c̅]|. [May ’08]
Answer:
Given |a̅| = 2, |b̅| = 3, |c̅| = 4 and (b̅, c̅) = \(\frac{2 \pi}{3}\)
a is perpendicular to both b̅ and c̅.
Now b̅ × c̅ is a vector perpendicular to both b̅ & c̅.
a̅ is parallel to b̅ × c̅ (a̅, b̅ × c̅) = 0° or 180°
Now [a̅ b̅ c̅] = a̅. (b̅ × c̅) = |a̅| |b̅ × c̅| cos (a̅, b̅ × c̅) = |a̅| |b̅| |c̅| sin (b̅, c̅). cos (a̅, b̅ × c̅)
= 2.3.4.sin \(\frac{2 \pi}{3}\) . cos(0° or 180°) = 24. \(\frac{\sqrt{3}}{2}\)(±1) = 12√3 = |[a b c]| = 12√3
![]()
Question 14.
If [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅] = [a̅ b̅ c̅], then show that the points with position vectors a̅, b̅, c̅ and d̅ are coplanar. [Mar ’14; Mar. ’00]
Answer:
Let the position vectors of the points A, B, C and D with respect to the origin O’ are \(\overline{\mathrm{OA}}\) = a, \(\overline{\mathrm{OB}}\) = b, \(\overline{\mathrm{OC}}\) = c, \(\overline{\mathrm{OD}}\) = d.
Given [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅] = [a̅ b̅ c̅] ……………………(1)
Now \([\overline{\mathrm{AB}} \overline{\mathrm{AC}} \overline{\mathrm{AD}}]=[\overline{\mathrm{OB}}-\overline{\mathrm{OA}} \overline{\mathrm{OC}}-\overline{\mathrm{OA}} \overline{\mathrm{OD}}-\overline{\mathrm{OA}}]\)
= [b̅ – a̅ c̅ – a̅ d̅ – a̅]
= (b̅ – a̅). [(c̅ – a̅) × (d̅ – a̅)] (b̅ – a̅).[c̅ × d̅ – c̅ × a̅ – a̅ × d̅ + a̅ × a̅]
= (b̅ – a̅).[c̅ × d̅ + a̅ × c̅ + d̅ × a̅ + 0]
= b̅. (c̅ × d̅) + b̅. (a̅ × c̅) + b̅. (d̅ × a̅) – a̅ . (c̅ × d̅) – a̅. (a̅ × c̅) – a̅. (d̅ × a̅)
= [b̅ c̅ d̅] + [b̅ a̅ c̅] + [b̅ d̅ a̅] – [a̅ c̅ d̅] – [a̅ a̅ c̅] – [a̅ d̅ a̅]
= [b̅ c̅ d̅] – [a̅ b̅ c̅] – [b̅ a̅ d̅] + [c̅ a̅ d̅] – 0 – 0
= [b̅ c̅ d̅] – [a̅ b̅ c̅] + [a̅ b̅ d̅] + [c̅ a̅ d̅]
= [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅] – [a̅ b̅ c̅]
= [a̅ b̅ c̅] – [a̅ b̅ c̅] = 0 (from (1))
∴ The vectors AB, AC, AD are coplanar.
∴ The four points A, B, C and D are coplanar.
Question 15.
Find the volume of the tetrahedron whose vertices are (1, 2, 1), (3, 2, 5), (2, – 1, 0) and (- 1, 0, 1). [Mar. ’15(TS); May ’07; Mar. ’04]
Answer:
Let the position vectors of the points A, B, C and D with respect to the origin ‘O’ are
\(\overline{\mathrm{OA}}\)= i̅ + 2j̅ + k̅, \(\overline{\mathrm{OB}}\) = 3i̅ +2j̅ +5k̅, \(\overline{\mathrm{OC}}\) = 2i̅ – j̅, \(\overline{\mathrm{OD}}\) = -i̅ + k̅
Now \(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\)A
= 3i̅ + 2j̅ + 5k̅ – i̅ – 2j̅ – k̅
= 2i̅ + 4k̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\)
=2i̅ – j̅ – i̅ – 2j̅ – k̅
= i̅ – 3j̅ – k̅
\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\)
= -i̅ + k̅ – i̅ – 2j̅ – k̅
= -2i̅ – 2j̅
The volume of the tetrahedron whose vertices are A, B, C and D is \(\frac{1}{6}\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]\)
\(\frac{1}{6}\left|\begin{array}{ccc}
2 & 0 & 4 \\
1 & -3 & -1 \\
-2 & -2 & 0
\end{array}\right|\)
= \(\frac{1}{6}\)|2(0 – 2) – 0(0 – 2) + 4(-2 – 6)|
= \(\frac{1}{6}\)|-4-32|
= \(\frac{36}{6}\) = 6
∴ Volume = 6 cubic units.
Question 16.
Prove that the four points 4i̅ + 5j̅ + k̅,-(j̅ + k̅), 3i̅ + 9j̅ + 4k̅ and -4i̅ + 4j̅ + 4k̅ are coplanar. [Mar. ’99]
Answer:
Let the position vectors of the points A, B, C and D with respect to the origin ‘O’ are \(\overline{\mathrm{OA}}\) = 4i̅ + 5j̅ + k̅,\(\overline{\mathrm{OB}}\) = -(j̅ + k̅), \(\overline{\mathrm{OC}}\) = 3i̅ + 9j̅ + 4k̅,\(\overline{\mathrm{OD}}\) = -4i̅ + 4j̅ + 4k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = -j̅ – k̅ – 4 i̅ – 5j̅ – k̅ = -4i̅ – 6j̅ – 2k̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = 3i̅ + 9j̅ + 4k̅ – 4i̅ – 5j̅ – k̅ = -i̅ + 4j̅ + 3k̅
\(\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}\) = – 4i̅ + 4j̅ + 4k̅ – 4i̅ – 5j̅ – k̅ = -8i̅ – j̅ + 3k̅
Now \([\overline{\mathrm{AB}} \overline{\mathrm{AC}} \overline{\mathrm{AD}}]=\left|\begin{array}{ccc}
-4 & -6 & -2 \\
-1 & 4 & 3 \\
-8 & -1 & 3
\end{array}\right|\)
= -4(15) + 6(21) – 2(33)
= -60 + 126 – 66
= 126 – 126
= 0
∴ The vectors AB, AC, AD are coplanar.
∴ The four points A, B, C and D are coplanar.
![]()
Question 17.
If a̅ = 2i̅ + j̅ – k̅, b̅ = – i̅ + 2j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅, then find (a̅ × b̅).(b̅ × c̅). [Mar. ’19(AP); Mar. ’17(TS)]
Answer:
Given a̅ = 2 i̅ + j̅ – k̅; b̅ = – i̅ + 2j̅ – 4k̅; c̅ = i̅ + j̅ + k̅
Now a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 1 & -1 \\
-1 & 2 & -4
\end{array}\right|\)
= i̅ (-4 + 2) – j̅ (-8 – 1) + k̅ (4 + 1)
= -2i̅ + 9j̅ + 5k̅
b̅ × c̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
-1 & 2 & -4 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (2 + 4) – j̅ (-1 + 4) + k̅ (-1 – 2)
= 6i̅ – 3j̅ – 3k̅
(a̅ × b̅).(b̅× c̅) = (-2i̅ + 9j̅ + 5k̅ ).(6i̅ – 3j̅ – 3k̅) = -12 – 27 – 15 = -54