TS Inter 1st Year Maths 1A Product of Vectors Important Questions Very Short Answer Type

Students must practice these Maths 1A Important Questions TS Inter 1st Year Maths 1A Product of Vectors Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1A Product of Vectors Important Questions Very Short Answer Type

Question 1.
Find the angle between the vectors i̅ + 2j̅ + 3k̅ and 3i̅ – j̅ + 2k̅. [Mar. ’17(TS), ’14, ’10] [Mar. ’18(AP)]
Answer:
Let a̅ = i̅ + 2 j̅ + 3k̅ and b̅ = 3i̅ – j̅ + 2k̅

Let θ be the angle between the vectors a and b then cos θ = \(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}||\bar{b}|}\)

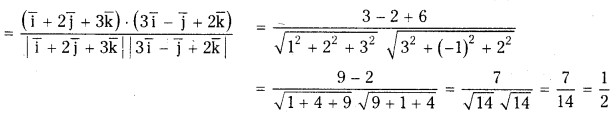
∴ θ = 60°

If a̅ = 6i̅ + 2j̅ + 3k̅ and b̅ = 2i̅ – 9j̅ + 6k̅ then find a̅. b̅ and the angle between a̅ and b̅. [Mar ’98]
Answer:
12, cos^-1\(\left(\frac{12}{77}\right)\)

Question 2.
If a̅ = i̅ + 2j̅ – 3k̅ and b̅ = 3i̅ – j̅ + 2k̅, then show that a̅ + b̅ and a̅ – b̅ are perpendicular to each other. [Mar. ’15(AP); Mar ’11; Mar. ’10, ’08; B.P]
Answer:
Given vectors are a̅ = i̅ + 2j̅ – 3k̅ and b̅ = 3i̅ – j̅ + 2k̅
Now a̅ + b̅ = i̅ + 2j̅ – 3k̅ + 3i̅ – j̅ + 2k̅ = 4i̅ + j̅ – k̅
a̅ – b̅ = i̅ + 2j̅ – 3k̅ – 3i̅ + j̅ – 2k̅ = -2i̅ + 3j̅ – 5k̅
Now, (a̅ + b̅) . (a̅ – b̅) = (4i̅ + j̅ – k̅) . (-2i̅ + 3 j̅ – 5k̅)
= -8 + 3 + 5 = -8 + 8 = 0
∴ a̅ + b̅ and a̅ – b̅ are perpendicular to each other.

Question 3.
Let a̅ and b̅ be non – zero, non-collinear vectors. If |a̅ + b̅| = |a̅ – b̅| then find the angle between a̅ and b̅. [Mar. ’94]
Answer:
Given |a̅ + b̅| = |a̅ – b̅|
Squaring on both sides ⇒ |a̅ + b̅|² = |a̅ – b̅|²
⇒ a̅² + b̅² + 2a̅. b̅ = a̅² + b̅² – 2a̅.b̅
⇒ 4a̅.b̅ = 0
⇒ a̅.b̅ = 0
∴ Angle between a̅ and b̅ is 90°.

Question 4.
If the vectors 2i̅ + λj̅ – k̅ and 4i̅ – 2j̅ + 2k̅ are perpendicular to each other, then find λ. [Mar ’15(TS); May ’05; Mar. ’05]
Answer:
Let a̅ = 2i̅ + λj̅ – k̅; b̅ = 4i̅ – 2j̅ + 2k̅
Since the vectors a and b are perpendicular, then a̅ . b̅ = 0
(2i̅ + λj̅ – k̅) . (4i̅ – 2j̅ + 2k̅) = 0
8 – 2λ – 2 = 0
6 – 2λ = 0
⇒ 2λ = 6
⇒ λ = 3

For what values of λ, the vectors i̅ – λj̅ + 2k̅ and 8i̅ + 6 j̅ – k̅ are at right angles ?
Answer:
1

If the vectors λi̅ – 3j̅ + 5k̅ and 2λi̅ – λj̅ – k̅ are perpendicular to each other then find λ. [Mar. ’19(AP); Mar ’16(TS); May ’14]
Answer:
\(\frac{-5}{2}\) or 1.

Question 5.
Let a̅ = i̅ + j̅ + k̅ and b̅ = 2i̅ + 3j̅ + k̅, find projection vector of b̅ on a̅ and its magnitude.
Answer:
Orthogonal projection of vector b̅ on a̅ is
= \(\frac{(\bar{a} \cdot \bar{b}) \bar{a}}{|\bar{a}|^2}=\frac{[(\bar{i}+\bar{j}+\bar{k}) \cdot(2 \bar{i}+3 \bar{j}+\bar{k})]}{|\bar{i}+\bar{j}+\bar{k}|^2}\)
= \(\frac{(2+3+1)}{(\sqrt{3})^2}\)(i̅ + j̅ + k̅) = 2(i̅ + j̅ + k̅)
Magnitude = |2(i̅ + j̅ + k̅)| = 2\(\sqrt{1+1+1}\) = 2√3

If a̅ = i̅ – j̅ – k̅ and b̅ = 2i̅ – 3j̅ + k̅, then find the projection vector of b̅ on a̅ and its magnitude. [Mar ’17(AP), ’91]
Answer:
\(\frac{4}{3}\)(i̅ – j̅ – k̅); \(\frac{4}{\sqrt{3}}\)

Question 6.
If a̅ = 2i̅ + 2j̅ – 3k̅, b̅ = 3i̅ – j̅ + 2k̅, then find the angle between the vectors 2a̅ + b̅ and a̅ + 2b̅. [Mar ’02; Mar. ’02]
Answer:
Given that a̅ = 2i̅ + 2j̅ – 3k̅, b̅ = 3i̅ – j̅ + 2k̅
Now, 2a̅ + b̅ = 2(2i̅ + 2 j̅ – 3k̅) + 3i̅ – j̅ + 2k̅
= 7i̅ + 3 j̅ – 4k̅
a̅ + 2b̅ = 2i̅ + 2j̅ – 3k̅ + 2(3i̅ – j̅ + 2k̅)
= 8i̅ + k̅
If θ is the angle between 2a̅ + b̅ and a̅ + 2b̅ then

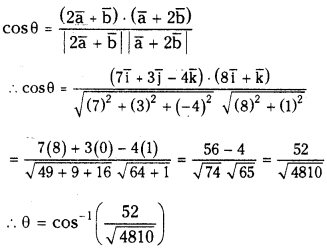
Question 7.
If a̅ = 2i – j̅ + k̅ and b̅ = i̅ – 3j̅ – 5k̅, then find a̅ × b̅. [Mar. ’13]
Answer:
a̅ = 2 i̅ – j̅ + k̅ and b̅ = i̅ – 3j̅ – 5k̅

a̅ × b̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & -1 & 1 \\
1 & -3 & -5
\end{array}\right|\) = i̅ (5 + 3) – j̅ (-10 -1) + k̅ (- 6 +1) = 8i̅ +11j̅ – 5k̅
∴ |a̅ × b̅| = \(\sqrt{64+121+25}=\sqrt{210}\)

Question 8.
If 4i̅ + \(\frac{2p}{3}\) j̅ + pk̅ is parallel to vector i̅ + 2j̅ + 3k̅, find p.
Answer:
Let a̅ = 4i̅ + \(\frac{2p}{3}\) j̅ + pk̅, b̅ = i̅ + 2j̅ + 3k̅
Since the vector a̅ and b̅ are parallel then
⇒ \(\frac{4}{1}=\frac{2 p / 3}{2}=\frac{p}{3}\)
⇒ 4 = \(\frac{\mathrm{p}}{3}=\frac{\mathrm{p}}{3} \Rightarrow \frac{\mathrm{p}}{3}\) = 4
⇒ p = 12

Question 9.
Find the area of the parallelogram having a̅ = 2j̅ – k̅ and b̅ = -i̅ + k̅ as adjacent sides.
Answer:
Given a̅ = 2j̅ – k̅, b̅ = -i̅ + k̅
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
0 & 2 & -1 \\
-1 & 0 & 1
\end{array}\right|\)
= i̅(2 – 0) – j̅(0 – 1) + k̅(0 + 2)
= 2i̅ + j̅ + 2k̅
|a̅ × b̅| = \(\sqrt{(2)^2+(1)^2+(2)^2}=\sqrt{4+1+4}=\sqrt{9}\) = 3
∴ The area of the parallelogram having a̅ and b̅ as adjacent sides = |a̅ × b̅| = 3 sq.units.

Find the area of the parallelogram for which the vectors a̅ = 2i̅ – 3j̅ and b̅ = 3i̅ – k̅ are adjacent sides. [Mar. ’12, ’08, ’07; Mar. ’08]
Answer:
\(\sqrt{94}\) sq. units.

Question 10.
Find the area of the parallelogram whose diagonals are 3i̅ + j̅ – 2k̅ and i̅ – 3j̅ + 4k̅. [May ’02]
Answer:
Let a̅ = 3i̅ + j̅ – 2k̅ & b̅ = i̅ – 3j̅ + 4k̅
a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
3 & 1 & -2 \\
1 & -3 & 4
\end{array}\right|\)
= i̅(4 – 6) – j̅(12 + 2) + k̅(-9 – 1) = -2i̅ – 14j̅ – 10k̅
|a̅ × b̅| = \(\sqrt{(-2)^2+(-14)^2+(-10)^2}\)
= \(\sqrt{4+196+100}\)
= \(\sqrt{300}\) = 10√3

The area of the parallelogram whose diagonals a̅ and b̅ is
\(\frac{1}{2}\)|a̅ × b̅| = \(\frac{1}{2}\) × 10√3 = 5√3 sq.units

Question 11.
W Find unit vector perpendicular to the plane determined by the vectors a̅ = 4i̅ + 3j̅ – k̅ and b̅ = 2i̅ – 6j̅ – 3k̅.
Answer:
Given vectors are a̅ = 4i̅ + 3j̅ – k̅ and b̅ = 2i̅ – 6j̅ – 3k̅
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
4 & 3 & -1 \\
2 & -6 & -3
\end{array}\right|\)
= i̅(-9 – 6) – j̅(-12 + 2) + k̅(-24 – 6) = -15i̅ + 10j̅ – 30k̅

|a̅ × b̅| = \(\sqrt{(-15)^2+(10)^2+(-30)^2}\)
= \(\sqrt{225+100+900}=\sqrt{1225}\) = 35
∴ The unit vector perpendicular to the plane determined by the vector a̅ and b̅ = \(\pm \frac{(\bar{a} \times \bar{b})}{|\bar{a} \times \bar{b}|}\)
= \(\pm \frac{(-15 \overline{\mathrm{i}}+10 \overline{\mathrm{j}}-30 \overline{\mathrm{k}})}{35}=\pm \frac{(-3 \overline{\mathrm{i}}+2 \overline{\mathrm{j}}-6 \overline{\mathrm{k}})}{7}\)

If a̅ = 2i̅ – 3j̅ + 5k̅, b̅ = -i̅+ 4j̅ + 2k̅ then find a̅ x b̅ and unit vector perpendicular to both a̅ and b̅.
Answer:
\(\pm\left(\frac{1}{\sqrt{782}}\right)\)(-26i̅ – 9j̅ + 5k̅)

Find unit vector perpendicular to both i̅ + j̅ + k̅ and 2i̅ + j̅ + 3k̅.
Answer:
\(\pm \frac{1}{\sqrt{6}}\)(2i̅ – j̅ – k̅)

Question 12.
Let a̅ = 2i̅ – j̅ + k̅ and b̅ = 3i̅ + 4j̅ – k̅. If θ is the angle between a̅ and b̅, then find sin θ.
Answer:
Given a̅ = 2i̅ – j̅ + k̅ and b̅ = 3i̅ + 4j̅ – k̅

Question 13.
Compute [i̅ – j̅ j̅ – k̅ k̅ – i̅] [Mar ;’96; Mar. ’95]
Answer:
[i̅ – j̅ j̅ – k̅ k̅ – i̅] = \(\left|\begin{array}{rrr}
1 & -1 & 0 \\
0 & 1 & -1 \\
-1 & 0 & 1
\end{array}\right|\) = 1(1 – 0) + 1(0 – 1) + 0(0 + 1)
= 1(1) + 1(-1) + 0(1) = 1 – 1 = 0

Question 14.
If a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅ then compute a̅.(b̅ × c̅). [May ’08]
Answer:
Given a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅ then
a̅.(b̅ × c̅) = [a̅ b̅ c̅] = \(\left|\begin{array}{ccc}
1 & -2 & -3 \\
2 & 1 & -1 \\
1 & 3 & -2
\end{array}\right|\)
= 1(-2 + 3) + 2(-4 – 1) – 3(6 – 1) = 1 – 6 – 13 = -20

If a̅ = (1, -1, -6), b̅ = (1, -3, 4) and c̅ = (2, -5, 3), then compute a̅.(b̅ × c̅).
Answer:
0

Question 15.
Find the volume of the parallelopiped having coterminus edges i̅ + j̅ + k̅, i̅ – j̅ and i̅ + 2j̅ – k̅. [May ‘09; Mar. ‘03]
Answer:
Let a̅ = i̅ + j̅ + k̅,
b̅ = i̅ – j̅
and c̅ = i̅ + 2j̅ – k̅
The volume of parallelopiped having coterminus edges a̅, b̅, c̅ is = [a̅ b̅ c̅]
= \(\left|\begin{array}{rrr}
1 & 1 & 1 \\
1 & -1 & 0 \\
1 & 2 & -1
\end{array}\right|\)
= 1(1 – 0) – 1(-1 – 0) + 1(2 + 1)
= 1(1) – 1(-1) + 1(3)
= 1 + 1 + 3
= 5 cubic units.

Find the volume of the parallelopiped whose coterminus edges are represented by the vectors 2i̅ – 3j̅ + k̅, i̅ – j̅ + 2k̅ and 2i̅ + j̅ – k̅.
Answer:
14 cubic units.

Question 16.
For non coplanar vectors a̅, b̅ and c̅, determine p for which the vectors a̅ + b̅ + c̅, a̅ + pb̅ + 2c̅ and -a̅ + b̅ + c̅ are coplanar. [May ’01]
Answer:
Given a̅, b̅, c̅ are non coplanar vector we have [a̅ b̅ c̅] ≠ 0
If the vectors a̅ + b̅ + c̅, a̅ + pb̅ + 2c̅ and -a̅ + b̅ + c̅ are coplanar
Then [a̅ b̅ c̅]\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & p & 2 \\
-1 & 1 & 1
\end{array}\right|\) = 0
\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & p & 2 \\
-1 & 1 & 1
\end{array}\right|\) = 0 (∵ [a̅ b̅ c̅] ≠ 0)
⇒ 1(p – 2) – 1(1 + 2) + 1(1 + p) = 0
⇒ p – 2 – 3 + 1 + p = 0
⇒ 2p – 4 = 0
⇒ 2p = 4
⇒ p = 2

Find ‘t’ for which the vectors 2i̅ – 3j̅ + k̅, i̅ + 2j̅ – 3k̅ and j̅ – tk̅ are coplanar.
Answer:
1

If the vector a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ + 2j̅ – 3k̅ and c̅ = 3i̅ + pj̅ + 5k̅ are coplanar then find p.
Answer:
-4.

Question 17.
Determine λ for which the volume of the parallelopiped having coterminus edge; i̅ + j̅, 3i̅ – j̅ and 3j̅+ λk̅ is 16 cubic units. [May
Answer:
Let a̅ = i̅ + j̅, b̅ = 3i̅ – j̅ and c̅ = 3j̅+ λk̅
The volume of the parallelopiped having coterminus edges a̅, b̅, c̅ is [a̅ b̅ c̅]
Given that the volume of the parallelopiped = ± 6
[a̅ b̅ c̅] = ±6 = \(\left|\begin{array}{rrr}
1 & 1 & 0 \\
3 & -1 & 0 \\
0 & 3 & \lambda
\end{array}\right|\) =±16
⇒ 1(-λ -0) -1(3λ – 0) + 0(9 – 0) = ± 16
⇒ -λ – 3λ + 0 = ± 16
⇒ -4λ =± 16
⇒ λ = ±4

Question 18.
Show that i̅ × (a̅ × i̅) + j̅ × (a̅ × j̅) + k̅ × (a̅ × k̅) = 2a̅ for any vector a̅. [Mar. ’03; May ’98]
Answer:
Let a = xi̅ + yj̅ + zk̅
Now i̅ × (a̅ × i̅) = (i̅.i̅)a̅ – (i̅.a̅)i̅ = a̅ – (i̅.a̅)i̅;
j̅ × (a̅ × j̅) = a̅ – (j̅.a̅)j̅;
k̅ ×(a̅ × k̅) = a̅ – (k̅.a̅)k̅

LHS = i̅ x (a̅ x i̅) + j̅ x (a̅ x j̅) + k̅ x (a̅ x k̅)
= a̅ – (i̅.a̅)i̅ + a̅ – (j̅ . a̅)j̅ + a̅ – (k̅ . a̅)k̅
= 3a̅ – [(i̅.a̅)i̅ +(j̅.a̅)j̅ + (k̅.a̅)k̅]
= 3a̅ – [(x)i̅ + (y)j̅ (z)k̅]
= 3a̅ – a̅ = 2a̅
= RHS

Question 19.
For any three vectors a̅, b̅, c̅ , prove that [b̅ + c̅ c̅ + a̅ a̅ + b̅] = 2[a̅ b̅ c̅]. [Mar. ’00, ’99]
Answer:
LHS = [b̅ + c̅ c̅ + a̅ a̅ + b̅]
= [a̅ b̅ c̅]\(\left|\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right|\) = [a̅ b̅ c̅][0(0 – 1) – 1(0 – 1) + 1 (1 – 0)]
= [a̅ b̅ c̅][0 + 1 + 1] = 2[a̅ b̅ c̅] = R.H.S

Question 20.
For any three vectors a̅, b̅, c̅, prove that [b̅ × c̅ c̅ × a̅ a̅ × b̅] = [a̅ b̅ c̅]². [May ’02, ’98]
Answer:
LHS = [b̅ × c̅ c̅ × a̅ a̅ × b̅] = (b̅ × c̅).[(c̅ × a̅) × (a̅ × b̅)]
= (b̅ × c̅).[{(c̅ × a̅).b̅}a̅ – {(c̅ × a̅). a̅}b̅]
= (b̅ × c̅).a̅[c̅ a̅ b̅] = [a̅ b̅ c̅][a̅ b̅ c̅] = [a̅ b̅ c̅]² = RHS